Применение средств алгебры логики для описания функционирования устройств компьютера

Для описания того, как функционируют аппаратные средства компьютера очень удобен математический аппарат алгебры логики, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры «1» и «0».

Одни и те же устройства компьютера могут применяться для обработки и хранения числовой информации, представленной в двоичной системе счисления, логических переменных. На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.

Данные и команды в памяти компьютера и в регистрах процессора представляются в виде двоичных последовательностей различной структуры и длины.

Существуют различные физические способы кодирования двоичной информации, но чаще всего единица кодируется более высоким уровнем напряжения, чем ноль.

В логической схеме компьютера выделяют логические элементы. Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую формулу.

Логическими элементами компьютеров являются электронные схемы «И», «ИЛИ», «НЕ», «И-НЕ», «ИЛИ-НЕ» и другие (называемые также вентилями), а также триггер. С помощью этих схем можно реализовать любую логическую формулу, описывающую работу устройств компьютера.

Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую формулу, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.

Схема «И» реализует конъюнкцию двух или более логических значений. Условное обозначение на структурных схемах схемы «И» с двумя входами представлено на рис. 5.

Рис. 5. схема «И»

На выходе схемы «И» значение «1» будет тогда и только тогда, когда на всех входах будут «1». Когда хотя бы на одном входе будет «0», на выходе также будет «0».

Операция конъюнкции на функциональных схемах обозначается знаком «&» (читается как «амперсэнд»), являющимся сокращенной записью английского слова and.

Схема «ИЛИ» реализует дизъюнкцию двух или более логических значений. Условное обозначение схемы «ИЛИ» представлено на рис. 6.

Рис. 6. Схема «ИЛИ»

Значение дизъюнкции равно «1», если сумма значений операндов больше или равна «1». Когда хотя бы на одном входе схемы «ИЛИ» будет «1», на её выходе также будет «1».

Операция дизъюнкции на функциональных схемах обозначается знаком «1».

Схема «НЕ» (инвертор) реализует операцию отрицания. Условное обозначение схемы НЕ представлено на рис. 7.

Рис. 7. Схема «НЕ»

Если на входе схемы – «0», то на выходе будет «1». Когда на входе – «1», на выходе будет «0».

Схема «И-НЕ» состоит из элемента «И» и инвертора и осуществляет отрицание результата схемы «И». Условное обозначение схемы «И-НЕ» представлено на рисунке 8. Таблица истинности схемы «И-НЕ» – это таблица 5.

Рис. 8. Схема «И-НЕ»

Таблица истинности схемы «И-НЕ»

Таблица 5

х	у

Схема «ИЛИ-НЕ» состоит из элемента «ИЛИ» и инвертора и осуществляет отрицание результата схемы «ИЛИ». Условное обозначение схемы «ИЛИ-НЕ» представлено на рис. 9, а таблица истинности схемы ИЛИ-НЕ – это табл. 6.

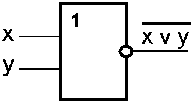
Рис. 9. Схема «ИЛИ-НЕ»

Таблица истинности схемы «ИЛИ-НЕ»

Таблица 6

х	у

Логические схемы

Логическая схема – это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.

Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале).

Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей.

При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.

СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим трём этапам:

1. составлению функции проводимости по таблице истинности, отражающей эти условия;
2. упрощению этой функции;
3. построению соответствующей схемы.

АНАЛИЗ СХЕМЫ сводится к:

1. определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных.
2. получению упрощённой формулы.

Пример решение логических задач средствами алгебры логики

Задача: Составить таблицу истинности для данной формулы: (x ~ z) | ((x y) ~ (y z)).

Решение: В таблицу истинности данной формулы полезно включить таблицы истинности промежуточных функций:

Поиск по сайту: