 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Эквиваленция (равнозначность)
Результатом операции эквиваленции для высказывания А ~ В будет истинна тогда, когда истинны или ложны одновременно оба высказывания. Отличие эквиваленции от конъюнкции состоит в том, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания. Пример 14. Высказывания А = «2 + 2 = 7» и В = «1 – 8 = 5». Сложное высказывание А º В (А ~ В) истинно, так как оба высказывания ложны.
Импликация Результатом операции импликации для высказывания А ® В будет ложь только тогда, когда первое высказывание (А) истинно, а второе (В) ложно. При этом А – предпосылка, а В – следствие. Пример 15. Высказывания А = «2 + 2 = 4» и В = «1 – 8 = 5». Сложное высказывание А ® В (А Þ В) ложно, так как высказывание А истинно, а В – ложно. Антиконъюнкция Результатом операции антиконъюнкции для высказывания А ½ В будет ложь только тогда, когда оба высказывания истинны. Пример 16. Высказывания А= «Москва – столица России» и В= «Рим – столица Италии». Сложное высказывание А ½ В ложно, так как истинны оба высказывания. Антидизъюнкция Результатом операции антидизъюнкции для высказывания А ¯ В будет истинна только тогда, когда оба высказывания ложны. Пример 17. Высказывания А= «Рим – столица России» и В= «Москва – столица Италии». Сложное высказывание А ¯ В истинно, так как ложны оба высказывания. Основными символами алгебры логики являются:
Переменная, значениями которой являются высказывания, называется пропозициональной переменной. Далее индуктивно вводится понятие формулы, являющееся формализацией понятия «сложного» высказывания. К формуле алгебры логики относят:
Правила сокращения записей в пропозициональных формулах:
~ ® Ú Ù Ø
Пример 18.
Для преобразований формул в равные формулы важную роль в алгебре логики играют следующие равенства:
Эти равенства позволяют существенно упростить запись формул освобождением от лишних скобок.
Нормальные формы Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые. Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причём среди переменных могут быть одинаковые.
Поиск по сайту: |
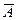 ;
;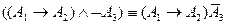 ;
;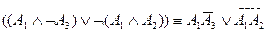 .
.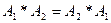 (закон коммутативности).
(закон коммутативности).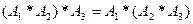 (закон ассоциативности).
(закон ассоциативности).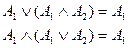 (закон поглощения).
(закон поглощения). (закон дистрибутивности).
(закон дистрибутивности).
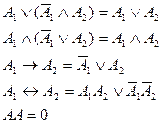 (закон противоречия).
(закон противоречия).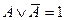 (закон исключенного третьего);
(закон исключенного третьего); (закон снятия двойного отрицания);
(закон снятия двойного отрицания);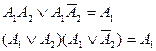 (закон склеивания);
(закон склеивания);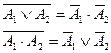 (закон де Моргана);
(закон де Моргана);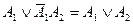 (закон свертки).
(закон свертки).