 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
У СТАТИЧНО ВИЗНАЧЕНИХ РАМАХ ⇐ ПредыдущаяСтр 4 из 4
Під дією зовнішнього навантаження, температурного поля і в результаті зсуву опор споруда деформується, а її точки переміщуються. У будівельній механіці прийнято переміщення будь-якого вигляду позначати символом Перший індекс “і” вказує на номер переміщення. Це число можна використовувати і для позначень напрямку переміщення. Другий індекс “k” вказує на номер завантаження, яке викликає переміщення. Розглянемо, як приклад, балку, на яку діє декілька зовнішніх впливів (рис. 4.1).
Рис.4.1
Припустимо, що нас цікавлять наступні переміщення точок балки: - вертикальне переміщення в точці А; - кут повороту осі в точці А; - кут повороту осі в точці В; - вертикальне переміщення в точці К. Пронумеруємо вказані переміщення. Ці номери на рис.4.1 позначені в лапках. Нехай на балку діють незалежно три групи навантажень 1, 2, 3. Тоді вертикальне переміщення точки А, викликане навантаженням Для позначення вигляду і напрямку переміщінь, як правило, використовують допоміжні стани рами. У цих станах за напрямком визначення переміщення прикладається одинична сила. У цьому випадку величина Отже, для визначення переміщення в рамі необхідно мати два її стани. Один стан “к”, який зумовлений дією зовнішніх навантажень (рис.4.2,а), і другий стан “і” , який називається допоміжним або одиничним і отримується якщо прикласти до рами одиничну узагальнену безрозмірну силу за напрямком шуканого переміщення (рис. 4.2,б-е). Ця сила може являти собою зосереджену силу, зосереджений момент або групу зосереджених сил або моментів . Коли потрібно визначити взаємний кут повороту двох перерізів, то в цих перерізах потрібно прикласти два протилежні за знаком моменти М=1. На рис. 4.2 наведені допоміжні стани при визначенні наступних переміщень для рами: вертикального для точки А (∆1к) - (рис. 4.2.б); горизонтального для точки В (∆2к) - (рис. 4.2,в); взаємного зближення точок С і Д (∆3к) - (рис. 4.2,г); кута повороту перерізу на опорі Е (∆4к) – (рис. 4.2,д); взаємного кута повороту перерізів, розташованих зліва і справа шарніру А (∆5к) – (рис. 4.2, е).
Рис. 4.2
Одиничні сили у допоміжному стані можна скерувати як завгодно (вверх чи вниз, вліво чи вправо, за чи проти годинникової стрілки). Коли підрахунки дадуть знак «плюс», то це буде означати, що переміщення збігається із вибраним попередньо напрямком одиничної сили; у разі від’ємного результату переміщення скероване у протилежнипй бік. Величина
Тут При обчисленні переміщень за (4.1) у стержневих системах, що складаються з прямих стержнів, поперечні перетини яких є сталі, характеристики перетинів можуть бути винесені за знак інтеграла, а під інтегралом залишається добуток двох функцій
Для обчислення цього інтеграла використовують формулу Сімпсона або правило Верещагіна. Якщо одна з епюр (
При розрахунку інтеграла достатньо знати крайні і середні ординати добуткових епюр. Добуток ординат в (4.3) додатній, якщо ординати епюр Якщо епюри в межах довжини стержня мають стрибок або злам, то в межах цього стержня необхідно використовувати формулу Сімпсона для кожної ділянки окремо.
Визначення інтеграла за правилом Верещагіна може бути використано у тому випадку, коли одна із епюр лінійна, а інша може бути довільною (лінійною, криволінійною або ламаною). За правилом Верещагіна інтеграл (4.2) дорівнює добутку площі криволінійної епюри на ординату другої фігури, розташовану під центром ваги площі першої епюри (рис.4.4).
При перемноженні за правилом Верещагіна, двох лінійних епюр у формулі (4.4) площу можна брати будь-якої епюри. Правило Верещагіна використовується у тих випадках, коли достатньо легко визначити площу та положення центру ваги епюри. Найбільш зручно використовувати правило Верещагіна при перемноженні трикутних і прямокутних епюр. У формулі (4.4) добуток У таблиці 4.1 подано площі та абсциси центрів ваги епюр, які найчастіше зустрічаються.
Таблиця 4.1.
Отже, дпя обчислення переміщення в заданій рамі, що знаходиться під дією навантаження необхідно: - визначити згинаючі моменти - вибрати допоміжний стан “і”, завантаживши раму одиничною безрозмірною силою по напрямку шуканого переміщення; - визначити опорні реакції - обчислити переміщення Порядок визначення переміщень рами від зовнішнього навантаження проілюструємо на окремих прикладах.
Приклад 8. Для рами на рисунку 4.5,а визначити кут повороту перетину, розташованого безпосередньо близько до опори В.
Рис. 4.5
Для шуканого переміщення вибираємо допоміжний стан (рис.4.5,б). На рис.4.5,в і 4.5,г зображені епюри згинальних моментів у заданому і допоміжному стані рами. Для визначення переміщення використовуємо формулу (4.1)
Інтеграли у межах стояка і ригеля обчислюємо за формулою Сімпсона (4.3) та за формулою Верещагіна (4.4)
Приклад 9. Визначити взаємне зміщення точок C і В (позначимо його Δ1р ) для рами, наведеної на рис.4.6.
Рис. 4.6
Взаємне зміщення точок С і В є узагальненим переміщенням. У допоміжному стані прикладаємо узагальнену силу Р1=1. У даному випадку узагальнена сила складається з двох сил, прикладених у точках С і В по напрямку СВ (рис.4.6,б). Епюри заданого і допоміжного стану показані на рис.4.6, в і 4.6, г. Переміщення Δ1р можна отримати використовуючи спосіб Верещагіна.
Поиск по сайту: |
 з двома індексами, наприклад
з двома індексами, наприклад  .
.
 та
та  , буде позначено
, буде позначено  ; вертикальне переміщення точки К, викликане навантаженями
; вертикальне переміщення точки К, викликане навантаженями 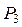 та
та  , буде позначено
, буде позначено  , кут повороту осі в точці В, викликане навантаженями
, кут повороту осі в точці В, викликане навантаженями  та
та  , буде позначено
, буде позначено  і т.д.
і т.д. означає переміщення за напрямком сил допоміжного одиничниго стану “і” від дії сил стану “к”, що вважається дійсним.
означає переміщення за напрямком сил допоміжного одиничниго стану “і” від дії сил стану “к”, що вважається дійсним.






 переміщення, яке викликане дією зовнішніх сил визначається за формулою Максвелла-Мора, яка для балок та рам має спрощений вигляд:
переміщення, яке викликане дією зовнішніх сил визначається за формулою Максвелла-Мора, яка для балок та рам має спрощений вигляд: .
.
 та
та  - згинаючі моменти у допоміжному стані від дії одиничної сили і у заданому стані від дії зовнішнього навантаження,
- згинаючі моменти у допоміжному стані від дії одиничної сили і у заданому стані від дії зовнішнього навантаження,  - жорсткість стержня на згин;
- жорсткість стержня на згин;  - довжина ділянки.
- довжина ділянки. та
та  :
:
 ) окреслюється квадратною параболою, а друга (
) окреслюється квадратною параболою, а друга ( 
 та
та  відкладені по одну сторону стержня.
відкладені по одну сторону стержня.


 та
та  додатній, якщо центр ваги епюри
додатній, якщо центр ваги епюри  епюри
епюри  розташовані по одну сторону від осі стержня (так як, наприклад, на рис.4.4).
розташовані по одну сторону від осі стержня (так як, наприклад, на рис.4.4).
















 в стержнях рами від зовнішнього навантаження;
в стержнях рами від зовнішнього навантаження; і внутрішні зусилля
і внутрішні зусилля  та
та  у допоміжному стані;
у допоміжному стані; від дії зовнішнього навантаження за формулою (4.1). Інтегрування виконати або за правилом Верещагіна (4.4) або за формулою Сімпсона (4.3). Додатній знак результату вкаже, що напрямок переміщень співпадає з напрямом одиничної сили допоміжного стану. Від`ємний результат буде доказом того, що насправді напрямок переміщення протилежний до напрямку сили допоміжного стану.
від дії зовнішнього навантаження за формулою (4.1). Інтегрування виконати або за правилом Верещагіна (4.4) або за формулою Сімпсона (4.3). Додатній знак результату вкаже, що напрямок переміщень співпадає з напрямом одиничної сили допоміжного стану. Від`ємний результат буде доказом того, що насправді напрямок переміщення протилежний до напрямку сили допоміжного стану.
 .
.

 (м).
(м).