 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Основные свойства сжимающих отображений ⇐ ПредыдущаяСтр 6 из 6
Теорема 2. Любое сжимающее отображение f метрического пространства Х в себя – непрерывное на множестве Х. 3Возмьмём произвольно точку хоÎХ и докажем, что f – непрерывное на Х, т.е.
Из неравенства (1) следует, что rx( f(xo),f(x))£ arx(xo,x) < a×e/a = e. Отображение f непрерывное на множестве Х, т.к. оно непрерывное в любй точке хо этого множества. 4 Теорема 3.( принцип сжимающих отображений Баноха).Любое сжимающее отображение полного метрического пространства (Х, r) в себя (f: Х ® Х) имеет неподвижную точку и при том только одну. (Х ≠ 31.Выбярэм любы точка хо ÎХ и пабудуем последовательность (хn) па правилу: (2) 2. Докажем, что последовательность (xn) фундаментальная, т.е. "e>0 $N½"n,m > N Þ r(xm,xn)<e. Обозначим r(x1,xо)=d. (3) По условию теоремы f – сжимающее отображение. Воспользуемся неравенством (1) и обозначением (3).Получим:
Используя метод математической индукции, можно доказать, что (4) Возьмём произвольно натуральные числа m и n (m>n)и оценим r(xm, xn), используя неравенство треугольника и неравенство (4).Получим:
Т.к. 0 < a < 1, то an + an+1 +…+ am - сумма n-членов бесконечно ўбывающей геометрической прогрессии. Поэтому r(xn, xm) £ d Предел последовательности (6) Из неравенств (5) и (6) следует r(xn, xm)<e. Т.обр. показали, что "e>0$NÎN ½"n,m > N Þ r(xm,xn)<e.Þ последовательность (2) фундаментальная. 3.Покажем, что последовательность (2) стремится к точке По условию теоремы (Х, r) - полное метрическое пространство, (хn)– любая его фундаментальная последовательность и она должна сходиться к элементу пространства (Х, r), а значит. существует точка
4.Докажем, что Из равенства (7) следует, что В силу теоремы 2 любое сжимающее отображение – непрерывное. Поэтому С учётом (8), доказана неподвижность точки 5.Докажем единственность неподвижной точки. Пусть есть ещё одна неподвижная точка х*. Таким образом существуют две точки
Но это произведение может быть тольки неотрицательным (т.к. r( Замечание. Метод нахождения неподвижных точек называется методом итерации, или методом последовательных приближений. Этот метод используют при доказательстве единственности решения некоторых алгебраических и дифференциальных уравнений. Пример 1.Пусть f – фукция - отображение отрезка [a,b] в отрезок [a,b], задана формулой f(x) = y (9) Эта фукция дифференцируемая, и её производная удовлетворяет неравенству: ½f’(x)½£ a (0 < a < 1) "x Î[a,b]. Докажем, что уравнение f(x) = x (9). имеет единственное решение. 3[a,b]– замкнутое множество полным метрическим пространством Rи поэтому подпространство Х = ([a,b] , r(x,y) = ½х-у½) - полное метрическое пространство. Фукция f удовлетворяет условиям теоремы Логранжа на [a,b] :
По определению 3 f – сжимающее отображение полного метрического пространства в себя. По теореме Баноха существует единственная точка
Поиск по сайту: |
 )
) (5)
(5)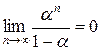 , а это значит, что последовательность
, а это значит, что последовательность  – бесконечно малая, и (по определению БМП)
– бесконечно малая, и (по определению БМП) ÎХ.
ÎХ. (7)
(7) а согласно равенствам (2) f(xn-1) = xn. Значит
а согласно равенствам (2) f(xn-1) = xn. Значит  (8)
(8)