 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение и примеры метрических пространствСтр 1 из 6Следующая ⇒
ГЛАВА ОСНОВНЫЕ СТРУКТУРЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА Определение и примеры метрических пространств Будем обозначать расстояние между двумя точками М1 и М2 символом
и обладает свойствами: 1) r(M1,M2)³ 0; причём r(M1,M2) = 0 Û M1 = M2; 2) r(M1,M2) = r(M2,M1); 3)r(M1,M2) £ r(M1,M3) + r(M2,M3) (неравенство треугольника). Обобщим понятие расстояния на любое множество с помощью понятия метрики. Для этого нам понадобится понятие декартового произведения двух множеств: X ´ Х = Пусть Х – некоторое непустое множество любой природы. Рассмотрим декартовое произведение Определение 1. Метрикойна множестве Х называется действительная функтия двух переменных r, заданная на Х ´ Х и "x, y, zÎX,довлетворяющаяследующим условиям (аксиомам метрики): 1) r(x,y)³0; r(x,y)=0 Û x = y; 2) r(x,y) = r(y,x); 3) r(x,y) £ r(x,z) + r(y,z) (неравенство треугольника). Значение функтии r в точке (x,y), т.е. число r(x,y) называется расстояниеммежду точками x и y. Определение 2. Множество Х с заданной на нём метрикой r, т.е. пара(Х, r), называется метрическим пространством(м.пр.). Элементы множества Х называются элементами или точками м.пр. (Х, r). Пусть дано м.пр. (Х, r), и множество МÌХ, рассмотрим функтию rм(x,y)такую, что "x, y Î М значение rм(x,y) = r(x,y). Очевидно, что пара (М, rм )также является метрическим пространством.Пространство (М, rм) называется подпространством метрического пространства ( Х, r ). Замечание.Введенное понятие расстояния между точками метрического пространства позволяет рассмотреть важные вопросы о предельном переходе, непрерывности и диффернитируемости отображений и др. Примеры метрических пространств Пример 1. Пусть R – множество действительных чисел. Для любых чисел x,yÎR определим функтию r(x,y) = ½х- у½. (1) Очевидно, что (1) удовлетворяет аксиомам 1 и 2 метрики. Покажем, что функтия r удовлетворяет аксиоме 3 "x,y,zÎR : r(x,y) = ½х - у½= ½х- z + z- у½£ ½х - z½+ ½z - у½= r(x,z) + r(z,y). Пара (R, r), где r определяется равенством (1) – метрическое пространство, которое обозначают RилиR1. Пример 2. Множество М=[a,b] с метрикой r(x,y) = ½х- у½"x,yÎ[a,b]обозначают Х = ([a,b], r). Х – подпространство метрического пространстваR , т.к. [a,b]ÌR . Пример 3. Множество ратиональных чисел Q с метрикой, задаваемой формулай (1) для всех x, y ÎQ, является метрическим пространством. Пространство Х = (Q,r) – подпространство метрического пространства R и обозначается Q. Пример 4.Обозначим через Rm множество упорядоченных m –к действительных чисел .Элементы множестваRm называются векторами (точками) и обозначаются одной буквой х = (х1,х2,…, хm), y =(y1,y2 ,…, ym).числа х1, х2 ,…, хm – координаты вектора х. Элементы х и в равны между собой х = у, тогда и только тогда, когда х1 = у1, х2 = у2, …, хm = уm. На множестве Rm введем функтию
Покажем, что пространство (Rm ,r) = Rm,где r определяется равенством (2), является метрическим пространством. Легко убедится, что функтия r удовлетворяет первым двум аксиомам метрики. Для того, чтобы показать, что функтия удовлетворяет аксиоме 3, докажем 2 леммы. Лемма 1. Для любых действительных чисел ak , bk, k=1,2,…,m, верно неравенство Коши-Буняковского:
3Рассмотрим функтию
Так как квадратный трехчлен относительно t — неотрицательный, то его дискрименант — неположительный, т.е.
Лемма 2. Для любых действительных чисел ak ,bk , где k = 1,2,…,m верно неравенство Миньковского:
3
Покажем, что для функтии (2) выполняется аксиома 3. Возьмем любые три точки х = (х1, х2, …, хm), y = (y1, y2 , …, ym), z = (z1, z2, …, zm). Обозначим Подставив в неравенство (4) обозначения из (5), получим
Þ r(x,y) £ r(x,z) + r(z,y). 4 Пример 5. Рассмотрим множество Rm ,но теперь r зададим с помощью формулы
где х = (х1,х2,…, хm), y = (y1,y2 ,…, ym) – любые точки (векторы) пространства Rm.Докажем, что функтия (6) удовлетворяет аксиомам метрики. Функтия r удовлетворяет первым двум аксиомам метрики. Покажем, что функтия r удовлетворяет удовлетворяет аксиоме 3 для любых трех точек х = (х1,х2,…, хm), y = (y1,y2 ,…, ym), z = (z1,z2,…, zm)пространства Rm. 3 Þ r(x,y) £ r(x,z) + r(z,y). 4 Замечание. На одном и том же множестве можно разными способами задавать метрики. В результате будем получать разные метрические пространства. Пример 6. Рассмотрим множество С[a,b] всех действительных функций непрерывных на [a,b]. Для любых двух функций x(t) и y(t) из этого множества будем считать
Равенство (7) – чебышёвское расстояние между функтиями x(t) и у(t). Покажем, что функтия r(x,y)– метрика на множестве С[a,b]. Функтия r удовлетворяет первым двум аксиомам метрики. Покажем, что r удовлетворяет аксиоме 3. 3Пусть x, y, z Î С[a,b], где t Î[a,b]. Оценим модуль разности ½x(t) - y(t)½= ½x(t) - z(t) + z (t) - y(t)½£ ½x(t) - z(t)½+½z(t) - y(t)½£
Пример 7. Рассмотрим l2 – множество последовательностей действительных чисел (хÎ l2 , где х: х1, х2, ..., хn…), для которых сходится ряд
Так как ряд Функтия r, заданная формулой (9), удовлетворяет аксиомам 1 и 2 (очевидно). Докажем, что она удовлетворяет и аксиоме 3. 3Для любых трёх последовательностей x, y, z множества l2 верно неравенство
Пример 8. Рассмотрим множество Х произвольной природы. Зададим на нем метрику Вывод: любое множество можно метризовать, т.е. определить расстояние между его элементами. Линейные пространства Понятие линейного пространства играет важную роль в современной математике. Оно является естетсвенным обобщением трехмерного евклидового пространства. В линейном пространстве определены две алгебраические оператии: сложение элементов пространства и умножение их на сколяр (число), удовлетворяющие определённым условиям. Определение 1.Пусть К – поле действительных или комплексных чесел. Непустое множество А называется линейным (векторным) пространством над полем К,если для любых двух его элементов х и в определена их сума х+уÎА и для любого числа lÎK определено произведение l×х ÎА так, что эти оператии удовлетворяют следующим аксиомам: 1) x + y = y + x, " x,yÎ А; 2) (x + y) + z = x + (y + z), "x,y,z Î А; 3) $ qÎ А такой, что x + q= x, "xÎ А; 4) " xÎ А $ - xÎ А такой, что x + (- x) = q; 5) 1× x = x "xÎ А; 6) l(x + y) = lx + ly, "x,уÎ А, "lÎ К. 7) (l + m) х = lх + mх, "xÎ А и"l,m Î К. 8)(lm) x = l(mx), "xÎ А и"l,mÎ К. Элементы этого пространства называют векторами. Элемент q– нулевым элементом, (-х) – элементом противоположным элементу х, элемент x - y = x + (- y) – разностью элементов x и y. Линейное пространство над полем R называется действительным линейным пространством, а линейное пространство над полем С комплексных чисел – комплексным линейным пространством. Свойства линейных пространств подробно изучаются в курсе линейной алгебры. Рассмотрим только некоторые примеры линейных пространств, которые используются в курсе математического анализа. Примеры линейных пространств Пример 1.Множество действительных чесел R с определёнными на нём оператиями сложения и умножения – линейное пространство. Будем обозначать его R или R1 . Пример 2. Рассмотрим множество Rnразнообразных упорядоченных n –ок действительных чесел. Определим на Rnоператии сложения и умножения на число: x + y = ( x1 + y1 , x2 + y2 ,…, xm + ym ); lx = (lx1 , lx2 ,…,lxm), где x = (x1 , x2,…, xm), (y1, y2,…, ym), x и y ÎRn, lÎR. Эти оператии удовлетворяют аксиомам (1-8) определения 1, где нулевой элемент q = (0, 0, ..., 0), а элемент противоположный элементу х это элемент - x = (-x1 , -x2,…, - xm). Таким образом, пространство Rn–линейное пространство над полем R. Пример 3. Множество C[a,b] действительных функций, определенных и непрерывных на отрезке [a,b] – линейное пространство над полем R. Определим операции сложения функций: (x + y)(t) = x(t) + y(t) Î C[a,b] иумножения их на действительное число: (lx)(t) = lx(t) Î C[a,b]. Во всех примерах оператии над элементами множеств сводятся к оператиям над числами, поэтому верность аксиом 1-8 очевидна.
Поиск по сайту: |
 . Напомним, что расстояние между двумя точками М1(х1,y1) и М2(х2,y2) плоскости вычисляется по формуле формуле
. Напомним, что расстояние между двумя точками М1(х1,y1) и М2(х2,y2) плоскости вычисляется по формуле формуле
 . В частности
. В частности = X2.
= X2. .
. r (x,y)
r (x,y)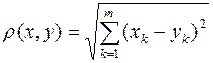 "x,yÎRm.(2)
"x,yÎRm.(2) (3)
(3)

 4
4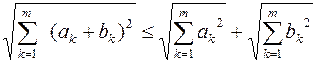 . (4)
. (4)

 .4
.4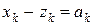 ,
, 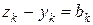 Þ
Þ  .(5)
.(5) Þ
Þ , (6)
, (6) Þ
Þ (7)
(7)
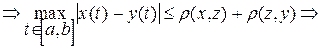 Þr(x,y) £ r(x,z) + r(z,y). 4
Þr(x,y) £ r(x,z) + r(z,y). 4 . Для любых двух последовательностей х = х1, х2, ... и в = у1, у2 ... из множества l2 обозначим
. Для любых двух последовательностей х = х1, х2, ... и в = у1, у2 ... из множества l2 обозначим . (9)
. (9) сходится, то формула (9) задает функтию для любых х, уÎl2. Сходимость ряда легко доказатьь с помощью признака сравнения, если учесть, что ряды
сходится, то формула (9) задает функтию для любых х, уÎl2. Сходимость ряда легко доказатьь с помощью признака сравнения, если учесть, что ряды  сходятся, и верно неравенство
сходятся, и верно неравенство  .
. Þ r(x,y) £ r(x,z) + r(z,y). 4
Þ r(x,y) £ r(x,z) + r(z,y). 4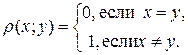 Пара (Х;ρ) – метрическое пространство.
Пара (Х;ρ) – метрическое пространство.