 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Непрерывные отображения компактных пространств
1o. Понятия компактного пространства и компактного множества. Необходимое условие компактности множеств Определение 1. Метрическое пространство X = (X, r) называется компактным (компактом), если из любой последовательности (xn)точек этого пространства можно выделить подпоследовательность Определение 2. Множество Е Ì Х называется компактнымв м.пр. Х, если из любой последовательности точек множества Е можно выделить подпоследовательность, сходящуюся по метрике r к элементу множества Е или другими словами: если подпространство (Е, r) - метрической пространства (X, r)является компактом. Пример 1.Пространство Rне является компактом, т.к. существует последовательность (n), nÎN,из которой нельзя выделить подпоследовательность, сходящуюся в R. Пример 2. Любое конечное множество Е точек метрического пространства (X, r) – компактное множество в этом пространстве. Пример 3. Пусть подпоследовательность ( Теорема 1.Если множество Е замкнутое в компактном метрическом пространстве (X,r), то оно компактное в этом пространстве. ◄ Рассмотрим
Отсюда следует, что в любой ε–окрестности точки а есть члены подпоследовательности Теорема 2(I необходимое условие компактности). Если множество Е Ì Х компактное в м.пр. (X, r), то оно замкнутое в этом пространстве.
Пример 4. Интервал (a,b) не может быть компактным множеством в пространстве R, т.к. не является замкнутым множеством. Теорема 3(II необходимое условие компактности). Если множество Е Ì Х компактное в м.пр. (X, r), то оно ограниченное в этом пространстве.
Таким образом построили последовательность (xn), члены которой удовлетворяют неравенству (1). По условию Е компактное Þ существует подпоследовательность (2) но для этих же номеров kп (т.к.
По аксиоме метрики Получили противоречие. 4 Замечание 1.Теоремы обратные теоремам 2 и 3 вообще говоря не имеют места. Теорема 4 (критерий компактности в Rm). Для того, чтобы множество ЕÌ Rm было компактным в м.пр. Rm, необходимо и достаточно, чтобы оно было замкнутым и ограниченным в Rm. Доказатьельство необходимости следует з теорем 2 и 3. 3Достаточность. Рассмотрим произвольную последовательность (xn)из Е. Т.к. множество Е ограниченное в м.пр. Rm (по условию теоремы), то и последовательность (xn) – ограниченная. Поэтому по теореме Больцана-Вейерштрасса из неё можно выделить подпоследовательность Пример 5. Множества Е= ÌR – компактное множество. Пример 6. в пространстве Rm–компактное множество. Пример 7.Множество ÌR не будет компактным множеством, т.к. не является замкнутым. 2o. Непрерывные отображения компактных множеств и их свойства Теорема 5.Пусть f – непрерывное отображение метрического пространства Х в метрыческое пространство Y (f: Х ◄ Рассмотрим произвольную последовательность Пример 8. Пусть задано отображение f: R f(x) = x2; D( f ) =[1,2]ÌR – компактное множество в метрическом пространстве R; E( f ) = [1,4]Ì R – компактное множество в пространства R. Теорема 6.Если отображение f: Х Замечание 2. Теорема 6 – обобщение теоремы Кантора для действительной функции одной действительной переменной. Определение 3.Пусть задано множество ЕÌХ.Отображение f: Х Теорема 7(I теорема Вейерштрасса). Если отображение f компактного метрического пространства Х в метрическое пространство Y непрерывное, то оно ограниченное.
Вспомним свойства верхней (нижней) грани числового множества. Верхняя (нижняя) грань a множества ЕÌR удовлетворяет следующим условиям: 1) "хÎЕ Þ х£a (х³a); 2) "e>0 $хÎ Е, что х >a-e (x<a+e). Лемма. Замкнутое ограниченное сверху (снизу) числовое множество EÌR содержит свою верхнюю (нижнюю) грань. Определение 5. Пусть f – отображение метрического пространства Х в метрическое пространство R. Говорят, что f принимает наибольшее (наименьшее) значение в точке хоÎХ , если для любога хÎХ выполняется неравенство Теорема 8(II теорема Вейерштрасса для компактных множеств). Если отображение f компактного метрического пространства Х в метрическое пространство R непрерывное, то оно принимает свои наибольшее и наименьшее значении.
Аналогично даказывается, что отображение f принимает наименьшее значение. Определение 6. Отображение f метрического пространства Х в метрическое пространство Y называется взаимно однозначным, если: 1) любому элементу х ÎХ соответствует единственный элемнт уÎ Y и 2) любой элементу уÎ Y соответствует единственному элемнту х ÎХ. Теорема9. Пусть f – взаимно однозначное отображение метрического пространства Х в метрическое пространство Y. Если f – непрерывное отображение, то и обратное ему отображение f -1 также непрерывное. Доказательство сам-но [1 ,ст.33].
Поиск по сайту: |
 , сходящуюся по метрике r к элементу пространства Х.
, сходящуюся по метрике r к элементу пространства Х. члены которой принадлежат ЕÌХ. Т.к. м.пр. (X,r) – компактноя, то для этой последовательности существует подпоследовательность
члены которой принадлежат ЕÌХ. Т.к. м.пр. (X,r) – компактноя, то для этой последовательности существует подпоследовательность  .
. ) выполняется (1), т.е.
) выполняется (1), т.е. (3)
(3)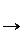 Y). Если множество ЕÌХ – компактное множество в м.пр. Х, то егo образ f(E) – компактное множество в м.пр. Y.
Y). Если множество ЕÌХ – компактное множество в м.пр. Х, то егo образ f(E) – компактное множество в м.пр. Y.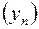 , члены которой принадлежат образу Е, множеству f(E) Ì U . Пусть
, члены которой принадлежат образу Е, множеству f(E) Ì U . Пусть  какой-нибудь прообраз
какой-нибудь прообраз  , т.е.
, т.е.  и
и  . Эта точка является предельной точкой для последовательности
. Эта точка является предельной точкой для последовательности  , члены которой являются образами соответствующих членов последовательности
, члены которой являются образами соответствующих членов последовательности  ). По условию теоремы f – непрерывное отображение метрической пространства Х в метрическое пространство Y Þ (по определению непрерывного отображения) для последовательности
). По условию теоремы f – непрерывное отображение метрической пространства Х в метрическое пространство Y Þ (по определению непрерывного отображения) для последовательности 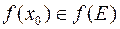 Þ f(E) – компактное множество. ►
Þ f(E) – компактное множество. ►