 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Производительность RFCS-схемы
Для RFCS-схемы вероятности возникновения одной из четырех возможных ситуаций, среднее время выполнения задачи
В приведенных уравнениях используются следующие обозначения:
Оценка плюс — двухмодульных отказоустойчивых вычислительных систем. Для аналитической модели, разработанной здесь, принимается, что сбои, возникающие в каждом из двух модулей, независимы друг от друга. Принято, что возникновение сбоя в модуле происходит согласно процессу Пуассона с интенсивностью λ. Принято, что процессорные модули подвержены сбоям в течение всей операции, включая интервалы контрольных точек и восстановления.
Когда остается выполнить только один интервал после того как обнаружен сбой вследствие сравнения с контрольной точкой (как в ситуациях 2-6), параллельное восстановления для завершения задачи невозможно. Следовательно, наш анализ принимает, что параллельное восстановление возможно только, когда число невыполненных интервалов контрольной точки, по крайней мере, два. Если количество невыполненных интервалов - 0 или 1, то пара ВМ выполняет откат назад к предыдущей контрольной точке (никакое параллельное восстановления не предпринимается).
Предположим, что вероятность возникновения ситуации от (1) до (6) представлена значениями от P1 до P6, соответственно, рассмотренными в Разделе 3.1. Из обсуждения в разделе 3.1 получены следующие выражения:
Время реализации каждой ситуации равно, соответственно:
Пусть τk - время, требуемое, чтобы выполнить последние k интервалов решения задачи. τn - время, требуемое, чтобы завершить задачу. После того как задача выполнила первый интервал, время, требуемое, чтобы завершить остающуюся задачу будет -
Теперь, мы получаем рекурсию для
Если сбой происходит в любом другом интервале, исключая последние два, то выполняется параллельное восстановление. Следовательно, для k = 3, имеем следующую рекурсию: для получения среднего времени выполнения задачи после k интервалов, считая в обратном порядке - с последнего:
Поиск по сайту: |
и дисперсия 
приведены в [51]:
,
,
,
.
,
,
,
,
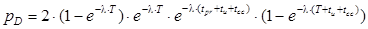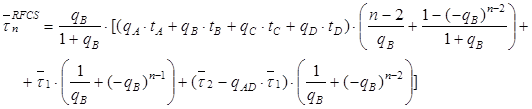
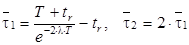и 
.
, 
, 
, 
, 
, 
.
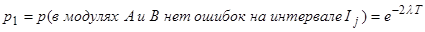
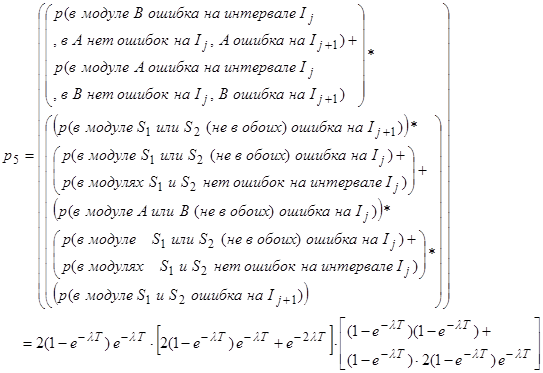
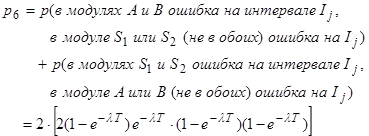
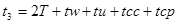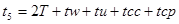. Для другого k ≥ 1, 
определено аналогично. Также, τ0 = 0.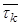
- Ожидаемое (среднее) значение 
. Напомним, что если сбои происходят в последних двух интервалах, система совершает откат назад. Следовательно,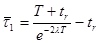
, 
,