 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение усилий по линиям влияния от подвижной системы связных грузов ⇐ ПредыдущаяСтр 6 из 6
Пусть требуется определить максимальную и минимальную величину Zк по л.в. Zк от одиночного подвижного груза Р = 20 кН. Для этого достаточно совместить груз с максимальной и минимальной ординатами л.в. Zк. В рассматриваемом примере (рис. 11г): MA max = P ∙ymax = 20 · 3,2 = 64 кНм; MA min = P ∙ymin = 20 · 4 = 80 кНм. При этом выясняется невыгодное положение подвижной силы: точки Г и Б соответственно. Несколько сложнее определить максимальное (минимальное) значение от подвижной системы связных грузов(железнодорожный поезд, колонна автомашин, трамвай и т.п.). Заданием предусматривается определение наибольшей величины одной реакции Vк, линия влияния которой имеет треугольное очертание внешнего вида, от автопоезда (рис. 14а). Сначала учитывается движение автопоезда справа налево и выявляется положение критического груза Ркр, который затем располагается над максимальной ординатой линии влияния, что соответствует ее невыгодному загружению. Критический груз легко установить графически (рис. 14б). Для этого вниз от левого конца л.в. VВ последовательно (в порядке расположения грузов поезда (рис. 12а)) откладываем вектора Р1, Р2 …. Последний из них соединяем с правым концом линии влияния (луч 2). Луч 3, построенный из точки положения ymax параллельно лучу 2, укажет, какой груз критический. В нашем случае Ркр = Р3 = 30 кН. Проверим это по критериям: (Rл + Ркр) / a ≥ Rп / b и Rл / а ≤ (Rп + Ркр) / b. В нашем случае: Ркр = Р3 = 30 кН; Rл = Р1 + Р2 = 50 Кн – равнодействующая левых сил; Rп = Р4 + Р5 = 40 кН – равнодействующая правых сил. Тогда получим: (50+30) / 9 = 8,89 > 40 / 6 = 6,67 и 50 / 9 = 5,56 < (40+30) / 6 = 11,67 Критерии удовлетворяются, следовательно, критический груз найден правильно. Располагаем критический груз над максимальной ординатой линии влияния (рис. 12б) и вычисляем
Рис. 14
Затем аналогичным путем учитывается движение поезда слева направо (построения даны на рис. 14б пунктиром)
Сравнение этих значений позволяет установить наибольшее VВmax= 152 кН.
ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ 1. Что такое поэтажная схема многопролетной статически определимой балки? Как она строится? 2. Каков порядок расчета многопролетной статически определимой балки на неподвижную нагрузку? 3. Как вычисляются перемещения в многопролетной статически определимой балке от смещения опор? 4. Как вычисляются перемещения в многопролетной статически определимой балке от изменения температурного режима? 5. Что называется линией влияния? Какие методы применяют для построения линий влияния? 6. В чем отличие линии влияния от эпюры? 7. Построение л.в. опорных реакций и внутренних усилий в балке на двух опорах. 8. Построение л.в. опорных реакций и внутренних усилий в консольной балке. 9. Какой алгоритм построения л.в. многопролетной статически определимой балки? 10. Как вычисляются усилия по л.в. от действия внешней нагрузки? 11. Как определить невыгодное положения нагрузки на сооружение?
ЛИТЕРАТУРА
Основная
1. Дарков А.В. Строительная механика: учебник / А.В. Дарков, Н.Н. Шапошников. М.;Краснодар: Лань, 2008. - 656 с. 2. Строительная механика: Кн. 1: Статика упругих систем: учебник / В. Д. Потапов [и др.]. - М.:Высшая школа, 2007. - 511 с. 3. Киселев В.А. Строительная механика. Общий курс: учебник / В.А. Киселев. М.: Стройиздат, 1986. 520 с. 4. Строительная механика / Ю.И. Бутенко, Н.А. Засядько, С.Н. Кан и др. К.: Выща школа, 1989. 479 с. 5. Селюков В.Н. Расчетно-проектировочные работы по строительной механике / В.Н. Селюков. Минск: Вышэйшая школа, 1989. 205 с. 6. Расчет статически определимых плоских стержневых систем на неподвижные и подвижные нагрузки. Определение внутренних усилий: методические указания / сост.: П.К. Семенов, Е.А. Петрунина, Саратов: СГТУ, 2006. 32 с.
Дополнительная
7. Абовский Н.П. Современные аспекты активного обучения. Строительная механика. Теория упругости. Управление строительными конструкциями / Н.П. Абовский, Л.В. Енджиевский, В.И. Савченков и др. Красноярск: КрасГАСА, 2007. 472 с. 8. Абовский Н.П. Регулирование. Синтез. Оптимизация / Н.П. Абовский, Л.В. Енджиевский, В.И. Савченков и др. М.: Стройиздат,1993. 456 с. 9. Абовский Н.П. Избранные задачи по строительной механике и теории упругости / Н.П. Абовский, Л.В. Енджиевский, В.И. Савченков и др. М.: Стройиздат,1978. 192с. 10. Расчет статически определимых систем на неподвижные нагрузки по программе INTAB –12 для ПЭВМ: методические указания / сост.: И.В. Кривошеин, Е.А. Петрунина. Саратов: СГТУ, 2000. 29с.
ПРИЛОЖЕНИЕ 1
Поиск по сайту: |
 по общим правилам (рис. 13):
по общим правилам (рис. 13):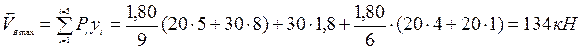

 = 1,80 / 9 · (20 ·2 + 20 · 6 + 30 · 8) + 30 · 1,8 + 1,80 / 6 · 20 ·3 = 152 кН.
= 1,80 / 9 · (20 ·2 + 20 · 6 + 30 · 8) + 30 · 1,8 + 1,80 / 6 · 20 ·3 = 152 кН.