 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
От изменения температурного режима
Пусть температурный режим эксплуатации балки изменился и стабилизировался. Верхние волокна по всей длине балки нагрелись на tв = 500 С, нижние – на tн = 100 С (рис. 10а). Распределение температур по высоте поперечного сечения сохраняется линейным. Материал балок ВСт3г не меняется по длине. Коэффициент линейного расширения α = 0,12·10-4 0С-1 сохраняется постоянным. Высоту поперечных сечений балки примем по результатам расчета на прочность: участок А – В hАВ = 0,22 м ,двутавр №22; участок Б – Д hБД = 0,18 м, двутавр №18, участок Д – З hДЗ = 0,24 м, двутавр №24. Для принятых симметричных сечений температура волокна на нейтральной оси tc = (tB + tH) / 2 = (50 + 10) / 2 = 300 C, разность температур в крайних волокнах ∆t = 400 С. Для определения перемещений выбирается (обычным путем) единичное вспомогательное состояние и для него строятся эпюры M и N. Позднее для каждого участка вычисляются площади FM и FN эпюр M и N соответственно. Искомое перемещение вычисляется по формуле:
∆t = Σα ∙ tc ∙FN + Σα ∙∆t / h · FM.
Здесь первый член учитывает влияние равномерного нагрева и ему присваивается знак плюс при качественно одинаковом изменении длины волокна нейтральной оси в температурном и единичном состояниях и минус – в противном случае. При вычислении вертикальных перемещений в горизонтально расположенных балках, не имеющих наклонных опорных связей, этот член отсутствует, т.к. N = 0. Второй член учитывает влияние неравномерного нагрева и ему присваивается знак плюс при качественно одинаковом изменении кривизны участка от действия температур и в единичном состоянии и знак минус – в противном случае. Сопоставление кривизны участков удобно проводить по специальным значкам ( Для примера вычислим прогиб ft в середине наибольшего пролета балки от изменения температурного режима (рис. 10а).
∆t = ft = Σα ∙∆t / h ·FM
Полный прогиб балки в середине наибольшего пролета равен:
f = fP + fK + fC = 6,57 + 29,1 + 1,68 = 37,35 см.
Рис. 10
РАСЧЕТ НА ПОДВИЖНЫЕ НАГРУЗКИ
Общий порядок расчета Сложность расчета балок на подвижные нагрузки обусловлена изменением их положения и качественным изменением вида подвижных нагрузок. Эта задача успешно преодолевается предварительным построением специальных графиков от простейшей подвижной нагрузки Линией влияния некоторого фактора Zк (например, опорной реакции в к-ой опорной связи или внутренних усилий Mк, Qк в к-ом сечении) называют график изменения Zк в к-ом сечении или опорной связи при перемещении по балке подвижной силы Р = 1. Методика построения линий влияния для простых балок с необходимыми уравнениями приводится в учебниках [1-6]. Основные результаты даются в приложении 2 для двух типовых задач: первая – простая двухопорная балка, вторая – консольные балки. В многопролетных балках линии влияния строятся в соответствии с «поэтажной» схемой (без учета внешних подвижных нагрузок) в следующем порядке: 1. Для элемента, которому принадлежит данная опора или сечение, линии влияния строятся по приложению 2. При этом, если к-ое поперечное сечение расположено между опор, поддерживающих данную балку, используется первая типовая задача; если за пределами – вторая. 2. Для балок, расположенных на нижних ярусах «поэтажной» схемы обсуждаемые линии влияния будут принимать нулевые значения, т.к. сила 3. Для балок верхних ярусов линии влияния строятся путем последовательного соединения ординат линии влияния балок нижнего яруса, в месте прикрепления к ней «висячей» опоры (поддерживающее балку верхнего яруса) с нулевой ординатой наземной опоры рассматриваемой балки верхнего яруса. При этом все характерные ординаты легко вычисляются из геометрических соображений (по подобию треугольников).
Поиск по сайту: |
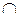 или
или  ), наглядно указывающим характер изменения кривизны (рис. 10а, б).
), наглядно указывающим характер изменения кривизны (рис. 10а, б).
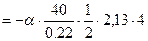
 +
+ 1,398 · 103 · 0,12 · 10-4 = 0,0168 м = 1,68 см.
1,398 · 103 · 0,12 · 10-4 = 0,0168 м = 1,68 см.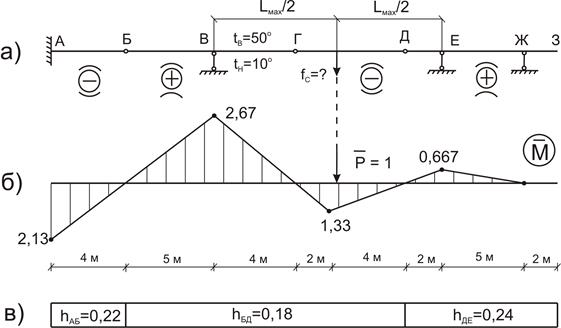
 = 1, называемых линиями влияния. По этим графикам легко вычисляются соответствующие усилия от любых подвижных нагрузок.
= 1, называемых линиями влияния. По этим графикам легко вычисляются соответствующие усилия от любых подвижных нагрузок.