 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Вычисление прогиба и расчет на жесткость
Расчет на неподвижные нагрузки завершается вычислением прогиба в середине наибольшего пролета заданной балки по формуле Мора:
где (рис. 3г);
Сначала определяем пролеты заданной балки, то есть расстояния между соседними наземными опорами. В нашем примере (рис. 3а) они будут равны lAB = 9м, lBE = 12м, lЕЖ = 5м. Отсюда следует, что середина наибольшего пролета находится на расстоянии 6м от опоры В в сторону опоры Е. Приложив в этом сечении
Рис. 7
Используя описанный прием, следует учитывать особенности конкретной «поэтажной» схемы и положения единичной силы. Так, если бы сила После построения эпюры М и определения относительных изгибных жесткостей участков (рис. 7в): EJАБ = 1,36 EJ0; EJБА = EJ0, EJАЗ = 1,88 EJ0 (изгибные жесткости выражены через EJ0 = 3864 кНм2), вычисляется искомый прогиб. При этом на простых линейных участках эпюр удобно использовать прием А.Н. Верещагина. На сложных параболических – формулу Симпсона (ниже такие члены выделены одной чертой), при «перемножении» трапеции – формулу трапеций (выделено двумя чертами).
Рис.8
Отсюда относительный прогиб равен f/l = 6,57 см /1200 см = 1/183, что по условиям эксплуатации сооружений является недопустимым. Предельные относительные прогибы составляют для рассматриваемых балок 1/500 ÷ 1/700. Поэтому из условия жесткости в целях исключения чрезмерных деформаций необходимо развить поперечное сечение до EJ0треб = 253,85 · 700 / 12 = 14808 кНм2, т.е. J0треб = 7051 см4 . Или по участкам (рис. 7в) JАБтр = 9589 см4, JБДтр = 7051 см4, JДЗтр = 13256 см4. На участке А – Б принимаем двутавр №36 (JАБ = 13380 см4 ), на участке Б – Д двутавр №30 (JБД = 7080 см4 ), на Д – З №40 (JДЗ = 19062 см4 ). Следует подчеркнуть, что условия жесткости сооружений, особенно транспортных, вызывают дополнительные затраты материалов. Так, в нашем примере увеличение начальных поперечных сечений балок Fjn до последних Fjж на каждом участке длиной ij приводит к возрастанию материалоемкости конструкции на ∆G процентов:
+ (72,6 – 34,8) · 900) ·100 / (30,6 ·400 + 23,4 · 1500 + 34,8 · 900) = 103,2 %. Этот пример подчеркивает необходимость поиска более рациональных решений расчетно-проектировочной задачи. В частности, путем подбора рационального распределения жесткостей EJj по участкам; целенаправленного изменения структуры расчетной схемы; введения дополнительных связей и т.д.
Поиск по сайту: |

 – расчетная эпюра изгибающих моментов от заданных нагрузок
– расчетная эпюра изгибающих моментов от заданных нагрузок – эпюра изгибающих моментов единичного состояния, построенная от силы
– эпюра изгибающих моментов единичного состояния, построенная от силы  = 1, приложенной в середине наибольшего пролета;
= 1, приложенной в середине наибольшего пролета;
 Порядок построения эпюры
Порядок построения эпюры  и
и  . Здесь линейные эпюры претерпевают излом и проходят через следующие нулевые точки Б и Ж. На консоли Ж – З внутренние усилия отсутствуют, т.к. консоль в единичном состоянии не загружена.
. Здесь линейные эпюры претерпевают излом и проходят через следующие нулевые точки Б и Ж. На консоли Ж – З внутренние усилия отсутствуют, т.к. консоль в единичном состоянии не загружена.

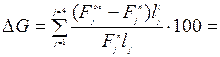 ((61,9 – 30,6) · 400 + (46,5– 23,4) ·1500 +
((61,9 – 30,6) · 400 + (46,5– 23,4) ·1500 +