 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Коррелированные выборки ⇐ ПредыдущаяСтр 6 из 6
В педагогических исследованиях, довольно часто, необходимо определить достоверность различий между средними показателями одной и той же группы испытуемых, полученных в различное время (например, до и после педагогического эксперимента). Применять критерий Стьюдента, использовав его формульное выражение (7) для случая независимых выборок, нельзя, так как в обеих выборках участвуют одни и те же испытуемые и результаты исследований по окончании эксперимента сильно зависят от результатов исходных данных исследований. Такие выборки называют коррелированными. Критерий Стьюдента в случае коррелированных выборок вычисляется по формуле
где r – коэффициент корреляции между сравниваемыми группами по изучаемому признаку. Для того чтобы не вычислять коэффициента корреляции и упростить вычисления можно использовать методику вычислений, предложенную в работе [1], основанную на определении разности между значениями признаков для каждой пары. По существу речь идет об определении статистически значимой достоверности в приросте результатов, определяемых как разность значений признака для каждой варианты (и в целом для всей выборки испытуемых) до и после педагогического эксперимента. Рассмотрим последовательность выполнения необходимых операций на следующем примере. Предварительно введем обозначения для статистических параметров распределения:
На группе из 16 студентов (N=16) была проверена эффективность новой методики развития силы и силовой выносливости с применением специальной аппаратуры (вибротренажёр). О результатах эксперимента судили по числу подтягиваний в висе на перекладине до начала и после окончания тренировочного периода (табл. 13). Средняя разность (
Таблица 13.
В первой колонке таблицы 13 приведены порядковые номера испытуемых и их общее число (N=16). Во второй и третьей колонках приведены результаты в подтягивании у испытуемых до эксперимента (колонка 2) и после эксперимента (колонка 3). Результаты вычислений разности по каждой варианте до и после эксперимента, их суммы и средней арифметической разности (прироста) приведены в колонке 4. В колонке 5 приведены отклонения каждой варианты (di) от средней разностью ( И в колонке 6 дана сумма квадратов отклонений от средней разности. Средний квадрат отклонений будет равен
Среднее квадратическое отклонение соответственно равно
Определяем среднюю ошибку разности
Отсюда следует, что
По таблице 1 Приложений критическое значение t для уровня значимости 0,05 при f=N-1=15, будет равняться 2,13, а t01=2,95. Поэтому с вероятностью более чем в 95% можно утверждать, что изменения в количестве подтягиваний на перекладине являются неслучайными.
Литература
1. Годик М.А. Спортивная метрология: Учебник для институтов физической культуры. – М.: Физкультура и спорт, 1988. 2. Демьяненко Ю.К. Основные приемы математической обработки и интерперетации результатов исследований по физической подготовке и спорту. – Л., 1971. 3. Лакин Т.Ф. Биометрия. – М.: Высшая школа, 1968. 4. Плохинский Н.А. Биометрия. – М., МГУ, 1970. 5. Урбах В.Ю. Биометрические методы. – М.: Наука, 1964.
П Р И Л О Ж Е Н И Е
Таблица 1.
Граничные значения t (критерий Стьюдента).
Поиск по сайту: |
 (9)
(9) - результат i-го испытуемого до начала эксперимента;
- результат i-го испытуемого до начала эксперимента; - результат i-го испытуемого после эксперимента;
- результат i-го испытуемого после эксперимента; - разность результатов у i-го испытуемого, определяемая по значениям, показанным после и до проведения эксперимента;
- разность результатов у i-го испытуемого, определяемая по значениям, показанным после и до проведения эксперимента;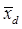 - средняя арифметическая разности (прироста) результатов педагогического эксперимента.
- средняя арифметическая разности (прироста) результатов педагогического эксперимента. ) в нашем примере вычисляется следующим образом:
) в нашем примере вычисляется следующим образом: =
=  (10)
(10)



 . (11)
. (11) (12)
(12) (13)
(13) (14)
(14)