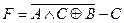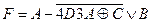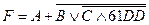|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Формы представления чисел.
В цифровых устройствах используются две формы представления чисел: с фиксированной и плавающей точкой. Числа с фиксированной точкой. В ячейке для хранения числа с фиксированной точкой один разряд используется в качестве знакового, в нем записывается в закодированной форме знак числа: 0 — в случае положительного, 1 — в случае отрицательного числа. Остальные разряды используются для хранения абсолютного значения числа. Точка, отделяющая целую часть числа от ее дробной части, занимает фиксированное положение: часто перед старшим разрядом либо после младшего разряда. В первом случае для всех представляемых в этой форме чисел абсолютное значение меньше единицы. Например, число —0,1011012 следующим образом разместится в элементах запоминающей ячейки:
Свободные младшие разряды заполняются нулями. Так как в этом случае предусматривается хранение лишь дробной части числа, то не только исходные данные, но и результаты всех проведенных над ними операций должны быть числами, абсолютное значение которых меньше единицы. Выполнение этого условия обеспечивается выбором определенных масштабных коэффициентов, на которые умножаются исходные данные задачи. Неправильный выбор коэффициентов может вызвать так называемое переполнение разрядной сетки — возникновение ошибки, если в результате выполнения операций в числе образуется целая часть, для хранения которой в разрядной сетке не предусмотрено места, и она теряется. Необходимость в масштабировании данных составляет один из недостатков представления чисел с фиксированной точкой; другой недостаток этой формы — низкая точность представления чисел, абсолютное значение которых мало (нули в старших разрядах приводят к уменьшению числа разрядов, занимаемых значащей частью числа, и к снижению точности Представ лен и я числа). Во втором случае, когда точка фиксируется после младшего разряда, числа с фиксированной точкой — целые. Например, число 110112 будет размещено в ячейке памяти следующим образом:
Здесь свободные старшие разряды заполняются нулями. Если n - число разрядов ячейки, то диапазон модулей представимых в ней целых чисел: 0 ... (2n-1 — 1). Числа с плавающей точкой. Форма с плавающей точкой предусматривает представление числа в показательной форме. Например, десятичное число 685, 7310 представляется в форме 0,68573·103; здесь 0,68573 — мантисса, 10 — основание десятичной системы счисления, 3 — порядок. Двоичное число 0,0001011012 представляется в виде 0,101101·10-11; здесь 0,1011012 — мантисса, 102 —основание двоичной системы счисления,—112 — порядок. В ячейке памяти такие числа хранятся в виде двух групп цифр: первая группа, называемая мантиссой, определяет само число, вторая группа, называемая порядком,— место точки в числе. Приведенное выше двоичное число может иметь следующее размещение в элементах запоминающей ячейки:
Соответствующим выбором значения порядка можно добиться, чтобы старший разряд мантиссы не был равен нулю. При этом образуется так называемая нормальная форма. Определим диапазон двоичных чисел, которые могут быть представлены в ячейке памяти в нормальной форме. Обозначим k — число разрядов, отведенных в ячейке для хранения абсолютного значения порядка. Положительное число в ячейке будет иметь наименьшее значение, если минимальное значение будет иметь мантисса (все ее разряды, кроме старшего, будут содержать нуль: Nmin = 2-(2k — 1) /2 = 2-2k Максимальное число в ячейке образуется при максимальном значении мантиссы (когда мантисса содержит во всех разрядах единицу: 0,11 ...12 ≈ 1) и положительном порядке, имеющем максимальное значение (т. е. если все разряды порядка содержат единицу: 11 ...12= 2k — 1). Следовательно, максимальное значение числа Nmax = 2(2k — 1) Итак, диапазон представимых чисел в нормальной форме равен Nmin… Nmax = 2-2k … 2(2k — 1) Как видим, этот диапазон определяется лишь k. Если диапазон представимых чисел, как показано выше, определяется числом разрядов, отведенных в ячейке памяти для хранения порядка, то точность представления чисел определяется числом разрядов, выделенных для хранения мантиссы. Нормальная форма позволяет получать представление чисел в широком диапазоне с одинаковой относительной погрешностью. Использование формы с плавающей точкой позволяет часто обходиться без масштабирования данных. В тех же случаях, когда оно требуется, выбор масштабных коэффициентов не представляет трудностей. Однако выполнение операций над числами с плавающей точкой сложнее, чем над числами с фиксированной точкой. Операции над числами. Операции, проводимые над числами, делятся на две независимые группы: арифметические и логические. Арифметические операции. Арифметические операции – операции, проводимые непосредственно над всем числом. Простейшие арифметические операции (сложение и вычитание) производятся во всех системах счисления по одинаковым законам. Организация операции сложения:
Где: Аn – n-ый разряд первого слагаемого; Bn – n-ый разряд второго слагаемого; F’n – результат операции между соответствующими разрядами; Fn – записываемое значение результата в n-ом разряде; R – основание системы счисления, в которой производится операция. Организация операции вычитания: Вычитание может быть организованно двумя способами: вычитание непосредственно по законам алгебры и с использованием алгебраического сложения с числами, представленными в дополнительном коде. Первый тип представлен следующими выражениями.
Второй тип - алгебраическое сложение с использованием дополнительного кода, является наиболее приемлемым в микропроцессорной технике и его сущность поясняется в ниже приведенном примере. Пусть требуется сложить два десятичных числа N1 = 831 и N2 = -376. Введем дополнительное понятие положительного числа как «0» и отрицательного числа как «1». Так как второе слагаемое — отрицательное число, пользование приемом, представленным ранее, потребовало бы последовательности действий с заемами из старших разрядов. Предусматривать в цифровом устройстве дополнительно такую последовательность действий является затруднительным. Искомый результат может быть получен и с использованием последовательности действий с передачей переносов в старшие разряды, которые используются при сложении положительных чисел. Предварительно введем дополнительное понятие положительного числа как «0» и отрицательного числа как «1». В результате этого N1 = 0 831 и N2 = 1 376. Далее отрицательное число 1 376 преобразовываем в дополнительный код по следующему закону: во всех разрядах, запишем дополнение до 9 к цифрам этих разрядов (до R-1 в случае использования других систем счисления) и затем прибавим единицу в младший разряд. Число N2 = 1 376 в дополнительном коде есть N2 доп = 1624. Далее произведем сложение по правилам сложения с передачей переносов в старшие разряды (т. е. так как складываются положительные числа):
Первое слагаемое, N1 0 8 3 1 Второе слагаемое, N2 доп 1 6 2 4 Сумма 0 4 5 5
При сложении складываются и двоичные цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса. Операции умножения и деления являются более сложными процедурами и организуются путем создания определенных алгоритмов. Операция умножения может быть представлена двумя видами: операцией многократного последовательного сложения и операцией умножения «в столбик» с использованием операций сдвига. Первый тип представляет собой процедуру, при которой первый множитель складывается самим с собой n раз, где n – значение второго множителя. Т.е. данная процедура имеет вид:
Данный способ при достаточно больших множителях является ресурсоемким, и может занимать большое время. Второй тип более сложен по построению, однако скорость вычисления, согласно данного алгоритма, выше. Операция умножения чисел, представленных в форме с фиксированной точкой, включает в себя определение знака и абсолютного значения произведения. Определение знака произведения. Знаковый разряд произведения может быть получен суммированием знаковых разрядов сомножителей без формирования переноса (так называемым суммированием по модулю 2). Действительно, при совпадении цифр знаковых разрядов сомножителей (0 ... и 0..., либо 1 ... и 1 ...) их сумма по модулю 2 равна 0, т. е. соответствует знаковому разряду произведения двух сомножителей, имеющих одинаковые знаки; при несовпадении цифр знаковых разрядов эта сумма будет равна 1, что также соответствует знаковому разряду произведения двух сомножителей с разными знаками. Определение абсолютного значения произведения. Абсолютное значение произведения получается путем перемножения чисел без учета их знаков (так называемого кодового умножения). Эта операция имеет следующий вид.
Как видно из примера, в процессе выполнения операции умножения формируются частичные произведения (произведения множимого на цифры разрядов множителя), которые суммируются с соответствующими сдвигами друг относительно друга. В цифровых устройствах процессу суммирования частичных произведений придают последовательный характер: формируется одно из частичных произведений, к нему с соответствующим сдвигом прибавляется следующее частичное произведение, к полученной сумме двух частичных произведений прибавляется с соответствующим сдвигом очередное частичное произведение и т.д., пока не окажутся просуммированными все частичные произведения. Этот процесс суммирования можно начинать с младшего либо старшего частичного произведения. Логические операции. Логические операции – операции, которые выполняются согласно законам булевой алгебры. Данные операции производятся только с числами, представленными в двоичной системе счисления, по разрядно, в соответствии с определенными законами – таблицами истинности. Наиболее распространены следующие логические операции: «И», «ИЛИ», «НЕ» и «ИСКЛЮЧАЮЩЕЕ ИЛИ» («сложение по модулю «2»»).
Определение: В результате выполнения логической операции «И» функция является истиной только в случае истинности всех операндов.
Операция «ИЛИ».
Определение: В результате выполнения логической операции «ИЛИ» функция является истиной в случае истинности хотя бы одного операнда.
Операция «НЕ».
Определение: В результате выполнения логической операции «НЕ» функция является ложью в случае если операнд был истиной и на оборот.
Операция «ИСКЛЮЧАЮЩЕГО ИЛИ».
Определение: В результате выполнения логической операции «ИСКЛЮЧАЮЩЕГОИЛИ» функция является истиной только в случае истинности одного операнда.
Алгоритмы. На этапе проектирования основной частью является алгоритмизация поставленной задачи, т.е. создание графического материала, поясняющего последовательность определенных действий – алгоритма. Алгоритмы решения задач условно разделяются на три типа: · Общий – алгоритм, содержащий наиболее общие части решения задачи. Например для нахождения функции он содержит следующие блоки: начало решения задачи, загрузка операндов, первая операция, вторая операция, … , n-ая операция, вывод результата, завершение задачи. В данном случае не рассматриваются ни количество разрядов операндов, ни условия, которые могут возникнуть в определенном действии (переносы, заемы, сдвиги и т.д.). · Уточненный. В данном случае алгоритм содержит расширенное (уточненное) количество блоков, поясняющее более подробно некоторые блоки общего алгоритма. Так некоторая операция из общего алгоритма (например сложение) будет содержать следующие блоки: взятие младшего разряда первого операнда, взятие младшего разряда второго операнда, операция между ними, запись результата в соответствующий разряд, в случае переполнения, прибавление «1» в следующий разряд, проверка наличия следующих разрядов операндов, участвующих в операции. Далее, в случае наличия следующих разрядов - переход к следующему разряду первого операнда, переход к следующему разряду второго операнда, и повторение операции. В случае отсутствия – завершение данной операции и переход к следующей. · Расширенный (подробный) алгоритм. В этом случае расписываются все действия, которые присутствуют при решении поставленной задачи. Данный тип алгоритмов применяется при решении поставленных задач с использованием вычислительной техники и создается индивидуально для каждой системы. Согласно ГОСТ 19.701-90 (СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ ДАННЫХ И СИСТЕМ. Условные обозначения и правила выполнения) алгоритмы подчиняются следующим положениям. 1. Схемы алгоритмов, программ, данных и систем (далее – схемы) состоят из имеющих заданное значение символов, краткого пояснительного текста и соединяющих линий. 2. Схемы могут использоваться на различных уровнях детализации, причем число уровней зависит от размеров и сложности задачи обработки данных. Уровень детализации должен быть таким, чтобы различные части и взаимосвязь между ними были понятны в целом. 3. В настоящем стандарте определены символы, предназначенные для использования в документации по обработке данных, и приведено руководство по условным обозначениям для применения их в: 1) схемах данных; 2) схемах программ; 3) схемах работы системы; 4) схемах взаимодействия программ; 5) схемах ресурсов системы. 4. В стандарте используются следующие понятия: 1) основной символ-символ, используемый в тех случаях, когда точный тип (вид) процесса или носителя данных неизвестен или отсутствует необходимость в описании фактического носителя данных; 2) специфический символ-символ, используемый в тех случаях, когда известен точный тип (вид) процесса или носителя данных или когда необходимо описать фактический носитель данных; 3) схемо-графическое представление определения, анализа или метода решения задачи, в, котором используются символы для отображения операций, данных, потока, оборудования и т.д. Схема программы (алгоритм выполнения программы) 1. Схемы программ отображают последовательность операций в программе. 2. Схема программы состоит из: 1) символов процесса, указывающих фактические операции обработки данных (включая символы, определяющие путь, которого следует придерживаться с учетом логических условий); 2) линейных символов, указывающих поток управления; 3) специальных символов, используемых для облегчения написания и чтения схемы. Условно-графические обозначения, используемые при построении схем программ приведены в таблице 1.1. Таблица 1.1 УГО используемые при построении схем программ
2. Порядок выполнения работы 2.1. Согласно своему варианту из таблицы 1.2. выбрать число, представленное в десятичной системе счисления и провести перевод его из одной системы счисления в другую: 10 → 2; 10 → 8; 10 → 16. Далее провести проверку, проведя следующие преобразования чисел: 2 → 10; 2 → 16; Таблица 1.2
2.2. Привести число, представленное в различных системах счисления, к нормальному виду. 2.3. Результаты преобразований, согласно п. 1 и 2, занести в таблицу 1.3. ФПЗ - запись числа в форме с плавающей запятой. НФ – нормальная форма записи числа. Таблица 1.3
2.4. Согласно своему варианту из таблицы 1.4. найти значение функции.
Таблица 1.4
2.5. Результаты вычислений в шестнадцатеричной системе счисления представить в таблице 1.5.
Таблица 1.5
2.6. Построить общий и уточненный алгоритмы для нахождения своей функции. 3. Содержание отчета 3.1. Перевод чисел из одной системы счисления в другую. 3.2. Перевод чисел из формы с плавающей запятой в нормальную форму. 3.3. Последовательность вычислений для нахождения результата функции. 3.4. Заполненные таблицы 1.3 и 1.5. 3.5. Общий и уточненный алгоритмы для нахождения своей функции. 4. Контрольные вопросы 4.1. Что подразумевает под собой понятие «система счисления»? 4.2. Принцип перевода чисел из десятичной системы счисления. 4.3. Принцип перевода чисел в десятичную систему счисления. 4.4. Принцип перевода чисел из шестнадцатеричной системы счисления в двоичную и обратно. 4.5. Основное отличие в понятиях «арифметическая операция» и «логическая операция». 4.6. Принцип организации вычитания в вычислительной технике. Что такое дополнительный код? Определение положительного и отрицательного результата. 4.7. Определение и таблицы истинности основных логических операций. 4.8. Состав схемы программ. Основные символы для построения схемы программ.
5. Литература 5.1. Токхейм Р. Основы цифровой электроники /Пер. с англ. под ред. 5.2. Майоров С.А., Кириллов В.В., Приблуда А.А. Введение в микроЭВМ – Л.: Машиностроение, 1988г. – 304с. 5.3. Калабеков Б.А. Микропроцессоры и их применение в системах передачи и обработки сигналов: Учебное пособие для высших учебных заведений. М.: Радио и связь, 1988. – 368с. 5.4. Гилмор Ч. Введение в микропроцессорную технику / Пер. с англ. 5.5. ГОСТ 19.701-90 СХЕМЫ АЛГОРИТМОВ, ПРОГРАММ ДАННЫХ И СИСТЕМ. Условные обозначения и правила выполнения.
Поиск по сайту: |
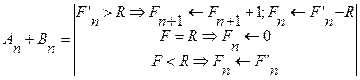 ;
;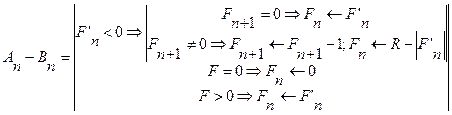 ;
;
 Переносы 1 1
Переносы 1 1 Операция «И».
Операция «И». Обозначение: или .
Обозначение: или .
 Обозначение: или .
Обозначение: или . Обозначение: .
Обозначение: .
 Обозначение: или .
Обозначение: или .