 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Модель Бертрана с дифференцированным продуктом
Стандартная модель Бертрана предполагает совершенную заменимость товаров двух фирм. Однако они могут производить и разнородную (дифференцированную) продукцию. Предположим спрос на товар каждой фирмы описывается уравнением:
где Рj - цена, назначаемая данной фирмой; Рj - цена фирмы-конкурента (i,j = 1,2; i ≠j), причем 0<d<b и а> AC(b-d).Издержки на единицу товара у обеих фирм идентичны, постоянны и равны АС. Товары двух фирм служат несовершенными заменителями друг друга. Прямая ценовая эластичность спроса на товар отрицательна, перекрестная эластичность спроса на товар положительна (что следует из знаков коэффициентов при ценах). Если цена Рi достаточно велика по сравнению с ценой Рj, то объем спроса на товар i-й фирмы равен нулю. Однако при небольшой разнице цен, даже если цена конкурента превышает цену данной фирмы, часть покупателей останется верна данному товару благодаря приверженности марке. Условие d < b означает, что если цены товаров обеих фирм вырастут на бесконечно малую величину ε, объем спроса на оба товара сократится. Условие а > АС(b-d) означает, что если обе фирмы назначат цены на уровне предельных издержек, объемы спроса на их товары будут положительными. Определим результат взаимодействия фирм, то есть найдем такой набор цен (P1*, P2*) что Рi* обеспечивает максимизацию прибыли π = (Рi - АС)Qd(Рi, Pj); i=1,2; j≠i. Вычислим для любого Pj функцию реакции i-й фирмы, максимизирующую (Рi - АС)Qd(Рi, Рj). Пусть Ri(Рj) - функция реакции фирмы на цену конкурента. Для рассматриваемого примера функция реакции будет иметь вид:
Известно, что функции реакции обеих фирм симметричны. Решив систему из двух уравнений - функций реакций фирм, - получим следующий результат:
При такой комбинации цен двух фирм они будут получать положительную прибыль, так как
то есть разница между равновесной ценой и предельными (и средними) издержками положительна для каждой фирмы. Итак, дифференциация продукта смягчает ценовую конкуренцию. В большинстве случаев производители сами выбирают степень дифференциации продукта. Модель Эджворта Модель Эджворта является еще одной версией модели Бертрана, которая определяет ценовую конкуренцию фирмы с ограниченными размерами выпуска. Рассмотрим, установление равновесия на рынке при ценовом взаимодействии двух фирм ограниченности их совокупных мощностей. Предположим, что выпуск каждой фирмы, действующей в отрасли, ограничен величиной К, составляющей половину того объема выпуска отрасли, на который предъявляется спрос при цене, равной предельным издержкам. Это означает, что кривые средних и предельных издержек каждой фирмы имеют вертикальный вид при q = К: предельные издержки производства следующей единицы можно считать стремящимися к бесконечности. Если обе фирмы назначают цену Р = МС, их совокупный выпуск (Q = К1 + К2) достаточен, чтобы удовлетворить отраслевой спрос. Если фирма 1 увеличит свою цену, потребители захотят покупать товар фирмы 2, предлагающей более низкую цену. Однако половина потребителей не смогут купить продукт из-за ограниченности производственных возможностей фирмы 2. Они будут вынуждены покупать продукт у фирмы 1 по высокой цене. Фирма 1 столкнется с остаточным спросом RD1 (рис. 4.2), причем QRD1(Р) = QD(Р) – К2. По отношению к этому остаточному спросу фирма 1 будет действовать как монополист, максимизируя прибыль там, где МRrd1 – МС1. Цена фирмы 1 будет установлена на уровне Р1 > Р2 = МС, так что фирма 1 будет получать положительную экономическую прибыль, в то время как прибыль фирмы 2 останется равной нулю, несмотря на ее большую долю рынка.
Рис. 4.2. Модель Эджворта В следующий период фирма 2 опустит свою цену до уровня ниже P1 - цены первого периода фирмы 1 так, чтобы переманить покупателей фирмы 1. Однако, поскольку производственные мощности фирмы 2 ограничены, она сможет удовлетворить только две трети рыночного спроса. В этот период фирма 2 продаст в два раза больше, чем фирма 1, почти по той же цене, в результате чего прибыли фирмы 1 удвоятся. Еще через период фирмы будут постепенно по очереди снижать цены до тех пор, пока одна из фирм не установит цену Рк на уровне, при котором за счет роста объема продаж (внутри, ограничений, налагаемых производственными мощностями) ее прибыль не окажется равной прибыли при наивысшей цене Рk = Р1: 0.5(P1 - MC)K = (Pk - MC)K С этой точки зрения другая фирма может попытаться поднять цену до уровня Р1. В результате начнется новый цикл последовательного снижения цен фирмами. Таким образом, статическое равновесие с одной ценой никогда не будет достигнуто; уровень цен будет последовательно подниматься и опускаться в интервале Рк < Р <P1, ценовая война никогда не прекратится. Рассмотрим пример. Предположим, рыночный спрос выражается формулой: Qd = 100 - Р, где Qd - величина спроса, в тыс. шт.; Р - рыночная цена. Пусть на рынке действуют две фирмы, предельные издержки которых постоянны, одинаковы и равны 10. Мощности каждой фирмы ограничены объемом в 45 тыс. шт. (К1 = К2 = 45). Равновесие Бертрана в данных условиях достижимо (q1 = q2 = 45; Р = 10), но оно не является равновесием по Нэшу. Докажем это. Пусть первая фирма назначает цену P1 = 10. Ее объем предложения будет равен q1 = K1 = 45. Тогда вторая фирма может максимизировать свою прибыль по остаточному (после первой фирмы) спросу:
Максимизация прибыли обеспечивается ценой Р2 = 32.5 и объемом продаж q2 = 22,5. Вторая фирма получает прибыль π = 506,25 - это минимальная прибыль, которую может иметь вторая фирма, ориентируясь на остаточный спрос. Таким образом, стратегия «назначать цену на уровне предельных издержек» не является равновесием по Нэшу ни для одной фирмы, так как отклоняясь от этой стратегии фирма увеличивает свою прибыль. Совокупное предложение рынка в этих условиях составит: Qd = q2 + K1 = 67.5 Итак, если P1 достаточно низкая, второй фирме имеет смысл максимизировать прибыль по остаточному спросу. Ситуация меняется, если цена первой фирмы Р1 достаточно высока. Предположим, Р1 = 40. Тогда если вторая фирма назначит цену, меньшую цены первой фирмы (например, Р2 = 39), она получит весь спрос рынка: QRD2(P2 = 39) = 61 >K2. В этом случае объем остаточного спроса на товар второй фирмы превысит ее максимальный выпуск. Соответственно, объем ее продаж будет равен максимально возможному выпуску. Прибыль составит π2 = 1755 - что выше, чем если бы фирма ориентировалась на остаточный спрос. В общем виде прибыль второй фирмы (в том случае, если цена первой фирмы достаточно высока) составит:
где ε - бесконечно малая величина; АС2 - средние издержки второй фирмы. У каждой фирмы есть две возможные стратегии: 1. Максимизировать прибыль по остаточному спросу Qrdi = Qd – Kj. 2. Установить цену на уровне, ниже цены конкурента Pi = Pj – ε. Для рассматриваемого примера первая стратегия приносит фирме прибыль πi = 506,25; вторая- πi = (Pj - ε - ACi)Ki. Найдем минимальное значение P1, при котором второй фирме выгодно снижать цену. Пренебрегая бесконечно малой величиной, условие предпочтительности ценовой конкуренции составит: (Р1 - 10) 45 > 506,25. Откуда P1 > 21,25. Таким образом, ценовая конкуренция приносит большую прибыль только в том случае, если конкурент на рынке устанавливает достаточно высокую цену. Поскольку цена фирмы известна, а цена конкурента опустится достаточно низко, интервал возможных колебаний цен на рынке определится как Pi, Pj € [21,25; 32,5], где нижнее значение обеспечивается минимальным уровнем цены при выборе фирмой стратегией снижения цены, а верхнее значение представляет собой цену при выборе фирмой стратегии максимизации прибыли по остаточному спросу. Мощность играет на рынке роль фактора, ограничивающего возможности и стимулы ценовой конкуренции. Следовательно, выбор мощности играет роль предварительной договоренности фирм о масштабах ценовой конкуренции. Покажем это на примере, предположив, что мощности фирм существенно выше. Пусть K1 = K2 = 80. Тогда соответствующий интервал цен будет равен Р1, P2 € [10,71; 15]. Чем выше мощности фирм, тем уже интервал возможных цен и тем ближе цены, назначаемые фирмами на рынке, к средним издержкам. Пусть, К1 = К2 = 30. Тогда, максимизируя прибыль по остаточному спросу, фирма выберет объем продаж, равный 30 и назначит цену, равную 40, получив прибыль, равную 900. Далее, фирме выгодна ценовая конкуренция только при условии (P1 - 10)30 > 900, то есть если цена конкурента превышает 40.В данном случае получаем единственную цену рынка P1 = Р2= Р* = 40, ценовая война между фирмами исключена. Парадокс Бертрана разрешается благодаря: · - длительности взаимодействия фирм на рынке и их ориентации на долгосрочные цели; · - дифференциации продукта продавцов и приверженности марке; · - ограниченности мощности предприятий. Три названных характеристики служат важнейшими условиями, ограничивающими ценовую конкуренцию. И служат объектом стратегического выбора. Таким образом, доказана оправданность использования моделей (где стратегической переменной служит количество) в качестве инструмента анализа олигополии. Фирмы, желающие исключить ценовую войну между собой, выберут производственные мощности, равные равновесному объему выпуска в другой модели поведения олигополии - модели Курно. Модель Курно Цель модели заключается в том, чтобы показать каким образом устанавливается равновесный объем продаж на рынке, если фирма выбирает количество в зависимости от того, которое продает на рынке другая фирма. Фирмы выбирают объем продаж одновременно - обе они проводят «недальновидную» политику. Из-за этого, реакция контрагента приводит к тому, что ожидаемый фирмой выпуск контрагента может отличаться от фактического. Равновесие на рынке достигается тогда, когда ожидания каждой фирмы относительно объема выпуска конкурента реализуются. Пусть фирма 1 ожидает, что фирма 2 произведет q2 количества товара. Тогда фирма 1 решает произвести q1 единиц товара. Совокупный объем продаж отрасли составит Q = q1 + q2. Этот объем будет продан по цене Р(Q) = P(q1 + q2) Фирма 1 стремится к максимизации прибыли. Максимум прибыли достигается при таком объеме производства фирмы 1, когда ее предельные издержки равны ее предельной выручке: МС = МR, то есть:
Такое же условие максимизации прибыли можно записать и для фирмы 2. Поскольку по условию каждая фирма выбирает объем своего производства, исходя из предположения о размере выпуска другой фирмы, оптимальный объем производства фирмы 1 будет зависеть от ожидаемого объема производства фирмы 2: q1 = f(q2exp) оптимальный объем производства фирмы 2 будет зависеть от ожидаемого объема выпуска фирмы 1: q1 = h(q2exp), где f и h - функции реакции первой и второй фирм соответственно, (qiexp - ожидаемый j-й фирмой выпуск i-й фирмы, i, j = 1,2; i ≠ j). Если ожидания фирм не оправдываются, q1 ≠ q1exp q2 ≠ q2exp фирмы пересматривают как предположения, так и свой собственный объем производства в соответствии с реальным выпуском другой фирмы. В результате меняется совокупное предложение отрасли и рыночная цена. Стабильное равновесие на рынке устанавливается тогда, когда ожидаемые выпуски фирм равны их реальным объемам производства, причем реальный выпуск и является оптимальным:
Другими словами, каждая фирма выбирает такой оптимальный объем производства, какой ожидает от нее другая фирма. Такое равновесие называется равновесием Курно. Пусть функция рыночного спроса линейна и имеет вид
где а - параметр спроса; q1, q2 - объемы выпуска фирм 1 и 2. Предельные издержки фирм одинаковы, постоянны и равны МС. Тогда условие максимизации прибыли для первой и второй фирмы соответственно будет иметь вид
Отсюда функции реагирования для каждой фирмы составят:
Эти уравнения описывают все комбинации q1 и q2, которые приносят максимальную прибыль каждой фирме. Поскольку фирмы идентичны, в равновесии они будут производить одинаковое количество товара, то есть
Общий объем продаж в отрасли составит
Рис. 4.3. Модель Курно Если кривые реакции изобразить графически (рис. 4.3.), равновесие Курно достигается в точке их пересечения. Именно здесь ожидаемые объемы двух фирм совпадают с их реальными величинами. Механизм достижения равновесия приходит следующим образом. В точке А фирма 1 произведет большее количество товара, чем от нее ожидает фирма 2. В результате фирма 2 будет вынуждена сократить свой объем выпуска в следующем периоде. В то же время фирма 1 в расчете на большое количество товара фирмы 2 тоже сократит свой выпуск. Когда и эти ожидания не оправдываются, фирмы будут корректировать объемы производства до тех пор, пока не будет достигнута точка равновесия, пока их ожидания не будут оправдываться. Рассмотрим равновесие Курно для n фирм. Предположим, что на рынке действует несколько фирм, каждая из которых проводит стратегию, соответствующую предпосылкам модели. Другими словами, каждая фирма на рынке выбирает оптимальный объем производства, исходя из своих ожиданий относительно объемов производства других фирм. Если число фирм на рынке равно n, то общий объем предложения составит величину Q = q1 + q2 +…+ qn. Каждая фирма, максимизируя прибыль, будет производить такой объем, чтобы:
то есть Каждая фирма ожидает, что другие участники рынка сохраняет свой объем продаж неизменным. Поэтому с ее точки зрения изменение объема продаж на рынке совпадет с изменением ее собственных продаж, dQ = dqi. Домножим второе слагаемое в левой части на выражение PQ/PQ. Поскольку произведение
где qi/Q- доля выпуска данной фирмы в общем объеме производства отрасли, qi/Q = Y. Тогда цена на рынке и индекс Лернера монопольной власти
Эта формула показывает зависимость рыночной цены и монопольной власти фирм, действующих на рынке, от числа фирм и их рыночной доли. Если Yi стремится к нулю (ситуация свободной конкуренции), цена стремится к уровню предельных издержек: Р(Q) = МС. Если Yi = 1 (рынок монополии). Получаем формулу монопольной цены: Р(Q) = МС/[1+1/Еd]. Соответственно, промежуточные случаи расположены между этими крайними ситуациями. Таким образом, равновесие Курно позволяет связать воедино разные рыночные структуры. Модель Штакельберга В предыдущих моделях предполагалось, что фирмы обладают одинаковой рыночной силой, и их поведение определяется одновременно. Рассмотрим ситуацию, когда фирмы неодинаковы по силе, а выбор объема производства осуществляется последовательно: сначала объем производства определяется для более «сильной» фирмы, затем «слабая» фирма выбирает свою линию поведения. При этом исходим из того, что фирмы, выбирая мощность, устанавливают границы ценовой конкуренции и барьеры входа для потенциального конкурента. Модели Эджворта и Курно показывают, каким образом выбор производственной мощности влияет на ценовую конкуренцию и какие мощности выбирают фирмы, принимая решения одновременно, с тем чтобы исключить ценовую войну. Рассмотрим, какую производственную мощность должен выбрать лидер, учитывая будущую реакцию другой фирмы (или фирм) на свои действия. Пусть фирмы выбирают, какое количество товара производить, а цена устанавливается рынком. Предположим, фирма 1 является лидером на рынке и принимает решение относительно величины выпуска независимо, в то время как фирма 2 корректирует свое поведение, исходя из того выбора, который сделала фирма 1. Тогда цель фирмы 2 заключается в том, чтобы максимизировать прибыль при заданном объеме производства фирмы 1:
Реакция фирмы 2 состоит в максимизации прибыли q2 = h(q1) В случае линейной функции спроса Р = a - q1 – q2 функция реакции фирмы 2, как было показано выше,
Рассмотрим поведение фирмы-лидера (фирма 1). Фирма-лидер, знает, что ее выбор объема производства оказывает влияние на размер выпуска фирмы 2, а следовательно, на общий объем предложения отрасли, рыночную цену и в конечном итоге прибыль самой фирмы-лидера. Поэтому для нее условие максимизации прибыли принимает вид:
То есть
В примере условие максимизации прибыли лидера будет выглядеть:
Откуда
Общий объем предложения отрасли равен:
Прибыль лидера в модели Штакельберга вдвое превышает прибыль последователя.
Рис. 4.4. Модель Штакельберга Стратегическое поведение лидера, учитывающее будущую реакцию конкурента на рынке, приносит ему «преимущество первого хода». Применение той или иной модели зависит от характеристик рынка и возможностей фирмы влиять на рыночную цену или объем выпуска. Модели Курно и Штакельберга применяются при исследованиях рынков, когда у фирм существуют фиксированные производственные планы, так что относительно трудно изменить количество выпускаемого продукта, если план уже принят. Это характерно для отраслей с длительным сроком изготовления товара (тяжелая промышленность, самолетостроение, производство уникального оборудования, судостроение и т. д.), а также для тех отраслей, где фирмам необходимо инвестировать значительные средства в специализированное оборудование для сбыта данного товара (например, строительство крупного универмага). На таких рынках изменение цен товаров более вероятно, чем изменение объемов продаж. Модели Бертрана и Эджворта применяются в тех случаях, когда фирмам сложнее корректировать принятые цены. Примерами могут служить продажи по каталогам, тендеры, аукционы, причем преимущественно в отраслях, производящих товары потребительского назначения. В этом случае, напротив, изменение цен менее вероятно, чем изменение объемов продаж.
Поиск по сайту: |
 (4.4)
(4.4) (4.5)
(4.5) (4.6)
(4.6) (4.7)
(4.7)
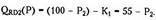

 (4.8)
(4.8)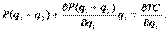 (4.9)
(4.9) (4.10)
(4.10) (4.11)
(4.11) (4.12)
(4.12) (4.13)
(4.13) (4.14)
(4.14) (4.15)
(4.15)
 (4.16)
(4.16) (4.17)
(4.17)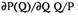 представляет собой эластичность рыночного спроса Ed, условие максимизации прибыли фирмы можно записать в виде:
представляет собой эластичность рыночного спроса Ed, условие максимизации прибыли фирмы можно записать в виде: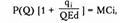 (4.18)
(4.18)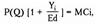 (4.19)
(4.19) (4.20)
(4.20) (4.21)
(4.21) (4.22)
(4.22) (4.23)
(4.23)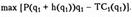 (4.24)
(4.24) (4.25)
(4.25) (4.26)
(4.26)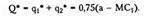 (4.27)
(4.27)