 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Модель обслуживания машинного парка ⇐ ПредыдущаяСтр 7 из 7
Модель обслуживания машинного парка представляет собой модель замкнутой системы массового обслуживания. До сих пор рассматривались только такие системы массового обслуживания, для которых интенсивность Например, обслуживается машинный парк, состоящий из N машин, бригадой R механиков В рассматриваемой модели емкость источника требований следует считать ограниченной. Входящий поток требований исходит из ограниченного числа эксплуатируемых машин Таким образом, в замкнутой системе массового обслуживания входящий поток требований формируется из выходящего. Состояние Если
Система алгебраических уравнений, описывающих работу замкнутой СМО в стационарном режиме, выглядит следующим образом:
Решая данную систему, находим вероятность k-гo состояния:
Величина P0 определяется из условия нормирования - среднее число требований в очереди на обслуживание:
- среднее число требований, находящихся в системе (на обслуживании и в очереди)
- среднее число механиков (каналов), «простаивающих» из-за отсутствия работы
- коэффициент простоя обслуживаемого объекта (машины) в очереди
- коэффициент использования объектов (машин)
- коэффициент простоя обслуживающих каналов (механиков)
- среднее время ожидания обслуживания (время ожидания обслуживания в очереди)
Пример. Пусть для обслуживания десяти персональных компьютеров (ПК) выделено два инженера одинаковой производительности. Поток отказов (неисправностей) одного компьютера - пуассоновский с интенсивностью Возможны следующие варианты организации обслуживания: - оба инженера обслуживают все десять компьютеров, так что при отказе ПК его обслуживает один из свободных инженеров, в этом случае - каждый из двух инженеров обслуживает по пять закрепленных за ним ПК. В этом случае Необходимо выбрать наилучший вариант организации обслуживания ПК. Решение 1. Вычислим параметр обслуживания
2. Приведенная интенсивность
3. Вычислим вероятностные характеристики СМО для двух вариантов организации обслуживания ПК.
Вариант 1
1. Определим вероятности состояний системы:
Учитывая, что
Откуда Тогда
- Определим среднее число компьютеров в очереди на обслуживание:
- Определим среднее число ПК, находящихся в системе (на обслуживании и в очереди):
- Определим среднее число инженеров, простаивающих из-за отсутствия работы:
- Коэффициент простоя персонального компьютера в очереди следующий:
- Коэффициент использования компьютеров определяется по формуле:
- Коэффициент простоя обслуживающих инженеров рассчитывается по формуле:
- Среднее время ожидания ПК обслуживания
Вариант 2
Определим вероятности состояний системы:
Откуда P0 = 0,199. Тогда
- Среднее число компьютеров в очереди на обслуживание равно:
- Среднее число компьютеров, находящихся на обслуживании и в очереди рассчитывается по формуле:
- Среднее число инженеров, простаивающих из-за отсутствия работы:
- Коэффициент простоя персонального компьютера в очереди:
- Коэффициент использования компьютеров:
- Коэффициент простоя обслуживающих инженеров:
- Среднее время ожидания ПК обслуживания:
Сведем полученные результаты по двум вариантам в следующую таблицу:
Таким образом, в варианте 1 каждый компьютер стоит в очереди в ожидании начала его обслуживания приблизительно 0,142 части рабочего времени, что меньше этого показателя при варианте 2 организации работ. Далее в варианте 1 вероятность того, что ПК и любой момент времени будет работать выше, чем в варианте 2, и равна
Поиск по сайту: |
 входящего потока заявок не зависит от состояния системы. В этом случае источник заявок является внешним по отношению к СМО и генерирует неограниченный поток требований. Рассмотрим системы массового обслуживания, для которых
входящего потока заявок не зависит от состояния системы. В этом случае источник заявок является внешним по отношению к СМО и генерирует неограниченный поток требований. Рассмотрим системы массового обслуживания, для которых  , причем каждая машина может обслуживаться только одним механиком. Здесь машины являются источниками требований (заявок на обслуживание), а механики - обслуживающими каналами. Неисправная машина после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание. Очевидно, что интенсивность
, причем каждая машина может обслуживаться только одним механиком. Здесь машины являются источниками требований (заявок на обслуживание), а механики - обслуживающими каналами. Неисправная машина после обслуживания используется по своему прямому назначению и становится потенциальным источником возникновения требований на обслуживание. Очевидно, что интенсивность 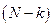 и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k).
и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k). Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным.
Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным. системы характеризуется общим числом требований, находящихся на обслуживании и в очереди, равным k. Для рассматриваемой замкнутой системы, очевидно,
системы характеризуется общим числом требований, находящихся на обслуживании и в очереди, равным k. Для рассматриваемой замкнутой системы, очевидно,  . При этом если система находится в состоянии
. При этом если система находится в состоянии 

 (40)
(40) (41)
(41) полученных результатов по формулам (41) для
полученных результатов по формулам (41) для  ,
,  (42)
(42) (43)
(43) (44)
(44) (45)
(45) (46)
(46) (47)
(47) (48)
(48) . Время обслуживания ПК подчиняется показательному закону. Среднее время обслуживания одного ПК одним инженером составляет:
. Время обслуживания ПК подчиняется показательному закону. Среднее время обслуживания одного ПК одним инженером составляет:  час.
час.









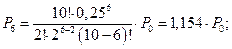




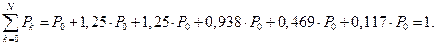
 и используя результаты расчета
и используя результаты расчета  , вычислим
, вычислим  :
:

















 час.
час.















 час.
час.



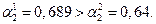 Очевидно, вариант 1 организации работ по обслуживанию ПК эффективнее, чем вариант 2.
Очевидно, вариант 1 организации работ по обслуживанию ПК эффективнее, чем вариант 2.