 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
С экспоненциальным распределением длительности обслуживания
Простейшей одноканальной моделью с вероятностными входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид
где Плотность распределения длительностей обслуживания:
где Потоки заявок и обслуживание простейшие. Пусть система работает с отказами. Необходимо определить абсолютную и относительную пропускную способность системы. Представим данную систему массового обслуживания в виде графа (рис. 4.1), у которого имеются два состояния:
Рис. 4.1. Граф состояний одноканальной СМО с отказами
Обозначим вероятности состояний:
Система линейных дифференциальных уравнений (3) имеет решение с учетом нормировочного условия
Нетрудно убедиться, что для одноканальной СМО с отказами вероятность Действительно,
По истечении большого интервала времени (при
Зная относительную пропускную способность, легко найти абсолютную. Абсолютной пропускной способностью (А) называется среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:
Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал занят»:
Данная величина Pотк может быть интерпретирована как средняя доля необслуженных заявок среди поданных. Пример. Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания (ЕО) для мойки автомобилей. Заявка - автомобиль, прибывший в момент, когда пост занят, - получает отказ в обслуживании. Интенсивность потока автомобилей - относительной пропускной способности q; - абсолютной пропускной способности А; - вероятности отказа Pотк ; Сравнить фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали один за другим без перерыва. Решение 1. Определим интенсивность потока обслуживания:
2. Вычислим относительную пропускную способность:
Величина q означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост ЕО автомобилей. 3. Абсолютную пропускную способность определим по формуле:
Это означает, что система (пост ЕО) способна осуществить в среднем 0,356 обслуживания автомобилей в час. 4. Вероятность отказа:
Это означает, что около 65% прибывших автомобилей на пост ЕО получат отказ в обслуживании. 5. Определим номинальную пропускную способность системы:
(автомобилей в час). Оказывается, что Аном в 1,5 раза
Поиск по сайту: |
 (1)
(1) - интенсивность поступления заявок в систему.
- интенсивность поступления заявок в систему. (2)
(2)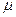 - интенсивность обслуживания
- интенсивность обслуживания - канал свободен (ожидание);
- канал свободен (ожидание);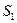 - канал занят (идет обслуживание заявки).
- канал занят (идет обслуживание заявки).
 - вероятность состояния «канал свободен»;
- вероятность состояния «канал свободен»;  - вероятность состояния «канал занят». По размеченному графу состояний (рис. 4.1) составим систему дифференциальных уравнений Колмогорова для вероятностей состояний:
- вероятность состояния «канал занят». По размеченному графу состояний (рис. 4.1) составим систему дифференциальных уравнений Колмогорова для вероятностей состояний: (3)
(3) Решение данной системы называется неустановившимся, поскольку оно непосредственно зависит от t и имеет вид:
Решение данной системы называется неустановившимся, поскольку оно непосредственно зависит от t и имеет вид: (4)
(4)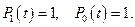 (5)
(5) - вероятность того, что в момент t канал свободен и заявка, пришедшая к моменту t, будет обслужена, а следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно
- вероятность того, что в момент t канал свободен и заявка, пришедшая к моменту t, будет обслужена, а следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно  , (6)
, (6) ) достигается стационарный (установившийся) режим:
) достигается стационарный (установившийся) режим: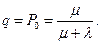 (7)
(7) (8)
(8) (9)
(9) (автомобиль в час). Средняя продолжительность обслуживания - 1,8 часа. Поток автомобилей и поток обслуживании являются простейшими. Определить в установившемся режиме предельные значения:
(автомобиль в час). Средняя продолжительность обслуживания - 1,8 часа. Поток автомобилей и поток обслуживании являются простейшими. Определить в установившемся режиме предельные значения: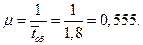



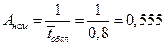
 больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания.
больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания.