 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Многоканальная система массового обслуживания с ожиданием
Рассмотрим многоканальную систему массового обслуживания с ожиданием. Процесс массового обслуживания при этом характеризуется следующим: входной и выходной потоки являются пуассоновскими с интенсивностями В установившемся режиме функционирование многоканальной СМО с ожиданием и неограниченной очередью может быть описано с помощью системы алгебраических уравнений:
Решение системы уравнений (32) имеет вид
где
Решение будет действительным, если выполняется следующее условие: Вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием и неограниченной очередью определяются по следующим формулам: - вероятность того, что в системе находится n клиентов на обслуживании, определяется по формулам (33) и (34); - среднее число клиентов в очереди на обслуживание
- среднее число находящихся в системе клиентов (заявок на Обслуживание и в очереди)
- средняя продолжительность пребывания клиента (заявки на обслуживание) в очереди
- средняя продолжительность пребывания клиента в системе
Пример. Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации. Поток неисправных механизмов, прибывающих в мастерскую, - пуассоновский и имеет интенсивность Требуется вычислить следующие предельные значения вероятностных характеристик системы: - вероятности состояний системы; - среднее число заявок в очереди на обслуживание; - среднее число находящихся в системе заявок; - среднюю продолжительность пребывания заявки в очереди; - среднюю продолжительность пребывания заявки в системе. Решение 1. Определим параметр потока обслуживаний
2. Приведенная интенсивность потока заявок
при этом Так как 3. Вычислим вероятности состояний системы:
4. Вероятность отсутствия очереди у мастерской
5. Среднее число заявок в очереди на обслуживание
6. Среднее число находящихся в системе заявок
7. Средняя продолжительность пребывания механизма в очереди на обслуживание
8. Средняя продолжительность пребывания механизма в мастерской (в системе)
Поиск по сайту: |
 и
и 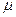 соответственно; параллельно обслуживаться могут не более S клиентов. Система имеет S каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна -
соответственно; параллельно обслуживаться могут не более S клиентов. Система имеет S каналов обслуживания. Средняя продолжительность обслуживания одного клиента равна - 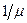 .
.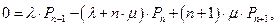 при
при 
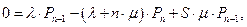 при
при  (32)
(32)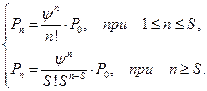 (33) (34)
(33) (34) . (35)
. (35)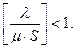
 (36)
(36) (37)
(37)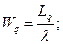 (38)
(38) (39)
(39)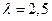 механизма в сутки, среднее время ремонта одного механизма распределено по показательном у закону и равно
механизма в сутки, среднее время ремонта одного механизма распределено по показательном у закону и равно 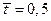 сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно.
сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно.


 , то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.
, то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.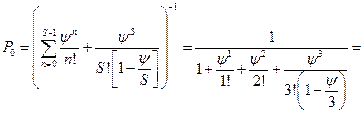
 ;
;
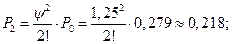
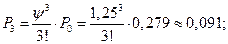


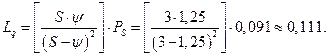
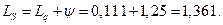
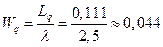 суток.
суток.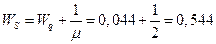 суток.
суток.