 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Выделение критического множителя ⇐ ПредыдущаяСтр 4 из 4
Правило.Чтобы раскрыть неопределенность вида
Примеры Найти пределы функций: 1.
2.
Преобразование иррациональных выражений Правило.Чтобы раскрыть неопределенность вида − перенести иррациональность из числителя в знаменатель, или из знаменателя в числитель, домножив дробь на сопряженные выражения, − либо сделать замену переменной. Замечание. Если под знаком предела делается замена переменной, то все величины, входящие под знак предела, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной.
Примеры Найти пределы функций: 1.
2.
3.
4.
Применение первого замечательного предела Правило.Для раскрытия неопределенности вида
где
Примеры Найти пределы функций: 1.
2.
4.
Применение эквивалентных бесконечно малых величин Правило.Для раскрытия неопределенности вида
Примеры Найти пределы функций: 1.
2.
3.
4.
Неопределенности вида Если Если Правило.Неопределенности вида
Примеры Найти пределы функций:
Неопределенности вида Пусть функция имеет вид:
Если при
или
Примеры Найти пределы функций: 1.
2.
3.
Если при Если Для раскрытия неопределенностей вида
Примеры Найти пределы функций: 1.
2.
В заключение отметим, что в дальнейшем будут рассмотрены более эффективные методы вычисления пределов функций, основанные на использовании понятия производной.
Упражнения Односторонние пределы. Найти пределы: 1.
2.
Непосредственное вычисление пределов. Найти пределы: 3. 4. 5.
Раскрытие неопределенности 6. 7. 8. 9.
Раскрытие неопределенности 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
Раскрытие неопределенностей 21. 22. 23. 24.
Раскрытие неопределенности 25. 26. 27. 28.
Поиск по сайту: |
 , заданную отношением двух многочленов, надо и в числителе и в знаменателе выделить критический множитель и сократить на него дробь.
, заданную отношением двух многочленов, надо и в числителе и в знаменателе выделить критический множитель и сократить на него дробь. ;
; ;
;

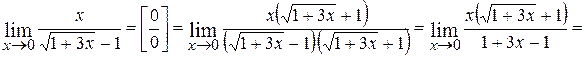
 ;
;
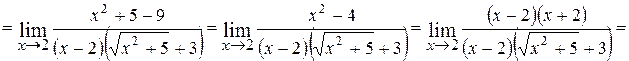
 ;
;

 ;
;
 .
. или
или  ,
, и
и  .
. ;
; ;
;
 .
.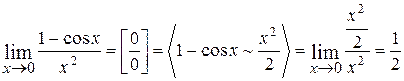 ;
; ;
; ;
;
 .
. и
и 
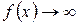 и
и  при
при 
 , то их разность
, то их разность  представляет собой неопределенность вида
представляет собой неопределенность вида  и
и  − это неопределенность вида
− это неопределенность вида  или
или 

 .
. ,
,  ,
, 
 .
. , а
, а  ;
; 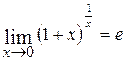 ;
;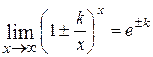 ;
;  .
. ;
; ;
; ;
;
 , а
, а  , то имеем неопределенность вида
, то имеем неопределенность вида  и
и  .
. ;
; ;
; ; Ответ:
; Ответ:  ;
; ; Ответ:
; Ответ:  ;
; ; Ответь:
; Ответь: 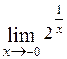 ; Ответ: 0.
; Ответ: 0. ; Ответ: 15;
; Ответ: 15; ; Ответ:
; Ответ:  .
. ; Ответ: 0.
; Ответ: 0. ; Ответ: 0;
; Ответ: 0;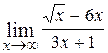 ; Ответ: -2;
; Ответ: -2;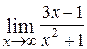 ; Ответ:
; Ответ:  ;
;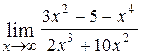 ; Ответ:
; Ответ:  ; Ответ:
; Ответ:  ;
; ; Ответ: -2;
; Ответ: -2; ; Ответ:
; Ответ:  ;
; ; Ответ:
; Ответ:  ;
; ; Ответ: -12;
; Ответ: -12; ; Ответ:
; Ответ:  .
. ; Ответ:
; Ответ:  ; Ответ:
; Ответ:  ;
; ; Ответ:
; Ответ:  ; Ответ:
; Ответ:  ; Ответ:
; Ответ:  .
. . Найти пределы:
. Найти пределы: ; Ответ:
; Ответ:  ;
;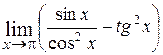 ; Ответ:
; Ответ:  ; Ответ: 0;
; Ответ: 0;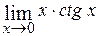 ; Ответ: 1.
; Ответ: 1. . Найти пределы:
. Найти пределы: ; Ответ:
; Ответ:  ;
;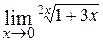 ; Ответ:
; Ответ:  ;
;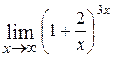 ; Ответ:
; Ответ:  ;
; ; Ответ:
; Ответ: 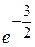 .
.