 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Предел числовой последовательности
По аналогии с пределом функции в бесконечно удаленной точке вводится понятие предела последовательности.
Определение. Число а называется пределом числовой последовательности
Обозначают:
Говорят также, что последовательность Например, последовательность
с общим членом
имеет предел
Бесконечно большие функции Определение. Функция
Например, бесконечно большими функциями (б.б.ф.) являются:
Различают частные случаи б.б.ф., когда, начиная с некоторого момента, б.б.ф. возрастая, принимает только положительные значения или, убывая, принимает только отрицательные значения. Записывают это следующим образом:
Например,
Бесконечно малые функции Определение. Функция
Бесконечно малые функции (б.м.ф.) обозначают малыми греческими буквами α(х), β(х) и т.д. Например,
Между бесконечно большими и бесконечно малыми функциями существует простая связь, устанавливаемая следующей теоремой.
Теорема. Если функция
Справедлива и обратная теорема: величина, обратная всякой бесконечно большой, будет бесконечно малой. Например,
Связь между функцией, ее пределом и бесконечно малой функцией Сравнивая между собой определения предела функции в точке с определением бесконечно малой функции, можно заметить, что разность между функцией и ее пределом является величиной бесконечно малой. Утверждение этого факта формулируют в двух теоремах − прямой и обратной.
Теорема (прямая). Если функция
Теорема (обратная). Если функцию
Поиск по сайту: |
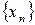 , если для любого
, если для любого 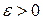 найдется такое натуральное число
найдется такое натуральное число 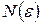 , что при всех
, что при всех 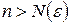 выполняется неравенство
выполняется неравенство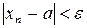 .
.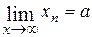 или
или 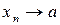 при
при 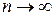 .
.
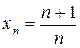
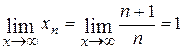 .
.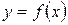 называется бесконечно большой при
называется бесконечно большой при 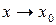
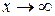 ), если
), если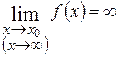 или
или 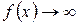 при
при 
 .
.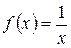 при
при 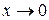 ;
; при
при  ;
;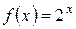 при
при 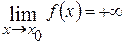 ,
, 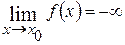 .
.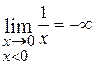 ,
, 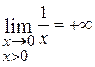 .
.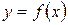 называется бесконечно малой при
называется бесконечно малой при 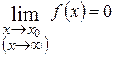 .
. при
при 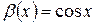 при
при 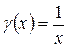 при
при  есть бесконечно малая функция при
есть бесконечно малая функция при 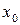
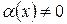 , то обратная величина
, то обратная величина  является бесконечно большой функцией при
является бесконечно большой функцией при  при
при 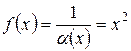 при
при 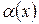 , т.е. если
, т.е. если 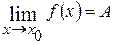 , то
, то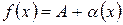 .
.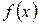 может быть как больше, так и меньше своего предела.
может быть как больше, так и меньше своего предела. .
.