 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Второй замечательный предел. Можно доказать, что функция
Можно доказать, что функция
при
Число е иррациональное, его приближенное значение равно 2,72 ( Дадим другое выражение для числа е. Полагая
Оба равенства называют вторым замечательным пределом. С помощью числа е удобно выражать многие пределы. Замечание. Показательная функция вида
называется экспоненциальной, употребляется также обозначение
Эквивалентные бесконечно малые Пусть Если Обозначается: Например, Для эквивалентных бесконечно малых справедливы следующие свойства: 1. Если 2. Если 3. Если Последнее свойство означает, что при нахождении предела, можно бесконечно малые, стоящие в числителе или в знаменателе или в обоих, заменять эквивалентными им величинами, в частности, более простыми. Такой прием часто применяют при вычислении пределов функций. Ниже приведены важнейшие эквивалентности, которыми пользуются при вычислении пределов функций:
Вычисление пределов функций. Раскрытие неопределенностей Правило.Для вычисления предела функции Для всех основных элементарных функций в любой точке их области определения имеет место равенство
Примеры Найти пределы функций:
2.
3.
4.
5.
При вычислении пределов функций формальная подстановка вместо х предельного значения Например, Выражения вида Вычисление предела функции в этих случаях называют раскрытием неопределенности. Рассмотрим правила раскрытия таких неопределенностей.
Неопределенность вида Если
Правило.Чтобы раскрыть неопределенность вида Например,
Рассмотрим дробно−рациональную функцию
представляющую собой отношение двух многочленов относительно х степеней m и n соответственно, и исследуем поведение этой функции при При нахождении предела данной функции при
Из этого следует, что предел отношения двух многочленов при
Примеры Найти пределы функций: 1.
2.
3.
Неопределенность вида Если требуется найти Рассмотрим возможные приемы раскрытия такой неопределенности.
Поиск по сайту: |

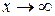 стремится к числу е:
стремится к числу е: .
. …). Число е служит основанием натуральных логарифмов (
…). Число е служит основанием натуральных логарифмов (  ) и играет важную роль в математике.
) и играет важную роль в математике. (
(  , т.к.
, т.к.  .
.
 .
. и
и  − бесконечно малые функции при
− бесконечно малые функции при  (или
(или  и
и  .
.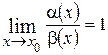 , то
, то 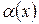 и
и  называются эквивалентными бесконечно малыми (при
называются эквивалентными бесконечно малыми (при  .
. при
при 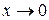 , т.к.
, т.к.  .
. .
. при
при  при
при  и
и  при
при  , т.е. предел отношения двух бесконечно малых величин равен пределу отношения эквивалентных им бесконечно малых.
, т.е. предел отношения двух бесконечно малых величин равен пределу отношения эквивалентных им бесконечно малых.





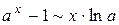


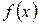 в точке
в точке  или при
или при  .
.
 ;
; ;
; ;
; .
.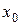 часто приводит к неопределенным выражениям вида:
часто приводит к неопределенным выражениям вида:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. или
или  .
.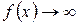 и
и  при
при  представляет собой неопределенность вида
представляет собой неопределенность вида 
 .
. (
(  ),
), , если
, если  ;
;
 , если
, если  ;
;
 , если
, если  .
.
 ;
; ;
; .
. , где
, где  − бесконечно малые функции при
− бесконечно малые функции при  , то в этом случае вычисление предела называют раскрытием неопределенности вида
, то в этом случае вычисление предела называют раскрытием неопределенности вида