 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Возможности формализации деятельности оператора
Применение математических методов в инженерной психологии основано во многих случаях на формализации деятельности оператора. В самом общем случае под формализацией (от лат. forma — вид, образ) понимается уточнение содержания познания, осуществляемое посредством того, что изучаемому объекту (в инженерной психологии — деятельности оператора) определенным образом сопоставляются некоторые материальные конструкции, обладающие относительно устойчивым характером и позволяющие в силу этого выявлять и фиксировать существенные и закономерные стороны рассматриваемых объектов. Особенность формализации как гносеологического приема состоит в том, что совершающееся с ее помощью выявление и уточнение содержания происходит через выявление и фиксацию его формы. Во всякой формализации всегда присутствует момент огрубления живой, развивающейся действительности. Однако это огрубление является необходимой стороной процесса познания. Основное значение для формализации имеют знаки специального характера, в частности, применяемые в математике. Проведение формализации всегда сопровождается противоречием между формой и содержанием. Опыт показывает, что если формализуется достаточно богатая содержанием теория, область научного знания (например, деятельность оператора), то она не может быть полностью отображена в формальной системе; в этой области всегда остается невыявленный, неформализуемыи остаток. Это несоответствие между формализацией и формализуемым содержанием выступает в качестве внутреннего источника развития формально-логических средств науки. Преодоление указанного противоречия происходит путем построения новых формальных систем, в которых формализуется часть того, что не было учтено при предшествующих формализациях. Таким образом осуществляется все более глубокая формализация содержания, никогда, однако, не достигающая абсолютной полноты*. Рассмотренные общефилософские и общеметодологические проблемы формализации научного знания имеют непосредственное отношение к инженерной психологии. Именно в ней открываются особенно большие возможности для формализации деятельности человека. Этому способствуют следующие обстоятельства [77]. В изучаемой здесь деятельности человек решает ограниченный круг технических задач, а его действия зачастую оказываются детерминированными извне техническими условиями. Помимо этого для операторской деятельности отбирается определенный круг людей, психофизиологические показатели которых отвечают соответствующим требованиям. Оба эти обстоятельства способствуют как ограничению числа существующих психологических переменных, определяющих поведение операторов, так и уменьшению различий в их поведении. Все это и дает основание для формализованного описания психологических закономерностей деятельности оператора. Формализация деятельности оператора, как отмечается в [207], предполагает в первую очередь математическое моделирование его трудового процесса. В общем случае модель любой деятельности может быть представлена в виде набора взаимосвязанных между собой частных моделей. При моделировании необходимо учитывать форму и тип труда (управление системой, техническое обслуживание, ремонт и т. п.); составляющие трудовой процесс операции, их взаимосвязь, точность и время выполнения; влияние на них направленности деятельности, дефицита времени, внешних условий и многих других факторов. Применяемые на практике модели можно классифицировать по функциональному назначению (модели информационного поиска [62], принятия решений [17], значащих переживаний [77], приобретения и утраты навыков [10], технической диагностики и устранения неисправностей [17] и др.) и принципу построения {информационные, игровые, структурно-алгоритмические и пр.). Приведенные модели, классифицированные по функциональному назначению, являются частными моделями, отображающими либо отдельные стороны деятельности, либо ее отдельные количественные характеристики (точность, надежность, производительность и т. п.), но не моделируют профессиональную деятельность в целом как специфическое сложное явление. Некоторые из этих моделей будут рассмотрены при изучении соответствующих разделов. Полная модель деятельности человека может быть получена лишь на основе комбинированного использования частных моделей с учетом специфики связи между ними, обусловленными психофизиологическими возможностями человека и характерными для данной системы условиями его деятельности. В таких моделях возможности формализации, как правило, меньше по сравнению с частными моделями. В них обычно остается не учитываемый, не формализуемый остаток, поэтому полные модели являются большим огрублением действительности, чем частные модели. Однако это обстоятельство не может служить основанием для отказа от формализации деятельности оператора. Важно только учитывать степень огрубления и с учетом этого применять созданные модели на практике и делать соответствующие выводы. Наличие же неформализуемого остатка является обычно стимулом для дальнейшего совершенствования разработанных моделей. Разработка математических моделей деятельности оператора является важнейшим направлением применения математических методов в инженерной психологии. Анализ деятельности человека в СЧМ показывает, что современный уровень развития отдельных математических методов и недостаточная степень познания психофизиологических и интеллектуальных характеристик, а также поведенческих мотивов человека не позволяют в настоящее время предложить универсального метода формализации, адекватно описывающего все эти процессы в деятельности человека. Поэтому для описания и оценки деятельности человека в инженерной психологии используется большое число разнообразных математических методов. В связи с этим выбор математического аппарата и построения на его основе адекватной математической модели становится самостоятельной проблемой. Чтобы уменьшить затруднения, возникающие при выборе подходящей модели, стремятся каким-то образом классифицировать уже известные модели, методы их построения и анализа, а также определить возможные области их применения. Одна из таких классификаций, основанная на делении моделей на частные и общие, рассмотрена выше. Другие подходы к классификации математических моделей приведены в работах [40, 107, 178]. Однако эти классификации несколько громоздки и не всегда достаточно информативны, что затрудняет их практическое использование. Одной из наиболее полных и пригодных для практического использования является классификация, предложенная А.В. Кудрявцевым [83]. Она приведена в табл. 8.1. В этой классификации выделены два основных класса моделей операторской деятельности: модели конкретной задачи и модели оператора (класса задач). Модели первого класса нестабильны, поскольку изменяются от задачи к задаче даже для одного режима работы оператора. В то же время эти модели довольно универсальны за счет более широкой сферы применения. Отмеченных недостатков в определенной мере лишены модели оператора, однако каждая из них (кроме, пожалуй, структурно-алгоритмических) может быть эффективно использована только в своей специфической области. Для построения моделей деятельности оператора, как следует из табл. 8.2, может быть использован различный математический аппарат. Таблица 8.1
Классификация математических моделей операторской деятельности
Таблица 8.2
Возможности применения математических методов в инженерной психологии
К математическим методам в инженерной психологии предъявляются следующие требования: размерность (описание процессов управления со многими неизвестными), динамичность (учет фактора времени), неопределенность (учет случайных, вероятностных составляющих в деятельности оператора), факторностъ (учет специфических особенностей поведения человека, например, напряженности, эмоций и т. п.), описа-тельность (возможность описания внутренних, психофизиологических механизмов деятельности человека). Кроме того, применяемые методы должны допускать возможность описания деятельности человека и функционирования машины с единых позиций, с помощью единых показателей и характеристик [196]. Сравнительная характеристика различных методов приведена в табл. 8.2. Из этой таблицы видно, что метод, одинаково хорошо учитывающий все характеристики деятельности оператора, практически отсутствует. Каждый из рассмотренных методов оптимален лишь по одной — двум характеристикам, иными словами, удачно описывает лишь определенные стороны деятельности оператора. Поэтому при решении инженерно-психологических задач очень часто приходится применять комбинацию тех или иных методов. Это можно сделать, воспользовавшись данными табл. 8.1. и 8.2. Рассмотрим более подробно возможности и особенности применения различных математических методов, перечисленных в этих таблицах, для построения моделей деятельности оператора.
8.3. Математическое моделирование деятельности
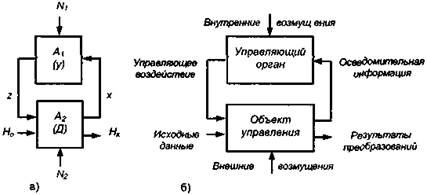
Многие из моделей, перечисленные в табл. 8.1. и прежде всего модели первого вида (модели задачи) строятся на использовании структурного подхода. Под ним в общем случае понимается описание (с помощью определенной системы символов и правил их комбинаций) взаимосвязей между различными сторонами (элементами) изучаемого явления. В общей психологии разработан ряд моделей для структурного описания восприятия, памяти, принятия решения, процессов коммуникации и т. п. [92]. Широкое применение структурный подход находит и в инженерной психологии. В основе его лежит представление деятельности оператора в виде определенной последовательности выполняемых действий. На этой основе базируется, например, обобщенный структурный метод определения надежности оператора, к числу структурных относятся и многие из расчетных методов определения времени решения задачи оператором, на базе структурного подхода осуществляется алгоритмическое описание и анализ деятельности оператора, разрабатываются структурно-алгоритмические, сетевые и автоматные модели деятельности оператора. Дадим им краткую характеристику. Применение в инженерной психологии теории автоматов и построение на ее основе моделей деятельности оператора основано на представлении ее как процесса функционирования конечного цифрового (дискретного) автомата [83, 174]. Под ним понимается математическая модель различного рода систем, которые принимают, хранят и перерабатывают в дискретном времени дискретную информацию. Такую модель можно применять, если деятельность оператора представляет собой дискретный стохастический процесс, состоящий из отдельных управляющих воздействий, формируемых на основании поступающей на сенсорные входы человека информации. Поэтому автоматные модели являются удобным средством представления и описания деятельности управляющего типа. Из абстрактной теории автоматов известно, что процесс выполнения алгоритма (в данном случае — деятельности оператора) математически может быть представлен композицией двух абстрактных автоматов: управляющего и операционного (рис. 8.3). Операционный автомат A2 непосредственно осуществляет необходимые преобразования, а управляющий автомат А1 управляет этими процессами в соответствии с заложенной программой, исходными данными Н0 и случайными внутренними N1 (например, ошибки оператора) и внешними N2 факторами, оказывающими влияние на временные, точностные и надежностные характеристики деятельности. Такой подход полностью соответствует общекиберяетической модели деятельности.
Рис. 8.3. Композиционная автоматная (а) и общекибернетическая (б) модели деятельности оператора.
Деятельность оператора как процесс функционирования дискретного абстрактного автомата может быть представлена следующим образом. Афферентный (от лат. afferens — приносящий)поток дискретной информации х (считывание показаний приборов, восприятие команд и т. п.), поступающий на вход оператора, переводит его как некоторую управляющую систему из состояния y(t) в состояние y(t+1). Результатом такого преобразования является дискретный стохастический поток эфферентности (от лат. efferens — выносящий) информации z (нажатие кнопки, установка переключателей, доклад и т. д.); при этом система переходит в новое состояние. Данный процесс циклически повторяется при переходе СЧМ из исходного состояния Н0 в требуемое Нk, то есть реализуется функция управления
где D — совокупная деятельность, которую нужно совершить в системе для перевода ее из состояния Н0 в состояние Hk. Автоматное представление деятельности оператора предполагает ее ярко выраженный дискретный характер. Это приводит к важному заключению о принципиальной допустимости декомпозиции математического описания деятельности оператора. Декомпозиция операционного автомата позволяет перейти от решения задачи отображения (8.3) в общем виде к описанию отдельных подавтоматов, характеризующих элементарные действия оператора, что значительно проще. При этом используются промежуточные результаты преобразований Hi-1––––––––>Hi. Зная входные сигналы автомата в целом или его отдельных подавтоматов и их функции переходов, можно описать их реакции (действия оператора). В простейших случаях автоматные модели строятся на основе детерминированных абстрактных автоматов, в более сложных случаях — на основе вероятностных автоматов, функционирование которых в каждом такте работы описывается вероятностными законами. Автоматные модели деятельности оператора обладают рядом достоинств, среди которых следует отметить возможность в равной степени описания как машинного, так и человеческого звена в системе «человек-машина», простоту построения модели, возможность ее сопряжения с моделями других типов. В то же время этим моделям присущ и ряд недостатков: описание деятельности с позиций бихевиоризма (от лат. behavior — поведение), т. е. в основе модели лежит простейшая поведенческая формула «стимул-реакция», поэтому она не может претендовать на полную адекватность описания реальной деятельности, поскольку в ней выпадает ее существенный компонент, связанный с высшей нервной деятельностью человека, его сознанием и мышлением. Поэтому применение автоматных моделей ограничено лишь теми видами деятельности управляющего типа, имеющими жестко алгоритмический характер. Возможности модели могут быть расширены путем применения вероятностных моделей и имитационного моделирования с помощью ЭВМ. На базе структурного подхода может быть построена целая группа моделей, условно называемых сетевыми. В основу их построения положены те или иные виды сетей. Наиболее полно разработаны модели, в основу которых положены традиционные методы сетевого планирования и управления (СПУ). Для построения сетевой модели деятельность оператора разбивается на ряд отдельных действий, имеющих вполне определенный смысл, например, нажатие кнопки, включение тумблера, движение руки к органу управления, перемещение взгляда, опознание характеристики объекта и т. п. На языке сетевых моделей эти действия называются работами, а моменты их завершения — событиями. Каждая работа в конечном итоге должна быть охарактеризована двумя параметрами — математическим ожиданием и дисперсией продолжительности (времени выполнения) работы. Общее время решения задачи оператором равно продолжительности критического пути. В таком виде модель используется для априорной оценки времени решения задачи оператором, а также для описания и оптимизации групповой деятельности операторов [27, 61]. Основным достоинством сетевой модели является возможность учета последовательно-параллельного характера выполнения отдельных действий оператором (группой операторов). Остальные достоинства и недостатки такие же, как у автоматных моделей. Принципиально новым подходом в теории и практике сетевых методов являются функциональные сети [137]. Они представляют собой языково-алгебраическую систему для описания поведения логико-динамических объектов дискретного типа любой природы, в том числе и деятельности оператора. Функциональные сети являются обобщением аппарата алгоритмических, автоматных, традиционных сетевых методов; они применяются для построения математических моделей, позволяющих получать вероятностные и ресурсные (в том числе и временные) характеристики деятельности оператора. Применение функциональных сетей позволяет перейти от ретроспективных индуктивно-эмпирических методов к более прогностичным дедуктивно-формальным методам исследования, отражающим как специфические свойства отдельных элементов (и человека, и машины), так и их системную результативность и устойчивость функционирования. Еще одной разновидностью сетевых моделей является описание различных управляющих действий человека (более широко — его поступков) с помощью фреймов. Фрейм (от лат. frame — рама, скелет) — это иерархически упорядоченная структура данных, которая является минимально необходимой для задания стереотипных ситуаций или данного класса объектов. В инженерной психологии аппарат фреймов используется для описания и анализа ошибочных действий оператора [78]. Для построения сетевых моделей деятельности оператора может быть использован также математический аппарат сетей Петри [27, 138]. Сеть Петри представляет математическую модель дискретных систем с параллельно функционирующими и асинхронно взаимодействующими компонентами. Предложены немецким ученым К. Петри в начале 60-х гг. Графически сети Петри (рис.8.4) представляют собой двухдольный ориентированный мультиграф с вершинами двух типов: переходами (моделирующими события в дискретной системе) и позициями (моделирующими предусловия выполнения события и постусловия, возникающие после события). Позиции графически обозначаются кружочками, переходы — черточками (рис. 8.4). Направленное ребро может связывать только позицию и переход. Кроме того, задается начальная разметка позиций: каждой из них сопоставляется одно из чисел 0, 1, 2... (число маркеров или фишек). Этим числом моделируется некоторая емкость позиций, количество ресурсов в ней. По отношению к переходам позиции могут быть входными или
Рис. 8.4. Графическое изображение сети Петри.
выходными. Некоторый переход t называется возбужденным или разрешенным (и может сработать), если число фишек его входной позиции р не меньше числа ребер, ведущих из р в t. Срабатывание возбужденного перехода заключается в удалении из каждой его входной позиции р числа фишек, равного числу ребер, ведущих из р в t, и добавлении в каждую его выходную позицию q числа фишек, равного числу ребер, ведущих из t в q. В результате срабатывания перехода получается новая разметка сети Петри. Два возбужденных перехода с общими позициями не должны срабатывать одновременно [166]. С помощью сетей Петри моделируются не временные, а причинно-следственные связи. Они широко применяются для моделирования различных систем. В инженерной психологии их используют для описания, проектирования и исследования деятельности оператора (группы операторов), определения показателей качества деятельности, расчета надежности системы «человек-машина». Например, в работе [138] сети Петри использованы для моделирования групповой деятельности операторов алгоритмических СЧМ. Для этого с каждым переходом сети, соответствующим действиям оператора, связываются соответствующие этому действию математическое ожидание и дисперсия времени, а также вероятность его безошибочного выполнения, а с каждой позицией — вероятность передачи управления, от одного действия к другому. Эти характеристики задаются с учетом сложности и структуры пультов управления операторов, воздействий факторов внешней среды, наличия напряженности в деятельности операторов, вызванной дефицитом времени на выполнение алгоритма. Для определения характеристик деятельности оператора сеть представляется в виде формульной записи. В дальнейшем осуществляется последовательное сокращение этой записи путем применения к каждой из операций формулы соответствующих ей соотношений, которые используются в аналитических методах оценки вероятностных характеристик алгоритмов при элементарных преобразованиях, упрощающих граф, представляющий алгоритм. Собственно моделирование групповой деятельности осуществляется следующим образом. По словесному описанию алгоритма групповой деятельности (инструкции по эксплуатации) строится сеть Петри, отображающая этот алгоритм. Для этого используется система переходов от вершин параллельной граф-схемы алгоритма к фрагментам сети Петри. На основе анализа особенностей групповой деятельности (наличие операций приема и выдачи команд) сделан вывод о целесообразности расширения системы переходов путем введения двух дополнительных вершин типа «прием команды» и «выдача команды», что позволяет упростить процедуру алгоритма построения сети и процедуру его анализа на корректность. В таком виде сеть Петри применяется для априорной оценки групповой деятельности по критериям математического ожидания и дисперсии времени выполнения алгоритма группой, вероятности его своевременного и безошибочного выполнения [138]. На базе структурного подхода строятся также алгоритмические и структурные модели. Алгоритмические модели характеризуются использованием алгоритмического языка, впервые примененного в инженерной психологии Г.М. Зараковским [52]. Модели этого класса в принципе могут использоваться для описания любой целостной деятельности, имеющей дискретный характер. Важнейшими ограничениями для применения этих моделей служат отсутствие в них операций синтеза и нестохастический характер используемых в них алгоритмов. По этой причине алгоритмические модели имеют в основном лишь дискурсивное (от лат. discursis — рассуждение), т. е. формальное, не допускающее расчета применение к сложной целостной деятельности. Однако для отдельных видов деятельности, для которых удается построить алгоритм, введены и нормативные дополнения [цит. по 178]. В этом случае они используются для определения показателей сложности и стереотипности деятельности оператора. Особенно продуктивным применение этих моделей оказывается при использовании нормированных показателей [10]. Структурные модели отображают деятельность оператора с точки зрения ее надежности и эффективности. В определенной мере эти модели представляют собой обобщение алгоритмических для совокупности режимов работы, выполняемых оператором задач, алгоритмов их решения, блоков (составляющих алгоритмы) и конкретных сенсорных, моторных и логических операций. Существенным отличием структурных моделей от алгоритмических является разработка «типовых блоков» с известными (в общем виде) вероятностными и временными характеристиками. Из таких блоков как из «кирпичиков» можно синтезировать структуры сложной деятельности и рассчитывать ее вероятностные и надежностные характеристики. В дальнейшем этот метод трансформировался в функционально-структурную теорию СЧМ, в основе которой лежат рассмотренные ранее функциональные сети [137]. В ряде случаев модели деятельности оператора могут строится на базе математического аппарата теории множеств. Под ней понимается раздел математики, исследующий общее свойство множеств. Множеством называется любое объединение в одно целое некоторых определенных и различных между собой объектов нашего восприятия или мысли [166]. Теоретико-множественные модели в инженерной психологии предложены К-С. Козловым для описания процесса информационного поиска оператором, описания процессов обучения; на их основе разработаны элементы семантической теории информации [7QJ. CJL Борисов использовал теоретико-множественную модель для оценки степени неупорядоченности оперативного поля пультов управления [10]. Дальнейшим развитием теоретико-множественного подхода в инженерной психологии является применение размытых (нечетких) множеств, понятие о которых введено Л. Заде [цит. по 173]. Такой подход основан на том, что ключевые элементы в человеческом мышлении являются классами объектов, в которых переход от принадлежности к одному классу и непринадлежности к нему составляет непрерывный континуум, и. что логика причинно-следственной связи в человеческом мышлении отличается от формальной логики и подчиняется многозначной логике. Класс, который допускает возможность частичного членства, называется размытым, или нечетким, множеством. Такое множество объектов задается с помощью функции принадлежности, принимающей численные значения в диапазоне [0—1] в соответствии со степенью принадлежности объекта к данному множеству. Размытое множество характеризуется функцией принадлежности μа: u ––––––>0,1, описывающей каждый элемент u ϵ U некоторым числом μа (u) из интервала [0—1]. Нечеткое множество наиболее адекватно описывают процессы оперативного мышления оператора, поэтому они являются хорошей моделью для описания процессов принятия решения [27, 195], они находят применение для описания явлений неопределенности, с которой часто сталкиваются при решении различного рода инженерно-психологических задач [184]. Интересна попытка применения Г. Г. Маньшиным аппарата нечетких множеств для проведения инженерно-психологической оценки СЧМ [173].
Поиск по сайту: |
 (8.3)
(8.3)