 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Гарафена – родная мать Осириса. 4 страница
Фото 15. Поверхность Венеры. Съемка «Венера – 14», обработка ИППИ АН СССР и ЦДКС. Меркурий. Но грунта было мало, поэтому не произошло вскипания мантии как у Венеры. Поверхность Меркурия лишь покрылась кратерами и стала похожа на поверхность Луны. Меркурий имеет угловую скорость обращения еще больше, чем Венера, и грунт падал тоже на его левый бок. Но этих остатков грунта было мало и они только замедлили вращение Меркурия до скорости: 1 оборот за 58.65 земных суток. На поверхности Меркурия имеется котловина Колорис (в море Зноя) диаметром 1300 км, по краям которой горы высотой 2 км, долины и гряды простираются за пределы котловины еще на 1300 км. Удар при падении большого астероида образовал волну и создал холмы и долины на противоположной стороне. Этот удар и создал Меркурию самый большой среди планет эксцентриситет, равный 0.206. Этот астероид принес на себе большое количество воды. . Столкновение планет на орбите 420 млн. км от Солнца произошло 2 млрд. лет назад. Цифра 2 млрд. лет назад взята потому, что на Луне (ядре разбитой планеты) нет грунта моложе 2 млрд. лет. Значит ядро освободилось 2 млрд. лет назад, его поверхность в этом возрасте остыла, указав нам дату катастрофы. По моей истории Земли палеомагнетологам предоставляется возможность не по палеомагнитным данным определять положения материков по эпохам, а по положению материков и их палеомагнитным данным определять возраст пород. В истории Земли было 11 катастроф, при которых происходило 11 расширений Земли, значит предварительно необходимо в масштабе: 1 см – 150÷250 км точно изготовить 12 глобусов (1 первичный и 11 после каждой катастрофы) и на них тоже точно (по повреждениям берегов при соприкосновении) разместить материки. Затем при определении в любом месте любого материка направлений палеомагнитных силовых линий интересующей породы, сравнить их с векторной диаграммой магнитных линий этой точки по эпохам, составленной непосредственно с изготовленных глобусов, и узнать точный возраст породы. По векторной диаграмме, например, Африки и Евразии (рис. 12 б, е)), можно подумать, что Африка крутилась примерно на 240°, Евразия перевернулась на 180°. На самом деле меняли свои места полюса Земли, соответственно менялись палеомагнитные данные материков, а все материки смещались со своих мест незначительно (кроме Австралии и Антарктиды). У меня изготовлены только для наглядности 6 глобусов, нет глобусов после катастроф №6, 7, 8, 9, 10, поэтому векторы катастроф №6, 7, 8 положены на вектор катастрофы №5, а векторы катастроф №9 (кувырок) и №10 отражены на современном глобусе. На самом деле это не совсем точно, эти векторы должны быть разделены по точно изготовленным глобусам. На рис. 12 составлены векторные диаграммы магнитных силовых линий по эпохам в произвольно взятых точках материков: а) Северная Америка – точка примерно 114° западной долготы и 38° северной широты, б) Евразия – 75° в.д. и 55° с.ш., в) Южная Америка – 60° з.д., экватор, г) Австралия – 135° в.д. и 25° ю.ш., д) Антарктида – южный полюс. е) Африка – 15° в.д. и 10° с.ш. Обозначения векторов: 0 – докембрий (4600–570 млн. лет назад)
. б . . а . . в г
д е
1 – кембрий (570–510 млн. лет назад) 2 – ордовик (510–439 млн. лет назад) 3 – силур (439–408.5 млн. лет назад) 4 – девон (408.5–362.5 млн. лет назад) 5 – карбон (362.5–290 млн. лет назад) 6 – пермь (290–245 млн. лет назад) 7 – триас (245–208 млн. лет назад) 8 – юра (208–145.6 млн. лет назад) 9 – мел (145.6–65 млн. лет назад) 10 – кайнозой (65 млн. лет назад – 9600 г. до н.э.) 11 – современная эпоха (9600 г. до н.э.- 0) Рис. 12. Векторные диаграммы магнитных силовых линий по эпохам в произвольно взятых точках материков. Расплавленные в «коконах» легкие фракции тонкими вертикальными струйками (плюмы) диаметром до сотни километров поднимаются к поверхности Земли со скоростью 2 м/год. Расположены эти горячие точки в основном в экваториальной зоне Земного шара, т. е. над «коконами» №6, №7, №8, от которых они и исходят. Плюмы, вулканические извержения, гейзеры, «черные курильщики» в океанах, постоянное увеличение радиуса Земли, шевеление литосферных плит – это и есть «дыхания» нагревающихся и расплавляющихся «коконов» в Земле. При каждой катастрофе Земля изменяла свою орбиту в сторону Солнца и это видно на схеме нашей Солнечной системы. Для наглядности изобразим планеты на одной стороне от Солнца, (рис. 13), с расстояниями между ними в масштабе: 1 см – 30 млн. км (см. табл. 2). Получается, что между Меркурием и Венерой -50.2 млн. км, между Землей и Венерой -41.4 млн. км, между Землей и Марсом -78.3 млн. км, между Марсом и разбитой планетой -192 млн. км, между разбитой планетой и Юпитером -358 млн. км, а дальше между планетами разрывы еще больше увеличиваются и притом увеличиваются по нарастающей величине. А вот расстояние между Венерой и Землей меньше, чем между Меркурием и Венерой. Глядя на схему Солнечной системы так и хочется Землю переместить дальше от Солнца на 15 млн. км в положение 3′ для того чтобы расстояния между всеми планетами от Меркурия до Венеры, от Венеры до Земли, от Земли до Марса тоже увеличива- лись бы по нарастающей величине (это предположение полностью подтверждается дальнейшими расчётами). Не вписывающееся положение Земли в Солнечной системе является доказательством ее смещения по причине торможения при каж- Таблица 2.(Интернет).
дой встрече с «кометой», которая обращалась со скоростью меньше, чем Земля. Все выше перечисленные факты дают возможность разработать, начиная с кембрия, процесс расширения Земли от первичного до современного радиуса, дают возможность обнаружить совершенные в этом промежутке времени 2 кувырка Земли, определить даты кувырков, определить новые расположения полюсов после каждого кувырка, определить места полюсов первичной Земли, выявить и определить дату появления спутника Земли – Луны, определить причину единого возраста океанского дна – именно 200 млн. лет, а также дают возможность обосновать следующее Событие. Около 2 млрд. лет назад на орбите 420 млн. км от Солнца, между Марсом и Юпитером произошло Событие – столкнулись две планеты. Потеряв скорость, ком разбитой планеты по плавной снижающейся спирали поплыл к Солнцу. Под действием силы притяжения Солнца, а также сил сопротивления эфира Космоса и отталкивающих сил лучей Солнца за время полета из коры разбитой планеты образовалась вытянутая «комета», которая 570 млн. лет назад стала наползать на орбиту Земли со стороны бывшего Северного полюса в середине Тихого океана, одновременно как и Земля обращаясь вокруг Солнца против часовой стрелки. Впереди летел самый большой астероид. Земля, находясь ближе к Солнцу, имела чуть большую орбитальную скорость, и она обгоняла «комету» на 1 оборот в среднем за 57 млн. лет. Земля 11 раз подлезала под немного продвинувшуюся за это время «комету». Земля притягивала очередную головную часть «кометы», она выпадала на Северный полюс и проваливалась в мантию Земли, увеличивая ее объем. Образовавшиеся континенты расходились радиально, образуя океаны. При каждой катастрофе Земля меняла свой облик: выравнивались или становились круче прежние, образовывались новые складки гор, выдавливались диапиры, изливались траппы по всей Земле. Ядро разбитой планеты стало Луной. Это Событие доказуемо, оно полностью отражено на изготовленных глобусах, полностью подтверждается наличием следов катастроф и движений континентов на современном глобусе, графическими и математическими вычислениями, а также изготовленными макетами, наличием шести порций еще не расплавившегося грунта в мантии Земли, наличием пояса астероидов, периодичностью жизни на Земле (жизнь между катастрофами возрождалась, расцветала и погибала). Метеоры, метеориты, болиды, астероиды, кометы в нашей Солнечной системе, а также кратеры на всех планетах и их спутниках, спутники планет, песок и камни на поверхностях Марса, Земли, Венеры, Меркурия, обратное вращение Венеры, замедленное вращение Меркурия, современное потепление климата и т. д. – последствия одного этого События. Это Событие необходимо осознать, понять и принять. . В аккадской мифологии, как и на шумерской печатке, тоже утверждается, что за Марсом летала водная планета Тиамат и что по очень вытянутой орбите – 1 оборот в 3600 лет – летает еще одна планета Мардук. В другой мифологии планета Мардук называется Нибуру, а на орбите астероидов была планета Фаэтон. Это Событие полностью согласуется с аккадской космогонической поэмой «Энума Элиш» (газета «На грани возможного» №13 (318) 2003 г.). «…явившись извне бог Мардук и богиня Тиамат сошлись лицом к лицу в смертельном поединке». «…Всё тело вдруг её заколыхалось и широко открылся рот», «…он словно створки раковин, его раскрыл». (Тиамат погибла). «Склонившись над верхней частью (кора и верхняя мантия ) он Северному Ветру приказал в края неведомые её доставить ( на Землю). Другую часть (ядро) замыслил он заслоном сделать для небес земных» (Луной). «…из части Тиамат он, как браслет, Великий пояс сотворил» (пояс астероидов). Эти знания аккадцы получили, конечно, от Богов. История Земли: новая трактовка. Обратимся к математическим формулам. Еще в 18 веке астрономы пытались найти планету между Марсом и Юпитером. Уже в то время было известно соотношение: r = 0.3·2n + 0.4, позволяющее приближенно вычислять в астрономических единицах расстояния планет от Солнца. Естественно было, руководствуясь этой формулой, искать планету для которой n = 3 и r = 2.8. Такой планеты в Солнечной системе в настоящее время не существует. Любая планета будет устойчиво летать по своей орбите в вакууме только при условии равенства сил: центробежной и центростремительной (рис. 14). Центробежная сила определяется по формуле: Fц.б. = (Mп·Vn2)/r·gп. Центростремительной силой планеты является сила притяжения планеты Солнцем и определяется по формуле Ньютона: Fц.с. = G·((Mп·MС)/r2); где: G – гравитационная постоянная; Mп – масса планеты; Vn – скорость планеты на орбите; r – расстояние планеты до Солнца; MС – масса Солнца; gп – ускорение силы тяжести на планете. Левые части этих формул равны
Рис. 14. Условие равномерного полета планеты на орбите. Fц.б. = Fц.с., значит и правые части тоже равны: (Mп·Vn2)/r·gп = G·((Mп·MС)/r2). В этом равенстве в левой части центробежная сила, в правой -центростремительная. Рассмотрим, что изменится в этом равенстве, если цельная планета распадется на два куска. Масса каждого куска стала меньше, но в формуле равенства в левой и правой части содержится Mп, значит при уменьшении только массы равенство не нарушается и орбита не изменится. Но при уменьшении скорости левая часть, т. е. центробежная сила уменьшается и правая часть равенства, т. е. центростремительная сила становится больше центробежной. «Комета» и ядро неизбежно полетят к Солнцу с определенной скоростью V2 (рис. 15) и вектор этой скорости будет направлен по радиусу в сторону Солнца. Но «комета» и ядро уже имеют свою орбитальную скорость V1 и вектор ее направлен перпендикулярно радиусу в сторону движения планеты. В точке 1 скорость Vn1 будет суммарной скоростью и она будет рассчитана по теореме Пифагора:
Рис. 15. Полет планеты при потере скорости на орбите.
570 млн. лет назад началась катастрофа №1. Впереди «кометы» летел астероид. Был он формы пирамиды и вершиной вошел в Северный полюс нашей Земли. Представим астероид в виде треугольной пирамиды (рис. 16 справа). Центр тяжести этого сечения будет в точке пересечения медиан, точке 1. Проведем через этот центр тяжести поперечное сечение, тогда центр тяжести левой половины пирамиды будет левее в точке 2, а центр тяжести правой половины будет в точке пересечения ее медиан в точке 3, которая расположена на значительно большем рассто-
Рис. 16. Поворот астероида от полета вершиной к Солнцу к полету вершиной к Земле. янии от точки 1, чем точка 2. А если вся пирамида начнет вращаться, то она будет вращаться вокруг общего центра тяжести, т. е. точки 1. При притяжении Землей пирамиды, как и астероида, к точкам 2 и 3 будут приложены одинаковые силы, но рычаг точки 3 больше, значит астероид, летящий вершиной к Солнцу, неизбежно повернется вершиной к Земле, получив крутящий момент (этот момент и реализовался в мантии Земли, пробив углом В1 отверстие западнее Великобритании). Выполним горизонтальную проекцию большого отверстия в Тихом океане. Проведем на первичном глобусе (фото 5) линии по краям большого отверстия так, чтобы эти линии были бы как линиями пересечения с глобусом плоскости, проходящей параллельно оси Земного шара. Получим точки: А1, D1, В1,С1. Проведем линии А1В1 и B1C1 тоже как линии пересечения плоскости, проходящей через эти точки параллельно оси Земли. Теперь видно, что это отверстие можно представить как треугольник А1В1С1 с примкнувшим к стороне А1В1 еще одним треугольником А1D1В1 и сферы, примкнувшей к стороне В1С1. Приступим к изображению большого отверстия на плоскости. Измерительным циркулем на глобусе (фото 5) измеряем сторону В1С1, наносим ее как горизонтальную линию (рис. 17). Измерительным циркулем измеряем сторону А1С1 и из точки С1 проводим дугу, измеряем сторону А1В1 и из точки В1 проводим дугу. Точка пересечения 2-х дуг есть точка А1. Соединяем эти точки, получим треугольник А1В1С1. Измерим на глобусе сторону В1D1 и из точки В1 проведем дугу, измерим сторону А1D1 и из точки А1 проведем дугу. Точка пересечения двух дуг есть точка D1. Проведем линии В1D1 и А1D1, получаем треугольник В1D1А1. Проведем медианы в треугольнике А1В1С1, получим точку пересечения медиан, точку О, где-то
Рис. 17. Горизонтальная проекция отверстия в районе Тихого океана. здесь и был Северный полюс Земного шара. Точки А1, D1, В1, С1 находятся на глобусе в одной плоскости, поэтому их перенос измерительным циркулем прямо с глобуса достаточно точный. Теперь для более точного измерения и нанесения на плоскость сферической поверхности астероида проведем окружность радиусом 3950 км в масштабе 1 см – 500 км (рис. 18), обозначим на ней вертикальную ось буквами O-O. Для удобства все точки на этой оси в дальнейшем будем обозначать буквами O. На глобусе из середины стороны В1С1 проведем перпендикуляр до пересечения со сферой, обозначим эту точку буквой К1. Измеряем циркулем дугу от точки О до точки К1 и отложим ее от точки О на окружности (рис. 18), получим точку К1 на окружности. Проведем горизонтальную линию от этой точки К1 до пересечения с осью O-O, это и есть горизонтальная проекция дуги ОК1. Измеряем и наносим эту горизонтальную проекцию на рис. 17. Для этого на рис. 17 из середины стороны В1С1 тоже проведем перпендикуляр и на нем из точки O отложим проекцию дуги ОК1 с рис. 18. Теперь проведем дугу через три точки В1, К1, С1. Получилась дуга радиусом 6500 км. Это и есть радиус бывшей планеты.
О Рис. 18. Горизонтальные проекции различных дуг первичного глобуса. Выполним горизонтальную проекцию отверстия в Индийском океане. На первичном глобусе выдвинем Индостан в сторону его современного положения до совмещения их оконечностей (см. рис. 2, фото 6). Индостаном сдвигаются Австралия с Новой Гвинеей и Антарктида. Проведем прямые линии вдоль побережий Индостана и Австралии. Точку пересечения прямых обозначим буквой А2. Точку пересечения прямой с дугой побережья Африки обозначим буквой C2. Проведем из середины наибольшего изгиба дуги, точки К2, перпендикуляр к дуге. Отложим расстояние от точки С2 до перпендикуляра по другую сторону перпендикуляра, обозначим точку В2. Соединим точки В2 и С2. Точку пересечения с перпендикуляром обозначим буквой Е. С помощью кальки перенесем с глобуса дугу на рис. 19, как ее горизонтальную проекцию. Из-за малого размера разница в длинах дуги и ее горизонтальной проекцией мала, ею можно пренебречь. Из середины самого большого изгиба этой дуги, точки К2, проведем линию перпендикулярно этой дуге. Перенесем циркулем с глобуса на рис. 19 точки В2 и С2, соединим эти точки прямой линией. Точку пересечения линии В2С2 с перпендикуляром обозначим буквой Е2. Для наглядности на рис. 19 полуостров Индостан и о. Шри-Ланка изображены такими, какие они есть на современном глобусе. Глядя на первичном глобусе на очертание побережья отверстия от Африки до Индостана довольно отчетливо видны углы, обозначим их буквами В3, В4, В4′, D4 (фото 6). Перенесем проекции этих точек на рис. 19. На глобусе циркулем измерим дугу от точки Е до точки В3, нанесем ее на рис. 18, горизонтальной проекцией этой дуги будет прямая ОВ3, перенесем ее на рис. 19 как продолжение прямой С2В2. На глобусе циркулем измерим дугу ЕВ4, ее горизонтальной проекцией на рис. 18 будет прямая ОВ4. На рис. 19 из точки Е2 проведем дугу радиусом ОВ4. Измерим на глобусе расстояние В3В4, проведем дугу на рис. 19 из точки В3.
Рис. 19. Горизонтальная проекция отверстия в районе Индийского океана. Точка пересечения двух дуг будет горизонтальной проекцией точки В4. Аналогично замером горизонтальных проекций и проведением дуг из точек Е2 и В3 наносим на рис. 19 проекции точек В4′, D4, А2. Соединим точки А2, В2, С2 прямыми линиями, получим треугольник А2В2С2, явно подобный треугольнику А1В1С1 на рис. 17. Подсчитаем коэффициент подобия треугольников А1В1С1 (рис. 17) и А2В2С2 (рис. 19) путем замера и деления соответствующих сторон. Стороны А1С1/А2С2 = 109 мм/52мм = 2.1; Стороны А1В1/А2В2 = 119мм/58мм = 2.1; Стороны В1С1/В2С2 = 130мм/62мм = 2.1. Опираясь на это подобие, начертим на рис. 19 треугольник А2В2D2, подобный треугольнику А1В1D1. Измеряем на рис. 17 сторону В1D1, разделим на коэффициент 2.1, получим: 51/2.1 = 24 мм. На рис. 19 из точки В2 проведем другу радиусом 24 мм. Замерим на рис. 17 сторону А1D1, разделим на коэффициент 2.1, получим 83/2.1 = 40 мм. Из точки А2 проведем на рис. 19 дугу радиусом 40 мм. Точка пересечения двух дуг и будет точкой D2. Соединим прямыми линиями точки А2, D2 и В2, получим треугольник А2D2В2, подобный треугольнику А1D1В1. Вот теперь на рис. 19 видно, что расстояние А2D2 = А2D4, расстояние D2В2 = D4В4 и углы между ними тоже равны, значит дополнительное отверстие А2D2В2В3В4D4 образовалось поворотом сечения вершины астероида А2С2В2D2 вокруг точки А2 по часовой стрелке. Проведем медианы в треугольнике А2В2С2. Наложим сечение вершины астероида на его основание (рис. 19 на рис. 17), совместив точки пересечения их медиан. Видно, что соответствующие стороны основания и сечения параллельны друг другу. Но если центр сечения пирамиды находится точно над центром основания пирамиды и при этом все стороны сечения и основания параллельны друг другу, то это означает, что ось пирамиды перпендикулярна основанию и пирамида является правильной. Все данные дают основание утверждать, что за основу астероида взята правильная треугольная пирамида с прямыми ребрами, с примкнувшими к ней со стороны В1С1 сферой, а со стороны А1В1 еще одной треугольной пирамидой. Можно так же утверждать, что основание астероида тоже является ровной поверхностью, т. к. у него имеются углы с ровными сторонами. На рис. 17 из точки на оси, с которой мы ранее проводили дугу В1К1С1, проведем дугу радиусом 6500 км касательно точки К2. Продлим стороны D2В2 и А2С2 до пересечения с этой дугой, получим углы В5 и С3. Вот этот четырехугольник В5D2А2С3 и должен был быть полным сечением вершины астероида на выходе. Но эта вершина астероида дважды пробила земную кору, прошла путь 7900 км в раскаленной мантии с температурой более 5000 °С и прошла его довольно медленно, поэтому все углы этого четырехугольника оплавились, срезались и округлились. Особенно срезались углы В5 и С3, т. к. они испытывали еще очень сильное давление от двух сторон: А2С2 двигала Австралию с Антарктидой, А2D2 вдавливала полуостров Индостан в материк. Восточная часть Индостана вдавливаясь в материк увлекла за собой ближайшее побережье материка и образовала будущий Бенгальский залив. . Проведем на первичном глобусе (фото 1, 4, 5, зеленый цвет) линию сечения I Земли, как проводили бы экватор. Она проходит по точкам: угол В1, середину повреждения у Великобритании, обозначим ее буквой В1′, и далее эта линия попадает на точку Е. В этой плоскости по этому сечению 1 первичного Земного шара астероид продолжил в мантии Земли вращение, полученное при повороте полета вершиной к Солнцу к полету вершиной к Земле. Проведем на глобусе медианы в треугольнике А2 В2 С2 и обнаруживаем, что сечение проходит мимо центров треугольников А1 В1 С1 и А2 В2 С2, но на одинаковом расстоянии и с противоположных сторон. Земля не получила вращательного движения ни вправо, ни влево от сечения I, значит середина между основанием и сечением вершины астероида совпала с центром Земного шара и центром тяжести всего астероида. Перенесем на рис. 17 проведенное нами на глобусе сечение I, проходящее через отверстие, оставленное основанием астероида (в дальнейшем – сечение 1 основания). Для этого на глобусе (фото 5) замерим циркулем дугу А1Н от угла А1 до точки Н (точки пересечения линии А1С1 с сечением I) и отложим ее на рис. 18. Измерим на рис. 18 ее горизонтальную проекцию и отложим на рис. 17 от угла А1 – точка Н1. На рисунке 17 проведем линию через точки В1 и Н1 – это и будет сечение I основания. Перенесем на рис. 17 и на рис. 19 сечение I, проходящее через отверстие, оставленное вершиной астероида (в дальнейшем – сечение 1 вершины). Для этого циркулем измерим на глобусе (фото 6) расстояние от угла В2 до сечения I и на рис. 19 и на рис. 17 из точки В2 проведем дугу. Замерим на глобусе (фото 6) на стороне А2С2 расстояние от угла С2 до точки пересечения с сечением I и отложим его на рис. 19 и на рис. 17 (точка Н2). Проведем линию через точку Н2 касательно ранее проведенной дуге – это и будет сечение I вершины. Проведем на рис. 19 через точку Е2 перпендикуляр к линии сечения I. Этот перпендикуляр будет осью вращения астероида внутри Земного шара в плоскости сечения I. И эта ось, как и точка Е2, расположены на сечении 1 вершины. Рассмотрим следующие примеры. Возьмем легкий, почти невесомый предмет, например пенопласт, формы невысокого параллелепипеда и поставим его на воду (рис. 20). Астероид в мантии в тот момент, когда вершиной пробил кору изнутри и остановился, был относительно этой коры в невесомом состоянии, т. к. он больше не давил на кору. И если вершину параллелепипеда (рис. 20 а) раскачивать вправо-влево на небольшой угол, то он будет вращаться относительно точки Е2, которая
а б в Рис. 20. Примеры качания предмета на жидкости. расположена на оси вращения. И эта ось, и точка Е2 находятся посередине сечения основания и точку Е2 можно считать неподвижной. Входя в мантию Земли астероид одновременно медленно вращался и передвигался вперед до удара углом В1 возле Великобритании. Скорости этих движений были малы, примерно одинаковы и в точке Е2 направлены в противоположные стороны (рис. 20 б). Кроме того, сечение 1 вершины (где точка Е2) было застопорено со всех сторон: сферой В2К2С2, Индостаном и Австралией. И в этом случае точку Е2 можно считать неподвижной. Есть все основания в этих первичных движениях астероида точку Е2 считать неподвижной. До упора углом В1 возле Великобритании вращение астероида можно рассматривать как результат приложения двух сил инерции к двум концам. Но вот в одном конце (см. рис. 20 в) по причине стопорения угла В1 сила 1 уничтожилась, уткнулась в упор, а сила 2 действует и при малом сопротивлении в точке Е2 астероид может продолжить вращение под действием этой силы 2, только сменится ось вращения, она будет проходить перпендикулярно сечению I в углу В1′. При проведении на рис. 17 сечения I вершины видим, что оно проходит по отношению к линии сечения 1 основания под углом 11°. Значит астероид, до выхода вершины, в мантии Земли крутнулся против часовой стрелки на угол 11°и поэтому сечение вершины на глобусе находится под углом 11° по отношению положения основания. Для определения размера астероида у нас имеются следующие требования: размеры основания и сечения вершины астероида должны быть равны размерам оставленных ими большого и малого отверстий, радиус сферы должен быть равным 6500 км, расстояние от сечения вершины до основания должно быть таким, чтобы при новом радиусе Земли угол В1 астероида едва высунулся бы, а вершина астероида была бы на таком расстоянии от сечения вершины, чтобы его хватило переместить Австралию за о. Калимантан. Выполним проверочные чертежи. . . Наносим две окружности с радиусами 3950 км и 4400 км в масштабе: 1 см – 500 км (рис. 21). Это будет сечение I Земного шара. Нанесем на окружности R = 3950 км точку О1 – проекция на сечение I точки пересечения медиан основания.
Рис. 21. Положение астероида внутри Земли при R = 3950 км и R = 4400 км до и после его поворота на угол 16°. От этой точки с рис. 17 и с глобуса (фото 6) измерительным циркулем наносим на сечение I точки В1′, В5′ (проекцию точки В5 на сечение I), точку Е, точки Z и Н2 (точки пересечения сечения I с сечением вершины). Проведем на рис. 21 через точки Z и Н2 прямую, это будет проекция сечения вершины астероида. Проведем радиус Земли через точку Е. Точка пересечения его с предыдущей прямой будет проекцией точки Е на это сечение, т. е. точкой Е2. Поскольку астероид вращался в плоскости сечения I Земли, то эту точку Е2 мы и принимаем как неподвижную точку, находящуюся на оси поворота астероида. Проведем радиус Земли через точку В1′ до окружности нового Земного шара, обозначим эту точку пересечения как В1″ – это место угла В1 возле Великобритании при новом радиусе Земли с астероидом внутри. И так как повреждение возле Великобритании по длине равно примерно 8 мм, то по макету астероида определяем, что угол В1″ необходимо сделать выступающим примерно на 2 мм (М = 1 см – 500 км). Расстояние между точками Е2 и В1″ дает нам возможность определить расстояние от основания до сечения вершины астероида, для этого рассмотрим астероид по сечению II, проходящему через ось O-O, точки В1 и В2 (рис. 17). Проведем на рис. 17 сечение II и проекцию точки Е2 на сечение II, обозначим эту точку Е2′. Определим расстояние от угла В1 до нее, для этого изобразим на плоскости прямоугольный треугольник В1Е2′Е2. Проведем из одной точки Е2′ вертикальную и горизонтальную линии (рис. 22 а). Вертикальная линия лежит на сечении II и она проходит через точки Е2′, В1. Замерим на рис. 17 расстояние Е2Е2′ и отложим его на горизонтальной линии рис. 22а от точки Е2′. Нам из рис. 21 известно расстояние от точки Е2 до угла В1, оно равно расстоянию Е2В1″, измерим его. На рис. 22 а из точки Е2 проведем дугу радиусом Е2В1. Точка пересечения с вертикальной осью и будет местом точки В1. Соединим прямой точки Е2 и В1. Из полученного прямоугольного треугольника теперь нам известно расстояние В1Е2′. Далее изобразим лежащий на плоскости сечения II четырехугольник Е2′ООВ1. Для этого проведем вертикальную ось О-О (рис. 22 б), отложим перпендикулярно ей с рис. 17 расстояние ОВ1. Из точки В1 проведем дугу радиусом В1Е2′ с рис. 22 а. Замерим на рис. 17 расстояние ОЕ2′ и отложим на рис. 22 б от оси О-О как горизонтальную линию. Точка пересечения этой линии с дугой будет точкой Е2′ лежащей на сечении II и на сечении вершины астероида и ее расстояние до основания на рис. 22 б будет равно расстоянию О-О от основания до сечения вершины астероида в М = 1 см – 500 км. Рассмотрим астероид по сечению III, проходящему через ось О-О, точки К3, К2, А2, А1 (см. рис. 17). Проведем ось астероида (рис. 23), переносим с рис. 17 расстояние ОК3 и ОА1. Переносим с рис. 22 б) расстояние О-О от
Поиск по сайту: |






 Рис. 13. Изображение предполагаемой первичной орбиты Земли в Солнечной системе, М = 1 см – 30 млн. км.
Рис. 13. Изображение предполагаемой первичной орбиты Земли в Солнечной системе, М = 1 см – 30 млн. км.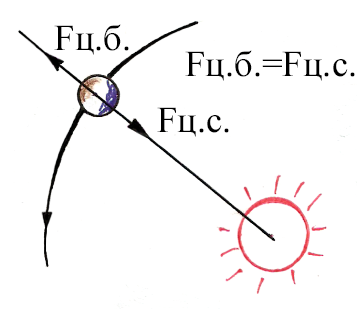

 . И эта скорость будет уже больше, чем скорость V1 и направлена на сближение с Солнцем. В точке 2 линейная скорость будет уже не V1, а Vn1, т. е. больше чем V1 и здесь приобретенная скорость Vn2 будет еще большей, чем Vn1. В последующих точках скорость Vn будет постоянно увеличиваться, и векторы этих скоростей будут направлены на закручивание спирали, т. е. на уменьшение r – расстояния до Солнца. Поэтому и ком бывшей коры, а так же ядро почти параллельным курсом поплыли по плавной снижающейся спиралевидной траектории к Солнцу. Если выше написанное равенство сократить на Mп и r, то получим формулу:
. И эта скорость будет уже больше, чем скорость V1 и направлена на сближение с Солнцем. В точке 2 линейная скорость будет уже не V1, а Vn1, т. е. больше чем V1 и здесь приобретенная скорость Vn2 будет еще большей, чем Vn1. В последующих точках скорость Vn будет постоянно увеличиваться, и векторы этих скоростей будут направлены на закручивание спирали, т. е. на уменьшение r – расстояния до Солнца. Поэтому и ком бывшей коры, а так же ядро почти параллельным курсом поплыли по плавной снижающейся спиралевидной траектории к Солнцу. Если выше написанное равенство сократить на Mп и r, то получим формулу:  . Эта формула необходимой скорости для равномерного полета планеты в вакууме на данной орбите в зависимости от ее расстояния до Солнца.
. Эта формула необходимой скорости для равномерного полета планеты в вакууме на данной орбите в зависимости от ее расстояния до Солнца.




