 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Первый замечательный предел
Второй замечательный предел
или
Полезные пределы 1. 2. 3.
АЗ-2
Вычислить пределы
1. 2. 3. 4. 5. 6. 7.
!!!
8. 9. 10. 11. 12. 13. 14. 15.
ИДЗ-3
Задание 1. Вычислить указанные пределы
Решение типового варианта
1. Воспользуемся первым замечательным пределом (3) предварительно сведя к нему исходное выражение
2. =
3.
4. Сведем исходный предел ко второму замечательному пределу (4)
5. Воспользуемся другой формой записи второго замечательного предела (4’).
Сравнение и эквивалентность бесконечно малых функций
Бесконечно малая функция
Определение. Если
если если если если
Примеры эквивалентных б.м.в (при
Для раскрытия неопределенности вида
АЗ-4
1. Сравнить функции а) в)
2. Доказать, что функцию
3. Найти пределы, используя эквивалентные бесконечно малые функции. а) в) д) ж)
ИДЗ-4
Задание 1. Сравнить бесконечно малые функции
Задание 2. Найти пределы, используя эквивалентные бесконечно малые
Задание 3.* Вычислить пределы функций
Решение типового варианта
Задание 1. Сравнить бесконечно малые функции
Решение. Находим
Задание 2. Найти пределы, используя эквивалентность бесконечно малых
Задание 3. Вычислить предел функции а) Запишем
б) Запишем
Поиск по сайту: |
 (3)
(3) (4)
(4) (4’)
(4’) ;
;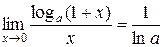 ;
; ;
;  .
. . (5)
. (5) .
. 
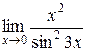 .
. 


 .
. .
. 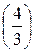
 .
. 




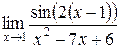 .
. 
 . (0)
. (0) . (0) или
. (0) или 
 .
. 
 .
. 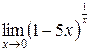 .
. 
 .
. 
 .
.

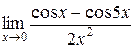














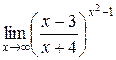
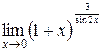
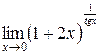






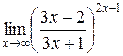



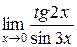
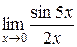


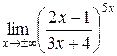






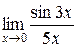


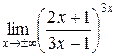









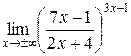


























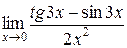






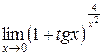







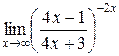

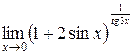






















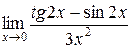

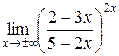




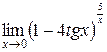



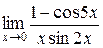
















 .
. =
= 

 =
= 
 .
. ,
, .
.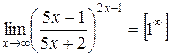 .
.
 .
. .
. .
. (т.е. для любого
(т.е. для любого 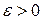 существует
существует  , такое, что при
, такое, что при  справедливо неравенство
справедливо неравенство  ) то
) то  называется бесконечно малой функцией при
называется бесконечно малой функцией при 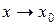 . Для сравнения двух бесконечно малых
. Для сравнения двух бесконечно малых  и
и 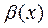 при
при  . (5)
. (5) , то
, то  ;
; , то
, то  , то
, то  , то
, то  )
) ~
~ 
 ~
~  ~
~  ~
~  ~
~ 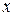
 ~
~  ~
~ 
 ~
~ 
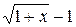 ~
~ 
 можно воспользоваться следующим правилом: если
можно воспользоваться следующим правилом: если  ;
;  при
при 
 и
и 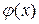 при
при 
 ,
,  ; б)
; б) 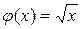 ;
; ; г)
; г) 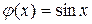 .
. и
и  при
при 
 данные функции одного порядка малости ч.т.д.
данные функции одного порядка малости ч.т.д.
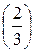 б)
б) 
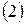

 г)
г) 





















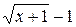


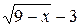





















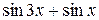


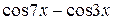












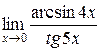


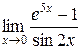



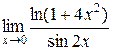


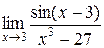





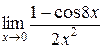









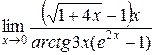



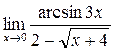

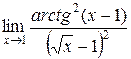


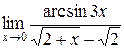




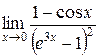


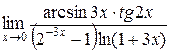






 и
и  при
при 



 как
как  и перейдем к эквивалентной бесконечно малой
и перейдем к эквивалентной бесконечно малой  , получаем
, получаем .
.
 как
как  ~
~ 
 как
как  ~
~  , получим
, получим .
.