 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Математические закономерности эволюции. Понятие бифуркации
Если теория катастроф описывает области устойчивости структур, то развитие этой статической картины во времени дается теорией бифуркаций. Нелинейная система имеет целый спектр решений, и нужно определить, какие из них «ответвляются» от известного решения при изменении параметра. Изменения управляющих параметров способны вызывать катастрофические (большие) скачки переменных состояний, и эти переходы осуществляются почти мгновенно (скачком). Состояние системы, описываемой потенциалом U(xi, са), задается точкой хi в которой потенциал имеет минимум. При изменении внешних условий меняются управляющие параметры с, которые в свою очередь, влияют на изменения U(х, с). Глобальный минимум может стать метастабильным или исчезнуть, а система перейдет из одного локального минимума в другой. Момент перехода определяется свойствами системы и уровнем флуктуаций в ней. Выделяют два принципа: принцип максимального промедления, определяемый существованием устойчивого уровня, и принцип Максвелла, определяющий состояние системы глобальным минимумом. Каждому из принципов соответствует множество точек в пространстве управляющих параметров, в котором происходит переход из одного локального минимума в другой. Последовательность бифуркаций, возникающая с ростом неравновесности в системе, меняется, и процесс пойдет по разным сценариям. Выше описано развитие турбулентности при движении жидкости по трубе в зависимости от числа Re (пропорционального скорости потока). Движение становится неустойчивым и при больших Re характеризуется набором N колебаний с несоизмеримыми частотами Приведем данную Л. П. Кадановым наглядную иллюстрацию перехода к хаосу, которую используют при рассмотрении биологических проблем. Пусть на изолированном острове выводятся летом насекомые численностью с < 1 популяция с ростом / вымирает и исчезает, в области 1 < с < 3 — приближается к значению х = 1 - 1/с, которое получается при подстановке в уравнение вместо Итак, существует диапазон значений параметра с, когда поведение системы упорядочение и периодично; происходит последовательное удвоение периода. Такие решения имеют место для широкого класса систем — химических, электрических, гидродинамических, механических и т.д. В 1978 г. М.Фейгенбаум нашел универсальные законы перехода к хаотическому состоянию при удвоении периода. Если выбрать соседние значения где п = 4,66 для всех систем, то разность между ними убывает с ростом п как аn, где а = 2,5 и тоже является универсальным. Законы Фейгенбаума подтверждены на опытах в совершенно различных по своей природе системах. Иногда их называют (из-за удвоения) законами каскадов Фейгенбаума (рис. 13.5). При с = 3,57 период уже стремится к бесконечности, движение становится апериодическим, поведение системы — хаотическим, происходит перекрытие различных решений. Все расчеты на ЭВМ делаются некорректными, зависящими от случайных процессов в самой вычислительной машине, решения для близких начальных условий оказываются далекими. Сценарии перехода к хаосу могут быть и другими. Исследования сценариев связаны с анализом свойств странных аттракторов, к которым притягиваются точки (состояния системы) в многомерном фазовом пространстве. Введение понятия аттрактора — несомненная заслуга теории катастроф, как и пропаганда знаний об их бифуркациях. Сейчас к этим
терминам привыкли и фонемы речи, к примеру, называют аттракторами звукообразующей динамической системы. Если популяция растет так, что отношение прироста численности к общей численности остается постоянным, то говорят, что закон роста линейный, а рост — экспотенциальный. При приросте 5 % популяция увеличивает свою численность вдвое за 14 лет. Но для роста есть пределы, на что обратил внимание П. Ферхюльст еще в середине XIX в. Он заключил, что прирост должен быть нелинейным. Уравнение Ферхюльста используют и для описания свойств турбулентного потока при приростах около 200%. В этой области происходят колебания, и становится невозможным достижение оптимальной численности. Когда прирост превысит 245 %, происходит такое усложнение поведения систем, что возникает хаос. Это и обнаружил Э.Лоренц для явлений в атмосфере. Свойства аттракторов задаются набором траекторий в пространстве п переменных состояния, зависящих от времени как от параметра. В обычном аттракторе эти траектории простые, среди них есть замкнутые, называемые предельными циклами. В странном аттракторе траектории запутанные, не похожи ни на точки, ни на кривые, ни на поверхности; их представляют многослойными поверхностями. Странность состоит в том, что, попав в область странного аттрактора, точка (выбранное наугад решение) будет «блуждать» там и только через большой промежуток времени приблизится к какой-то его точке. И поведение системы, отвечающее такой точке, будет сильно зависеть от начальных условий. Итак, при медленном изменении параметра наблюдается качественно новое явление затягивания потери устойчиво- сти, описанное в 1973 г. М. А. Шишковой (рис. 13.6). В 1985 г. было показано, что это свойство имеет место во всех системах с медленно меняющимся параметром. После прохождения параметра через бифуркационное значение, соответствующее рождению цикла или мягкому возникновению автоколебаний, система некоторое время остается в окрестности неустойчивого состояния, за которое параметр меняется на конечную величину. После этого система скачком переходит в момент бифуркации в автоколебательный режим (уже ставший жестким). Существование аттракторов с экспоненциально расходящимися фазовыми кривыми на них и устойчивость явлений установлены в начале 60-х гг. XX в. в работах С. Смейла, Д.А.Аносова, Я. Г.Синая. Независимо от этих работ Лоренц в 1963 г. описал наблюдавшийся им в численных экспериментах по моделированию конвекции в атмосфере аттрактор с разбегающимися фазовыми кривыми и указал на связь его с турбулентностью. Перепутывание частот при таком режиме оказывается принципиальным, получается, что частоты определены закона- ми динамики и, следовательно, детерминированы. Поэтому и хаос назван детерминированным. В 1975 г. американские ученые Т. Ли и Дж. Йорк опубликовали статью «Период три дает хаос», где доказали, что при некоторых условиях самопроизвольное появление моды с утроенной частотой возможно только вместе со всем остальным турбулентным спектром. Поэтому хаотический турбулентный режим имеет более сложную структуру, чем упорядоченный ламинарный. Принципиальным в теориях динамического хаоса является признание роли начальных условий, того обстоятельства, что в ходе эволюции система занимает не все точки «фазового пространства». В нем есть определенные места, «цепочки» их концентрации, статистические «аномалии», влияющие на всю микроструктуру. Исследования диалектики случайностей и регулярностей облегчаются возможностями моделирования этих процессов на ЭВМ. Исследования динамического хаоса показывают, что он способен породить не только «унылое равновесие», возникает «вторичная динамика», которую исследуют в синергетике. Итак, в точке бифуркации поведение системы «разветвляется», становится неоднозначным. При достижении третьей бифуркации наступает состояние динамического хаоса, который скрывает внутреннюю упорядоченность. Проблема выяснения условий возникновения порядка из хаоса, по словам известного физика-теоретика Уилера, — задача номер один современной науки.
Поиск по сайту: |
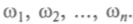 Это квазипериодическое движение называют динамическим хаосом.
Это квазипериодическое движение называют динамическим хаосом.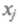 и откладывают яйца. Потомство их появится на следующее лето численностью
и откладывают яйца. Потомство их появится на следующее лето численностью  . Рост популяции насекомых описывается первым членом в правой части уравнения
. Рост популяции насекомых описывается первым членом в правой части уравнения  , а убыль — вторым. При
, а убыль — вторым. При и
и 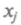 их предельных значений; это область стационарного состояния. В диапазоне 3 < с < 3,4 — две ветви решения, и численность колеблется между ними. Она растет резко от малого значения (откладывается много яиц). Перенаселенность, возникающая на следующий год, вновь резко снижает численность в последующем году, так что период колебаний численности — 2 года. Далее, при 3,4 < с < 3,54 имеем уже 4 ветви, и возникает четырехстадийный цикл колебаний. Так период начинает удваиваться, и далее появляются 8, 16, 32, 64, ... ветвей.
их предельных значений; это область стационарного состояния. В диапазоне 3 < с < 3,4 — две ветви решения, и численность колеблется между ними. Она растет резко от малого значения (откладывается много яиц). Перенаселенность, возникающая на следующий год, вновь резко снижает численность в последующем году, так что период колебаний численности — 2 года. Далее, при 3,4 < с < 3,54 имеем уже 4 ветви, и возникает четырехстадийный цикл колебаний. Так период начинает удваиваться, и далее появляются 8, 16, 32, 64, ... ветвей. цикле,
цикле,
