 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Пороговый характер самоорганизации и представление о теории катастроф
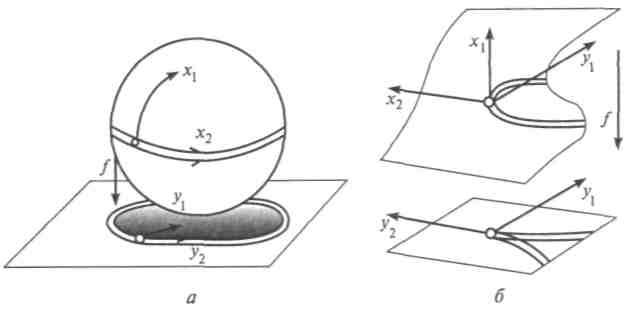
Пороговый характер самоорганизующихся процессов термодинамика связала с неустойчивостью: новая структура есть результат неустойчивости и возникает из флуктуаций. В «допороговом» состоянии флуктуации затухают и макроскопически не проявляются (например, в конвекционном потоке при малых температурах они рассасываются за счет сил вязкого трения). В состоянии выше порога флуктуации уже не рассасываются, а усиливаются, достигают макроскопических значений и выводят систему на устойчивый режим, создают новую структуру, возникающую после неустойчивости. Математически это связано с нелинейностью уравнений, описывающих систему вдали от равновесия. Если линейное уравнение имеет одно стационарное решение, то нелинейное — несколько. Система может принимать любое из этих состояний, и переход из одного в другое стационарное состояние соответствует преодолению порога. Катастрофой называют скачкообразное изменение, которое может возникнуть в ответ на плавное изменение внешних условий. Для систем это означает потерю устойчивости. Область математики, занимающаяся катастрофами, названа теорией катастроф. Она является в некотором роде обобщением исследования функций на экстремум на случай многих переменных и опирается на теорию особенностей гладких отображений. Отображение поверхности на плоскость есть сопоставление каждой точки поверхности с точкой плоскости. Исследования особенностей таких отображений начал в 1955 г. Г. Уитни, ознакомившись с работами Пуанкаре и Ляпунова, а также советских ученых — Андронова, развившего теорию бифуркаций, и Понтрягина, который ввел понятие грубости — структурной устойчивости системы. Важность исследований в направлении, названном К.Зиманом теорией катастроф, оценил французский математик Р. Тома. Он сформировал эту теорию и ее приложения. Сразу появились работы по применению теории катастроф к разным объектам (исследования биения сердца, физическая и геометрическая оптика, лингвистика, геология, эмбриология, гидродинамика, моделирование деятельности мозга и психических расстройств, восстаний в тюрьмах, поведения биржевых игроков и т.д.). Первые публикации по теории катастроф появились в 1970 г. Видный советский математик академик В. И.Ар- нольд так писал о них: «В журналах типа «Ньюс уик» сообщалось о перевороте в математике, сравнимом разве что с изобретением Ньютоном дифференциального и интегрального исчислений. Утверждалось, что новая наука — теория катастроф — для человечества гораздо ценнее, чем математический анализ: в то время как ньютоновская теория позволяет исследовать лишь плавные, непрерывные процессы, теория катастроф дает универсальный метод исследования всех скачкообразных переходов, разрывов, внезапных качественных изменений». Большинство окружающих нас тел ограничено гладкими поверхностями, но видимые контуры тел — это проекции ограничивающих поверхностей на сетчатку глаза. При этом могут возникать некоторые особенности: при проецировании сферы на плоскость в точках экватора образуется складка. На горизонтальной плоскости-проекции выделяется окружность, разделяющая сферу на внутреннюю и внешнюю, при этом точки внутренней сферы имеют по два прообраза (от двух точек сферы), а точки внешней — ни одной, точки окружности — один прообраз. При подходе с внутренней стороны к окружности два прообраза сливаются в один — это и есть особенность складки (рис. 13.4, а). Кроме того, Уитни нашел и другую особенность — сборку (рис. 13.4, б). Представление о ней можно получить, рассматривая устойчивость бутылки из-под молока. Уитни показал, что сборка и складка — устойчивы. Точке экстремума соответствует равенство нулю производной при второй производной, отличной от нуля. В многомерном случае производные от функции U будут браться частные, и они должны быть равны нулю, а смешанные, т.е. вторые производные, отличны от нуля и det
Рис. 13.4. Примеры проецирования поверхностей на плоскость: а — складка проецирования сферы на плоскость; б — сборка проецирования поверхности на плоскость
Такая качественная рельефная картина изменится при наличии вырожденных точек, для которых одно или несколько значений det При пересечении границы областей, являющихся геометрическим местом особенностей, происходят катастрофы состояний системы. Поэтому математики искали эти области и исследовали системы на устойчивость в их окрестностях. Арнольд провел классификацию таких особенностей катастроф и получил удивительное совпадение с классификацией точечных групп, описывающих симметрию молекул, а также с правильными многогранниками в евклидовом пространстве (которыми представлял мир Платон) и простыми группами Ли. Пока причины этих взаимосвязей до конца не выяснены. Приведем для наглядности примеры катастрофы сборки и складки. Для каждого типа катастроф рассматривается поверхность, зависящая от числа переменных и числа управляющих параметров. Обратимся к простейшей катастрофе складки (она похожа на складку на ткани) с одним управляющим параметром. Функция катастрофы задана Cat(t, с) = х3/3 + сх. В области с < 0 все кривые подобны и имеют две критические точки; при с > 0 — кривые также подобны, но критических точек нет; точка с, равная нулю, в пространстве управляющих параметров является сепаратрисой. Катастрофы типа складки появляются в моделях нагруженных арок, триггеров, диссипативных структур, моделях релаксации. Функция катастрофы сборки Cat(x, а, b) = (1/4) х4 + (1/2) ах2 + + bх зависит от одной переменной состояния и двух управляющих параметров. Сепаратриса сборки разделяет плоскость управляющих параметров на две области с одной и тремя критическими точками, ее линии имеют дважды вырожденные точки, а точка пересечения вырождена трижды. Потенциальные функции соответствуют некоторым точкам плоскости управляющих параметров. Модели с функцией сборки встречаются в механике конструк- ций, при описании многих колебательных режимов, в динамике квантовых систем. Теория катастроф позволяет свести огромное многообразие сложных ситуаций к небольшому числу точно изученных схем. Математические образы теории катастроф реализуются в волновых полях. Известны геометрические места точек, в которых происходит фокусировка волнового поля, называемые в оптике каустиками. При пересечении каустик происходит скачкообразное изменение состояния — меняется число лучей, приходящих в данную точку пространства. Для одной-двух переменных и не более пяти управляющих параметров существует семь типов элементарных катастроф. Все семь канонических катастроф имеют в каустиках свои образы. Теория катастроф, широко используемая в метеорологии, аэро- и гидродинамике, оптике, теории кооперативных явлений, квантовой динамике и др., подводит стандартную и эффективную базу под описание качественных изменений в нелинейных уравнениях, описывающих далекие от равновесия системы.
Поиск по сайту: |
 = 0; если потенциальная функция представлена в квадратичной форме, и в случае, например, двух переменных,
= 0; если потенциальная функция представлена в квадратичной форме, и в случае, например, двух переменных, 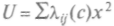 функция будет напоминать рельефную карту: вершины гор и седла связаны хребтами, имеются озерные впадины и седлообразные долины. При диагонализа-ции функции выделяются направления главных осей линий максимального градиента. Если представить рельеф заполненным водой, то она соберется в озера, расположенные в низких частях долин. Минимум, притягивающий воду, получил название аттрактора, причем аттракторы разделяются хребтами, седлами, вершинами на различные бассейны притяжения.
функция будет напоминать рельефную карту: вершины гор и седла связаны хребтами, имеются озерные впадины и седлообразные долины. При диагонализа-ции функции выделяются направления главных осей линий максимального градиента. Если представить рельеф заполненным водой, то она соберется в озера, расположенные в низких частях долин. Минимум, притягивающий воду, получил название аттрактора, причем аттракторы разделяются хребтами, седлами, вершинами на различные бассейны притяжения.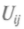 = 0. Это условие получается при некоторых значениях управляющих параметров са. Если при изменении са система проходит через вырожденную точку, меняется вся топология, поэтому и говорят о катастрофе. При приближении к этой точке — границе перехода — критические точки рельефа начинают сближаться, а потом и вовсе сливаются. Множество точек са, отвечающих функции с det
= 0. Это условие получается при некоторых значениях управляющих параметров са. Если при изменении са система проходит через вырожденную точку, меняется вся топология, поэтому и говорят о катастрофе. При приближении к этой точке — границе перехода — критические точки рельефа начинают сближаться, а потом и вовсе сливаются. Множество точек са, отвечающих функции с det 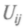 = 0, разбивают пространство управляющих параметров на области с разными рельефами.
= 0, разбивают пространство управляющих параметров на области с разными рельефами.