 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Определение крена сооружений башенного типа
Для определения крена сооружений башенного типа (дымовых труб, эстакад, опор линий электропередач и др.), часто имеющих форму усеченного конуса или пирамиды, производят измерение положения оси сооружения в верхней и нижней точках (рис. 2.62).
Рис. 2.62. Схема определения крена сооружения
Теодолит поочередно устанавливают на двух станциях, расположенных на расстоянии, превышающем высоту сооружения в Расстояние от стоянки теодолита до центра основания сооружения измеряют рулеткой, нитяным или светодальномером. При невозможности непосредственного измерения линии, ее определяют как неприступное расстояние (см. п. 2.3.3.2). Высоту сооружения определяют с помощью тригонометрического нивелирования (см. п. 2.3.3.2). На каждой станции при каком-то положении вертикального круга (например, при КЛ) берут четыре отсчета по горизонтальному кругу теодолита: два – по верхним краям сооружения и два – по нижним. Полусуммы отсчетов позволяют определить положение оси вверху и внизу. Если сооружение в рассматриваемой плоскости крена не имеет, то полусуммы отсчетов вверху и внизу совпадут. Несовпадение полусумм свидетельствует о наличии крена сооружения. Разность полусумм дает проекцию углового крена вертикальной оси сооружения на горизонтальную плоскость Значение линейного смещения верхней точки оси сооружения относительно нижней точки, измеренная со станции I, определяется по формуле:
где dI – горизонтальное расстояние от станции I до центра основания сооружения. Значение линейного смещения в перпендикулярной плоскости визирования определяется аналогичным образом со станции II:
Полная величина линейного горизонтального смещения равна 2.3.3.2. Решение некоторых инженерных задач, Определение неприступного расстояния. Неприступное расстояние – это расстояние до объекта, находящегося в поле зрения наблюдателя, которое не может быть измерено непосредственно. Это чаще всего связано с наличием на местности каких-то препятствий (забор, водоем и т. п.). В таком случае прибегают к косвенному способу измерений, когда измеряются какие-то дополнительные величины (линейные, угловые или физические), а искомое расстояние вычисляется с их помощью.
Рис. 2.63. Схема определения неприступного расстояния
Неприступное расстояние определяют, как правило, из системы двух треугольников, построенных на основе измеренных базисов. Базисы разбивают на слабопересеченной местности, длина их должна быть не менее половины измеряемого расстояния. Базисные расстояния измеряют лентой или рулеткой с точностью 1/2000–1/3000, углы – теодолитом полным приемом. Схема определения неприступного расстояния показана на рис. 2.63. Из решения треугольников ABC и ADC определяют неприступное расстояние по формулам:
Относительная погрешность двух вычисленных значений неприступного расстояния не должна превышать 1/1000AC. При этом условии неприступное расстояние принимается равным среднему арифметическому двух вычисленных. Например,
Среднее значение неприступного расстояния
Определение высоты сооружения. Для определения высоты сооружения башенного типа на некотором расстоянии от него устанавливают теодолит и измеряют вертикальные углы
где d – горизонтальное проложение линии, которое может быть измерено лентой, рулеткой или дальномером. При невозможности непосредственного измерения линии ее вычисляют как неприступное расстояние, разбив предварительно базисы. Для контроля проводят такие же измерения и вычисления с другой точки (см. рис. 2.63). Например,
Аналогично обрабатывают результаты измерений со станции на точке B.
Поиск по сайту: |

 . После выполнения аналогичной процедуры при другом положении вертикального круга (КП) получают
. После выполнения аналогичной процедуры при другом положении вертикального круга (КП) получают  . При получении допустимого расхождения между этими двумя значениями, которое обычно ограничивается величиной 2t, где t – точность отсчетного устройства теодолита, вычисляют среднее значение
. При получении допустимого расхождения между этими двумя значениями, которое обычно ограничивается величиной 2t, где t – точность отсчетного устройства теодолита, вычисляют среднее значение  .
. , (2.36)
, (2.36) . (2.37)
. (2.37) , а угловой крен вычисляется по формуле (2.35).
, а угловой крен вычисляется по формуле (2.35).
 ; (2.38)
; (2.38) . (2.39)
. (2.39)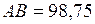 м,
м,  м,
м,  ,
,  ,
,  ,
,  . Вычисляем неприступное расстояние
. Вычисляем неприступное расстояние м;
м; м.
м. м.
м. и
и  при двух положениях вертикального круга: КЛ и КП (см. рис. 2.63). Тогда высота сооружения равна:
при двух положениях вертикального круга: КЛ и КП (см. рис. 2.63). Тогда высота сооружения равна: , (2.40)
, (2.40) м,
м,  ,
,  .
. м;
м;  м;
м;  м.
м.