 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Способ полярных координат
Способ полярных координат широко используется для выноса точек в натуру при любых формах разбивочных сетей. На ближайшем к сооружению пункте А (рис. 2.22) устанавливают теодолит, от стороны разбивочной сети строят угол
Способ линейной засечки Способ линейной засечки может быть использован, если расстояние от выносимой точки до пунктов разбивочной сети меньше длины мерного прибора. Положение на местности искомой точки Р получают на пересечении двух дуг, радиусы которых равны проектным расстояниям
Рис. 2.23. Построение точки способом линейной засечки
Точность построения точки Р способом линейной засечки может быть предвычислена по формуле
где
Способ проектного полигона
Способ проектного полигона применяют для выноса в натуру нескольких точек, если расстояния между ними не слишком велики. Из решения обратной геодезической задачи находят длины сторон
Рис. 2.24. Построение точек способом проектного полигона
В конечной точке D¢измеряют величину и магнитный азимут направления линейной невязки DD¢. Если невязка не превышает допустимого значения, то точки В¢, С¢и D¢спомощью линейки перемещают в проектное положение по направлению магнитного азимута DD¢ на расстояния, пропорциональные их удалению от начала хода:
Полученные точки закрепляют.
Поиск по сайту: |
и фиксируют направление на местности точкой 
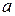. Затем в полученном направлении откладывают расстояние d и закрепляют положение разбиваемой точки Р. Значения горизонтального угла и расстояния находят из решения обратной геодезической задачи.
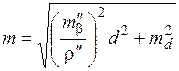, (2.28)
где 
и 
–средние квадратические погрешности построения угла и расстояния соответственно.
и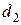 
до пунктов А и В разбивочной сети (рис. 2.23).
, (2.29)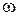
– угол засечки; 
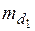и 
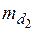– средние квадратические погрешности отложения расстояни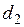й.
, 
и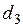 
и внутренние углы проектного полигона 
, 
, 
и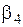 
(рис. 2.24). Затем, откладывая углы и расстояния, последовательно находят положения точек В¢, C¢и D¢, которые вследствие погрешностей построения углов и расстояний не совпадут с проектными точками.
, 
.