 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Порядок составления дифференциальных уравнений движения САУ
Прежде чем составлять дифференциальное уравнение системы, необходимо разобраться в принципе ее действия и на основании этого -составить функциональную структурную схему системы, т. е. представить систему в виде взаимно связанных элементов, каждый из которых выполняет свою функцию. - для каждого элемента системы следует составить дифференциальное уравнение динамики, связывающее выходную величину со входными*. -Количество таких уравнений должно равняться числу зависимых переменных, что является необходимым (но недостаточным) признаком правильности составления уравнений. -исключив промежуточные переменные (из-за связи между элементами системы выходная величина одного из них является входной величиной другого или нескольких других), можно, наконец, получить одно дифференциальное уравнение, в котором независимыми переменными являются внешние воздействия и время, а зависимой переменной — управляемая величина или ошибка системы. Уравнения динамики принято записывать таким образом, чтобы выходная величина и все её производные находились в левой части уравнения, а входные величины и их производные – в правой части уравнения. Уравнение динамики считается написанным в нормальной форме, если выходная величина элемента входит в преобразованное уравнение с коэффициентом, равным единице. Зная передаточные функции элементов САУ, можно получить передаточную функцию, а по ней частотные и временные характеристики всей системы.
Понятие устойчивости линейных непрерывных САУ. Критерии Устойчивости. Любая САУ характеризуется переходным процессом, который возникает в ней при нарушении состояния равновесия вследствие какого-либо воздействия. Переходный процесс х(t) зависит как от свойств системы, так и от вида возмущающего воздействия. В переходном процессе различают две составляющие:
Основной динамической характеристикой САУ является ее устойчивость. Под устойчивостью понимается свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, которое вывело ее из этого состояния. Физическую трактовку понятия устойчивости можно пояснить следующим примером. Если шар помещен в верхнюю точку возвышенности (рис. 2.17, я), то система неустойчива, поскольку при малейшем отклонении шара от начального положения он скатится по склону поверхности и не возвратится в исходное положение. Если же шар помещен во впадине (рис 2.17,6), то система устойчива: после отклонения шар обязательно возвратится к первоначальному положению. В обеих ситуациях устойчивость и неустойчивость системы не зависят от величины начальных отклонений шара. Однако возможны случаи, когда система при малых отклонениях будет устойчива, а при больших—неустойчива, например, если шар находится во впадине, а впадина расположена на вершине выпуклой поверхности (рис. 2.17,0). Принято считать, что такая систем; устойчива в малом и неустойчива в большом, поскольку устойчивость связана с величиной начального отклонения.
Если свободная составляющая не стремится ни к нулю, ни к бесконечности, то система находится на границе устойчивости. Для определения устойчивости линейной непрерывной САУ можно применять следующее общее условие устойчивости (Правило Ляпунова): Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательны.
непосредственное применение, заключается в необходимости поиска корней характеристического полинома. Существуют различные критерии (условия), позволяющие судить о знаках корней характеристического уравнения по его коэффициентам, не решая это уравнение. Различают две группы критериев устойчивости: алгебраические (Рауса и Гурвица), основанные на анализе коэффициентов характеристического уравнения, и частотные (Михайлова), основанные на анализе частотных характеристик.
Поиск по сайту: |
 первая из них выражает вынужденные движения, определяемые возмущающим воздействием и свойствами системы; вторая — свободные движения системы, определяемые начальными условиями и свойствами самой системы.
первая из них выражает вынужденные движения, определяемые возмущающим воздействием и свойствами системы; вторая — свободные движения системы, определяемые начальными условиями и свойствами самой системы. Система автоматического управления будет устойчива, если в переходном процессе свободная составляющая с течением времени стремится к нулю, т. е. если
Система автоматического управления будет устойчива, если в переходном процессе свободная составляющая с течением времени стремится к нулю, т. е. если  . Если стремится к бесконечности, то САУ считается неустойчивой.
. Если стремится к бесконечности, то САУ считается неустойчивой.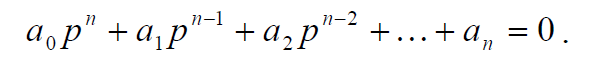 Основной недостаток правила Ляпунова, затрудняющий его
Основной недостаток правила Ляпунова, затрудняющий его