 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Дифференциальные уравнения теплопроводности в твердом теле
Дифференциальное уравнение теплопроводности Фурье для изотропного твердого тела в декартовой системе координат (установлен Ж.Б. Фурье в 1822 г.) имеет вид:
Если температурное поле стационарное – имеем дифференциальное уравнение Пуассона:
Дифференциальные уравнения Фурье, Пуассона и Лапласа могут быть Теплопроводность через однослойную и многослойную плоскую стенки при граничных условиях первого рода
Согласно закону Фурье, тепловой поток проходящий через стенку, прямо пропорционален поверхности, разности температур t1 и t2 и обратно пропорционален толщине δ. Тогда
Отношение
Схема передачи теплоты теплопроводностью через плоскую однослойную стенку Передача теплоты может осуществляться через многослойную плоскую стенку. Примером может служить теплоизоляционное ограждение стационарных холодильных камер. Рассмотрим определение теплового потока теплопроводностью через многослойную стенку (рис. 4.4).
Схема передачи теплоты теплопроводностью через плоскую многослойную стенку В этом случае термическое сопротивление многослойной стенки определится как сумма термических сопротивлений всех слоев: Rλ =δ/λ1+δ2/λ2+…+δn/λn Плотность теплового потока равна
Распределение температур в пределах каждого слоя – линейное, однако в различных слоях угол наклона температурной прямой отличается: более резко изменяется температура в том материале, который является лучшим теплоизолятором или имеет меньшее значение λ.
Поиск по сайту: |
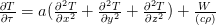
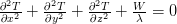



 называется тепловой проводимостью стенки, а обратная величина δ/λ (м2К/Вт) - термическим сопротивлением (Rλ) теплопроводности.
называется тепловой проводимостью стенки, а обратная величина δ/λ (м2К/Вт) - термическим сопротивлением (Rλ) теплопроводности.

