 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Діаграма граничних напружень. Коефіцієнт запасу втомної міцності
Зазвичай, розрахунки на міцність деталей, що працюють при змінних напруженнях, виконують як перевірочні. При такому розрахунку визначають фактичні коефіцієнти запасу міцності
Величина необхідного коефіцієнта запасу міцності Коефіцієнт запасу міцності Найпростіше визначити
При асиметричному циклі ситуація ускладнюється, тут граничний стан характеризується двома величинами: середнім напруженням і відповідною граничною амплітудою. Для визначення коефіцієнтів запасу використовують діаграму граничних напружень (діаграму Хея). Її будують в координатах Зазвичай діаграму граничних напружень схематизують. Видаляють ту область де максимальні напруження
Початкову ділянку діаграми замінюють прямою, яка проходить через дві точки, що відповідають симетричному граничному циклу
 - коефіцієнт чутливості до асиметрії циклу. - коефіцієнт чутливості до асиметрії циклу.
Ламана лінія Нехай задано робочий режим деталі, що характеризується змінним напруженням
і змінним напруженням тч.
Граничні значення постійної і змінної складових напруження тч.
Аналітичні вирази для коефіцієнтів запасу міцності отримаємо при спільному розв’язуванні рівнянь прямих ділянок
Із двох значень При асиметричних циклах кручення аналогічним чином отримаємо
При дії згину із крученням користуються загальноприйнятою на даний час емпіричною залежністю Гафа-Поларда
12 РОЗРАХУНКИ ПРИ УДАРНИХ
Ударом називають навантаження, що передається тілу протягом малого проміжку часу і викликає в ньому значні прискорення, а отже і значні сили інерції. За характером прикладання сили до стержня розрізняють поздовжній, поперечний та крутний удари.
Технічна теорія удару
Визначення прискорень частинок матеріалу при ударі досить проблематичне. Тому для розв’язання задач зазвичай використовують закон збереження енергії. При цьому будують спрощену розрахункову модель системи, що базується на кількох припущеннях, які в більшості випадків забезпечують достатній для інженерних розрахунків рівень точності. 1. Напруження, що виникають в системі при ударі, не перевищують границю пропорційності матеріалу, тобто завжди можна використовувати закон Гука. 2. Удар будемо вважати ідеально непружним (без відскакування). Тобто падаюча маса після удару наче прилипає до тіла, що зазнає удару, після чого вони продовжують рухатися разом. 3. Місцеві деформації, що виникають в місці контакту тіл не враховуємо. 4. Розглядаємо випадки, коли маса пружного тіла, що зазнає удару, мала порівняно з масою тіла, що удару завдає. Тому пружну систему вважаємо безмасовою. Разом з цим нехтуємо явищем розповсюдження хвиль деформацій. 5. Вважаємо, що кінетична енергія, падаючого тіла повністю перетворюється у потенціальну енергію пружної деформації тіла, яке сприймає удар. 6. Закон розподілу напружень і деформацій по об’єму тіла, яке зазнає удару, залишається таким самим як і при статичній дії сил. На основі цих припущень визначимо переміщення і напруження, що виникають в стержнях при ударі. Зазначимо, що в рамках технічної теорії удару можна врахувати вплив маси пружної системи. Це підвищує точність розрахунків.
Поздовжній удар
Нехай на стержень довжиною
а потенціальна енергія пружної деформації стержня
Використовуючи вираз закону Гука
Врахуємо, що абсолютне видовження стержня при статичному прикладанні вантажу (рис. 12.1,б)
тоді розділивши ліву і праву частини рівняння (12.4) на жорсткість стержня
Розв’язавши його відносно
В останній формулі слід остаточно прийняти знак плюс, оскільки знак мінус не відповідає фізичному змісту задачі (очевидно, що Позначивши динамічний коефіцієнт при поздовжньому ударі як
отримаємо
а враховуючи лінійний зв’язок між напруженнями і деформаціями
де Вираз для динамічного коефіцієнта (12.6) можна записати в іншому вигляді, якщо скористатися залежністю між висотою
Коли навантаження прикладається раптово ( Якщо вантаж падає з великої висоти
Поперечний удар
 вільно падає вантаж вільно падає вантаж  (рис. 12.2,а). Розв’язуючи задачу так само, як і при поздовжньому уда-рі, прийдемо до рівняння (рис. 12.2,а). Розв’язуючи задачу так само, як і при поздовжньому уда-рі, прийдемо до рівняння
Вираз (12.11) однаковий для довільних умов на краях балки. Можуть змінюватися лише абсолютні значення Розв’язавши рівняння (12.11) відносно
де
- динамічний коефіцієнт при поперечному ударі.
Крутний удар
Нехай на вал
де Розглядаючи лише кручення вала та вважаючи, що кривошип абсолютно жорсткий, маємо
де Часто ударне кручення спричинюється не падінням вантажів, а силами інерції мас, що обертаються з великим прискоренням при миттєвому гальмуванні. Наприклад, при гальмуванні швидко-обертових валів, що несуть маховики (рис. 12.4).
де Потенціальна енергія деформації кручення вала
де Тоді закон збереження енергії набирає вигляду
Звідки визначимо крутний момент, що діє в перерізах вала
Далі за відомими формулами, можемо визначити дотичні напруження та кути закручування перерізів вала.
Поиск по сайту: |
 для одного чи декількох потенційно небезпечних перерізів деталі. Умова міцності має вигляд
для одного чи декількох потенційно небезпечних перерізів деталі. Умова міцності має вигляд .
.
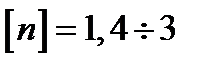 залежить від ряду обставин (призначення деталі, умови роботи, точності визначення діючих навантажень і т.п.) і вибирається згідно із прийнятими нормами чи існуючим досвідом експлуатації деталі.
залежить від ряду обставин (призначення деталі, умови роботи, точності визначення діючих навантажень і т.п.) і вибирається згідно із прийнятими нормами чи існуючим досвідом експлуатації деталі. , до номінального значення максимального напруження, що виникає в небезпечній точці деталі. Номінальним є значення напруження, що визначене методами опору матеріалів (без врахування концентрації і т.п.).
, до номінального значення максимального напруження, що виникає в небезпечній точці деталі. Номінальним є значення напруження, що визначене методами опору матеріалів (без врахування концентрації і т.п.). ;
;
 .
.
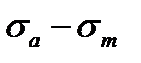 (рис. 11.5). Всередині області, що обмежена координатними осями
(рис. 11.5). Всередині області, що обмежена координатними осями  ,
,  і кривою граничних напружень не відбувається руйнування при необмеженій кількості циклів навантаження.
і кривою граничних напружень не відбувається руйнування при необмеженій кількості циклів навантаження. перевищують границю текучості матеріалу. Для цього через точку
перевищують границю текучості матеріалу. Для цього через точку  , що відповідає границі текучості, під кутом
, що відповідає границі текучості, під кутом  проводять пряму (рис. 11.5), рівняння якої
проводять пряму (рис. 11.5), рівняння якої .
.
 і граничному пульсуючому циклу
і граничному пульсуючому циклу  . Рівняння цієї прямої має вигляд
. Рівняння цієї прямої має вигляд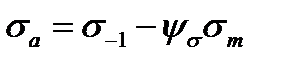 ,
,
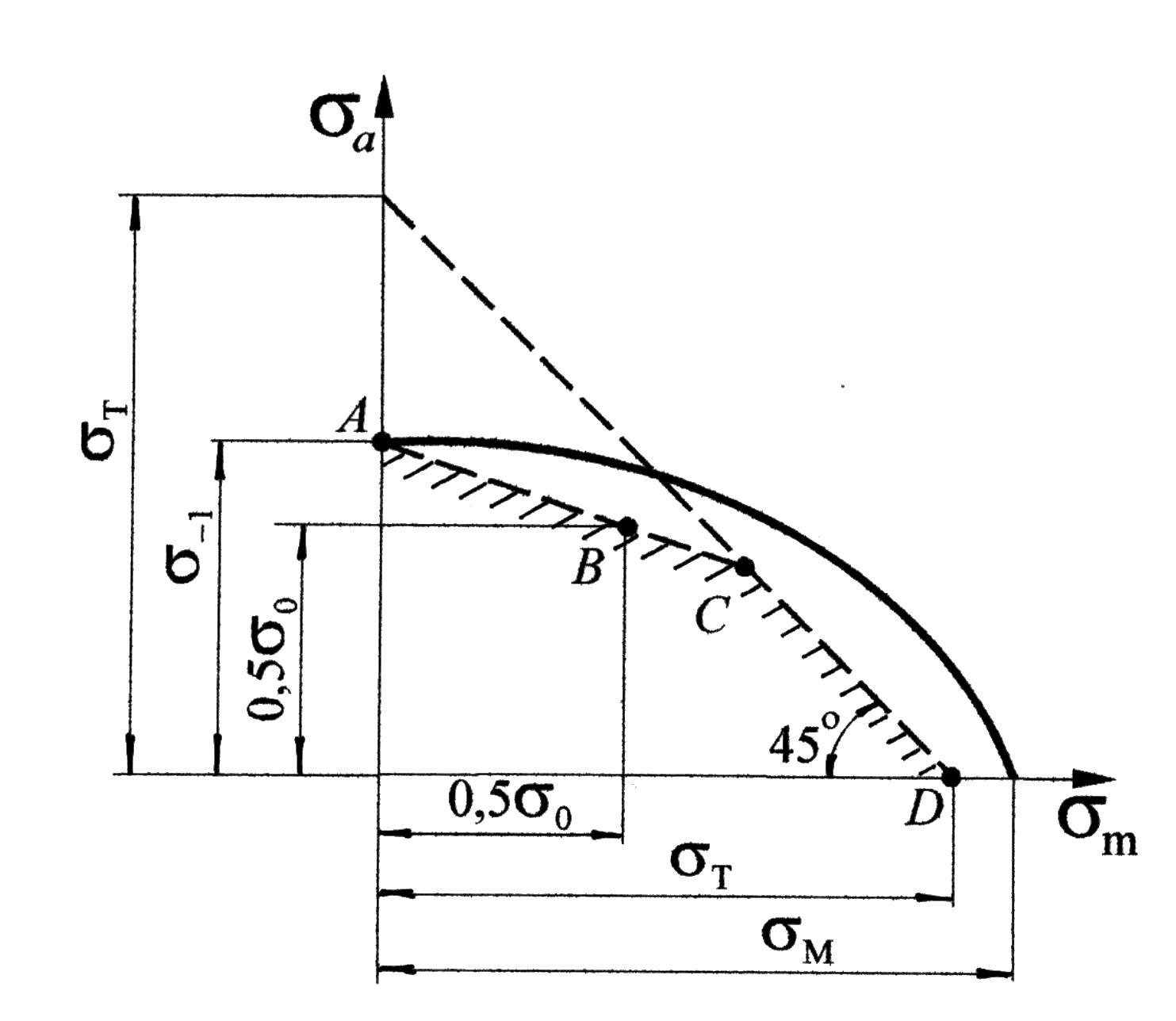 Рисунок 11.5
Рисунок 11.5
 Рисунок 11.6
Рисунок 11.6
 (рис. 11.5) обмежує область безпечної роботи конструкції: на ділянці
(рис. 11.5) обмежує область безпечної роботи конструкції: на ділянці  - рівнянням (11.15); на ділянці
- рівнянням (11.15); на ділянці 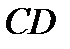 - рівнянням (11.16).
- рівнянням (11.16).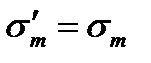
 (рис. 11.6)
(рис. 11.6) .
.
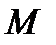 (рис. 11.6)
(рис. 11.6) ,
, 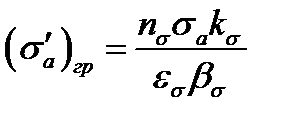 .
.
 і
і  із врахуванням виразів (11.17)
із врахуванням виразів (11.17) 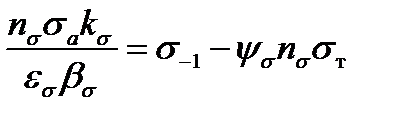 ,
,  , звідки
, звідки ,
, 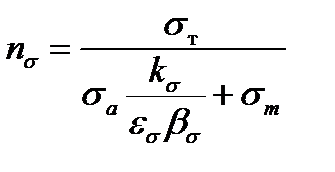 .
.
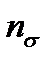 , що визначаються виразами (11.18), шуканим є менше значення.
, що визначаються виразами (11.18), шуканим є менше значення. ,
, 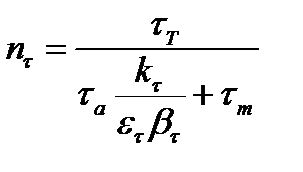 .
.
 .
.
 з висоти
з висоти  , позначимо
, позначимо  . Оскільки швидкість падаючого вантажу в кінці удару дорівнюватиме нулю, то зміна кінетичної енергії дорівнюватиме роботі сили
. Оскільки швидкість падаючого вантажу в кінці удару дорівнюватиме нулю, то зміна кінетичної енергії дорівнюватиме роботі сили  ,
,
 .
.
 Рисунок 12.1
Рисунок 12.1
 .
.
 , визначимо
, визначимо  . (12.4)
. (12.4) ,
,
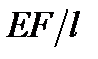 прийдемо до зведеного квадратного рівняння
прийдемо до зведеного квадратного рівняння .
.
 , матимемо
, матимемо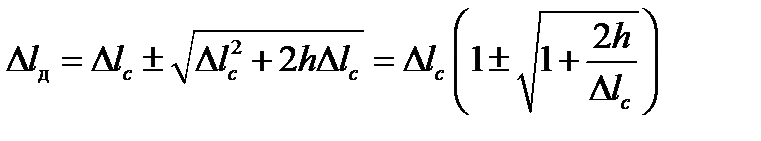 .
.
 ).
). ,
,
 ,
,
 ,
,
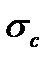 - напруження, що виникає при статичному прикладанні навантаження.
- напруження, що виникає при статичному прикладанні навантаження. у момент зіткнення. Знаючи, що
у момент зіткнення. Знаючи, що  , звідки
, звідки  , матимемо
, матимемо .
.
 ,
,  ), то
), то 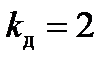 , а
, а  ;
;  .
. , то вираз для динамічного коефіцієнта спрощується:
, то вираз для динамічного коефіцієнта спрощується: .
.
 Рисунок 12.2
Рисунок 12.2
 .
.
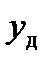 і
і  .
. ,
,

 Рисунок 12.3
Рисунок 12.3
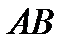 через кривошип
через кривошип  передається ударне навантаження (рис. 12.3). У цьому випадку дотичні напруження в точках вала визначають за формулою
передається ударне навантаження (рис. 12.3). У цьому випадку дотичні напруження в точках вала визначають за формулою , (12.14)
, (12.14) - динамічний коефіцієнт;
- динамічний коефіцієнт;  - переміщення точки співудару в напрямі удару під дією статично прикладеної сили
- переміщення точки співудару в напрямі удару під дією статично прикладеної сили  ,
,
 - кут закручування торця вала під дією крутного моменту
- кут закручування торця вала під дією крутного моменту  .
. Рисунок 12.4
Рисунок 12.4
 ,
,
 ‑ полярний момент інерції маси маховика, що обертається з кутовою швидкістю
‑ полярний момент інерції маси маховика, що обертається з кутовою швидкістю  .
. ,
,
 - кут закручування вала.
- кут закручування вала. ,
,
 .
.