 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Рівняння трьох моментів
Статично невизначену балку, що має більш ніж дві опори називають нерозрізною.
При такій основній системі невідомими у рівняннях переміщень будуть згинні моменти, що виникають над опорами нерозрізної балки при її навантаженні. Припустимо, що ці опорні моменти додатні. Прикладемо їх разом із заданим навантаженням до простих балок основної системи і отримаємо еквівалентну систему (рис. 8.4,б). Під дією такого навантаження прості балки еквівалентної системи деформуються і, зокрема, їх опорні перерізи повертаються один відносно одного на певний кут, що позначений на Рівняння переміщень випливає з умови, що реальна нерозрізна балка проходить суцільно над всіма опорами і тому опорні перерізи однопрольотних балок еквівалентної системи не можуть повертатися один відносно одного, тобто
Використовуючи принцип незалежності дії сил
де Коефіцієнти рівняння (8.8) визначимо за способом Верещагіна (рис. 8.5):
Вільний член рів-няння (8.8)
Після підстановки значень коефіцієнтів і вільного члена у рівняння (8.8) отримаємо
Одержане рівняння переміщень для нерозрізної балки називають рівнянням трьох моментів. Таких рівнянь треба скласти стільки, скільки балка має зайвих опор. Якщо момент інерції нерозрізної балки змінюється від прольота до прольота, то рівняння (8.10) набуде вигляду
де
Кути повороту опорних перерізів Іноді праву частину рівняння (8.10) зручно представити в іншому вигляді
де Після визначення опорних моментів
СКЛАДНИЙ ОПІР Загальні поняття
Складний опір виникає у випадку, коли в поперечних перерізах стержня одночасно діє не менше ніж два внутрішні силові фактори (виключенням є прямий поперечний згин, що відносять до простого опору стержня, оскільки в практичних розрахунках впливом поперечної сили зазвичай нехтують).
 і згинні моменти і згинні моменти  , ,  викликають в поперечному перерізі нормальні напруження. Поперечні сили викликають в поперечному перерізі нормальні напруження. Поперечні сили  , ,  , і крутний момент , і крутний момент  викликають дотичні напруження. викликають дотичні напруження.
Всі види складного опору можна розділити на три групи: 1. Складний опір, при якому в довільній точці перерізу можуть виникати лише нормальні напруження
2. Складний опір, при якому в довільній точці перерізу виникають лише дотичні напруження
3. Складний опір, при якому в точках перерізу одночасно виникають нормальні і дотичні напруження (плоский напружений стан), що можуть бути враховані в розрахунках шляхом застосування однієї із теорій міцності.
Косий згин
Розрізняють плоский косий згин, коли всі зовнішні сили лежать в одній площині, а пружна лінія балки – плоска крива і просторовий згин, коли зовнішні сили діють в різних площинах (площини згинних моментів в різних поперечних перерізах орієнтовані по різному), а пружна лінія балки – просторова крива. Розглянемо плоский косий згин консольної балки (рис. 9.3). Розкладемо зовнішню силу
 і і  , що діють в головних площинах інерції балки. Сумуючи напруження і деформації, що відповідають поперечним згинам, отримаємо розв’язок задачі косого згину. , що діють в головних площинах інерції балки. Сумуючи напруження і деформації, що відповідають поперечним згинам, отримаємо розв’язок задачі косого згину.
Згинні моменти в перерізі з абсцисою
 - повний згинний момент; - повний згинний момент;  - кут між віссю - кут між віссю  і площиною дії повного моменту (рис. 9.4,б). і площиною дії повного моменту (рис. 9.4,б).
Розділивши перший вираз (9.1) на другий, одержимо
Щоб знайти положення площини дії повного згинного моменту необхідно вісь знаку (на рис. 9.4 це будуть I і ІІІ квадранти). Нормальні напруження в довільній точці поперечного перерізу балки визначаємо за формулою
У формулу (9.3) згинні моменти Рівняння нейтральної лінії отримаємо, розглядаючи її як геометричне місце точок перерізу, в яких нормальні напруження дорівнюють нулю
звідси
Це рівняння прямої з кутовим коефіцієнтом
Отже, щоб знайти положення нейтральної осі потрібно вісь З формули (9.5) бачимо, що в загальному випадку кут Формулу (9.3), враховуючи (9.1) приведемо до іншого вигляду
де У випадку, коли переріз має дві осі симетрії (прямокутник, двотавр), напруження в найбільш віддалених від нейтральної осі точках однакові за величиною і відрізняються лише знаком. Умова міцності для пластичного матеріалу має вигляд
де Для виконання проектного розрахунку рівняння (9.7) зручно представити у вигляді
де
Якщо Повернемося до прикладу (рис. 9.3) та знайдемо прогин вільного торця балки: - прогин від дії сили
- прогин від дії сили
- повний прогин (рис. 9.6)
 і віссю і віссю 
 спрямовано перпендикулярно до нейтральної осі. спрямовано перпендикулярно до нейтральної осі.
Рівність (9.13) показує, що чим більше відношення
Поиск по сайту: |

 опорі через
опорі через  (рис. 8.4,в).
(рис. 8.4,в).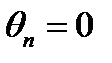 .
.
 ,
,
 ,
,  ,
,  - кути повороту опорних перерізів однопрольотних балок еквівалентної системи на
- кути повороту опорних перерізів однопрольотних балок еквівалентної системи на  опорі від дії одиничних моментів
опорі від дії одиничних моментів  ,
,  ,
,  , а
, а  - від дії зовнішнього навантаження.
- від дії зовнішнього навантаження.
 Рисунок 8.5
Рисунок 8.5

 .
. , тобто взаємний кут повороту опорних перерізів простих балок еквівалентної системи на
, тобто взаємний кут повороту опорних перерізів простих балок еквівалентної системи на  опорі від дії зовнішніх навантажень, зобразимо як суму кутів
опорі від дії зовнішніх навантажень, зобразимо як суму кутів  і
і  зліва і справа від
зліва і справа від  опори (рис. 8.6)
опори (рис. 8.6) .
.
 .
.
 ,
,
 і
і  - моменти інерції відносно осі згину поперечних перерізів n і n+1 прольотів.
- моменти інерції відносно осі згину поперечних перерізів n і n+1 прольотів. Рисунок 8.6
Рисунок 8.6
 і
і  можна знаходити у будь-який спосіб. Дуже зручно користатися відомими узагальненими формулами для типових навантажень, що подані в довідковій літературі.
можна знаходити у будь-який спосіб. Дуже зручно користатися відомими узагальненими формулами для типових навантажень, що подані в довідковій літературі. ,
,
 і
і  - площі епюр згинних моментів, що виникають від заданого зовнішнього навантаження в простих балках з прольотами
- площі епюр згинних моментів, що виникають від заданого зовнішнього навантаження в простих балках з прольотами  і
і  (рис. 8.4);
(рис. 8.4);  і
і  - відстані від центрів ваги вказаних епюр до
- відстані від центрів ваги вказаних епюр до  та
та  опор.
опор. ,
,  ,
,  кожен прольот розглядають як просту балку на двох опорах, що навантажена зовнішнім навантаженням і знайденими опорними моментами
кожен прольот розглядають як просту балку на двох опорах, що навантажена зовнішнім навантаженням і знайденими опорними моментами Рисунок 9.1
Рисунок 9.1
 ,
,  ,
, 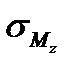 , що діють по одній прямій (лінійний напружений стан) і можуть бути враховані шляхом алгебраїчного сумування
, що діють по одній прямій (лінійний напружений стан) і можуть бути враховані шляхом алгебраїчного сумування .
.
 ,
,  і
і  , що діють в одній площині та спрямовані під кутом одне до одного і можуть бути враховані шляхом геометричного сумування
, що діють в одній площині та спрямовані під кутом одне до одного і можуть бути враховані шляхом геометричного сумування .
.
 Рисунок 9.2
Рисунок 9.2
 на складові по головним осям інерції поперечного перерізу балки
на складові по головним осям інерції поперечного перерізу балки ;
;  .
.
 Рисунок 9.3
Рисунок 9.3
 від сил
від сил 
 а)
а)
 б)
б)
 .
.
 , так щоб вона проходила через центр ваги перерізу і два квадранта, в яких моменти
, так щоб вона проходила через центр ваги перерізу і два квадранта, в яких моменти  .
.
 підставляють зі знаком плюс, якщо в точках першої чверті їм відповідають розтягуючі нормальні напруження, і зі знаком мінус, якщо – стискаючі. Координати точки
підставляють зі знаком плюс, якщо в точках першої чверті їм відповідають розтягуючі нормальні напруження, і зі знаком мінус, якщо – стискаючі. Координати точки  і
і  ,
,
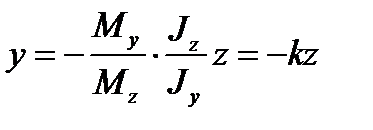 .
.
 .
.
 так, щоб вона проходила через центр ваги перерізу і два квадранта, в яких моменти
так, щоб вона проходила через центр ваги перерізу і два квадранта, в яких моменти 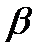 не дорівнює куту
не дорівнює куту  , тобто нейтральна вісь не перпендикулярна площині дії згинного моменту. Вона може бути перпендикулярною до цієї площини лише у випадку
, тобто нейтральна вісь не перпендикулярна площині дії згинного моменту. Вона може бути перпендикулярною до цієї площини лише у випадку  (круг, кільце, квадрат), тому для балок із такими поперечними перерізами поняття косого згину нівелюється.
(круг, кільце, квадрат), тому для балок із такими поперечними перерізами поняття косого згину нівелюється.
 , або
, або  ,
,
 - відстань від довільної точки перерізу до нейтральної осі. Аналіз рівняння (9.6) показує, що найбільші напруження виникають в точках поперечного перерізу, що найбільш віддалені від нейтральної осі (рис. 9.4,б).
- відстань від довільної точки перерізу до нейтральної осі. Аналіз рівняння (9.6) показує, що найбільші напруження виникають в точках поперечного перерізу, що найбільш віддалені від нейтральної осі (рис. 9.4,б). ,
,
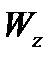 ,
,  - моменти опору перерізу відносно осей
- моменти опору перерізу відносно осей  ,
,
 - величина, якою попередньо задаються.
- величина, якою попередньо задаються. Рисунок 9.5
Рисунок 9.5
 (9.9)
(9.9) , достатньо записати одну з умов (9.9), що відповідає більшому за абсолютною величиною напруженню.
, достатньо записати одну з умов (9.9), що відповідає більшому за абсолютною величиною напруженню. ;
;
 ;
;
 .
.
 Рисунок 9.6
Рисунок 9.6
 .
.
 , тим більша різниця між кутами
, тим більша різниця між кутами  і
і  . Тому, для вузьких і високих перерізів, в яких відношення головних моментів інерції досить велике, вже незначне відхилення площини дії зовнішніх сил від площини найбільшої жорсткості викликає значне відхилення площини згину балки, що слід враховувати при проектуванні.
. Тому, для вузьких і високих перерізів, в яких відношення головних моментів інерції досить велике, вже незначне відхилення площини дії зовнішніх сил від площини найбільшої жорсткості викликає значне відхилення площини згину балки, що слід враховувати при проектуванні.