 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Стійка і нестійка пружна рівновага стиснутого стержня
Під дією стискаючого навантаження, що поступово зростає, стержень проходить три форми рівноваги: стійку, байдужу та нестійку. Очевидна певна аналогія між стійкістю пружної системи і стійкістю положення абсолютно твердого тіла. У стані стійкої рівноваги перебуває важка кулька на дні сферичного заглиблення (рис. 10.1,а). При відхиленні кульки від початкового положення вона після певної кількості коливань повернеться у вихідний стан. Стиснутий стержень перебуває в стані стійкої рівноваги, якщо стискаюча сила Кулька на горизонтальній плоскій поверхні (рис.10.1,б) перебуває в стані байдужої рівноваги, оскільки будь-яке її положення буде однаково стійким. Форма рівноваги стиснутого стержня є байдужою, коли стискаюча сила досягає критичного значення. При цьому стержень може зберегти
Кулька на опуклій поверхні (рис. 10.1,в) перебуває в стані нестійкої рівноваги. У разі виведення кульки з цього положення у вихідний стан вона не повернеться. Стиснутий стержень перебуває в стані нестійкої рівноваги, якщо стискаюча сила перевищує критичне значення. При цьому прямолінійна форма рівноваги стає нестійкою. Втрата стійкості – це відхилення осі стержня від прямолінійної форми рівноваги, спричинене дією стискаючої сили. Стискаюче навантаження, перевищення якого призводить до втрати стійкості вихідної форми стержня, називається критичним. Зазначимо, що втрата стійкості може відбутися навіть тоді, коли напруження під дією критичної сили не досягнуть границі пропорційності. Тому стиснуті стержні обов’язково слід перевіряти не тільки на міцність, а й на стійкість. Для безпечної роботи стиснутих стержнів необхідно, щоб стискаюче навантаження було меншим за критичну силу:
де Величину коефіцієнта запасу стійкості приймають трохи більшою, ніж величину коефіцієнта запасу міцності, оскільки беруть до уваги додаткові несприятливі обставини: початкове викривлення стержня, ексцентриситет прикладання навантаження та ін. Для сталевих стержнів Щоб запобігти втраті стійкості конструкції, необхідно забезпечити виконання умови стійкості (10.1), а для цього потрібно вміти визначити критичне навантаження.
Задача Ейлера
 . Припускається, що напруження під дією критичної сили не перевищують границі пропорційності. У цьому разі стан рівноваги стержня буде байдужим, тобто викривлена форма стержня також буде зрівноваженою. Розглянемо стан стержня із зігнутою віссю, але вважатимемо відхилення від прямої форми неістотним. Тоді диференціальне рівняння осі стержня має вигляд . Припускається, що напруження під дією критичної сили не перевищують границі пропорційності. У цьому разі стан рівноваги стержня буде байдужим, тобто викривлена форма стержня також буде зрівноваженою. Розглянемо стан стержня із зігнутою віссю, але вважатимемо відхилення від прямої форми неістотним. Тоді диференціальне рівняння осі стержня має вигляд
де Рівняння (10.2) запишемо в такому вигляді:
Введемо позначення
Загальний інтеграл цього рівняння є гармонічною функцією
де Шарнірне закріплення кінців стержня виключає відхилення в крайніх його точках, тобто виконуються такі граничні умови: якщо
Стала інтегрування
звідки
де З урахуванням раніше введеного позначення
У розрахунках на стійкість практичне значення має найменша критична сила, що відповідає рівності
Рівняння (10.8) називається формулою Ейлера. Зігнута вісь стержня в стані байдужої рівноваги буде синусоїдою, рівняння якої
де На довжині стержня між кінцевими шарнірами вміщується півхвиля синусоїди, оскільки відхилень не буде при Якщо
вміщує більше ніж одну півхвилю синусоїди відповідно до числа Отже, якщо стискаюча сила Якщо Слід звернути увагу на те, що критична сила не залежить від характеристик міцності матеріалу стержня.
10.3 Вплив умов закріплення стержня на значення критичної сили
де
Величину Коефіцієнти 1) характеру в’язей, що накладені на торцеві і проміжні перерізи стержня; 2) виду навантаження стержня зовнішніми силами (зосереджені чи розподілені) та місця їх прикладання; 3) характеру зміни перерізу стержня по його довжині. Розглянемо вплив першого фактору, тобто вплив умов закріплення стержня. Формулу (10.10) можна отримати, якщо розглянути рівняння поздовжнього згину четвертого порядку
Загальний інтеграл цього рівняння має вигляд
Сталі
Використовуючи ці умови, одержимо систему однорідних рівнянь
Система (10.15) матиме ненульове рішення, якщо її визначник дорівнює нулю:
Розкривши цей визначник, отримаємо трансцендентне рівняння для визначення
Найменший корінь цього рівняння визначає першу критичну силу
Таким чином
 застосоване жорстке затиснення кінців стержня, тоді як у площині більшої жорсткості застосоване жорстке затиснення кінців стержня, тоді як у площині більшої жорсткості  - шарнірне. - шарнірне.
У таких випадках критичною силою для стержня буде менша з двох визначених окремо для кожної з головних площин:
де
10.4 Критичні напруження. Межі застосування формули Ейлера
У стиснутому стержні критичні напруження виникають під дією критичної сили:
Урахувавши, що відношення
Введемо безрозмірну величину
Бачимо, що гнучкість стержня є його узагальненою геометричною характеристикою. Чим вона вища, тим гірше стержень опирається поздовжньому згину. Тепер критичне напруження визначатиметься за формулою
Залежність між критичним напруженням та гнучкістю можна подати у вигляді гіперболічної кривої – гіперболи Ейлера (рис. 10.6). Оскільки формула Ейлера виведена в припущенні, що критичні напруження не перевищують границі пропорційності, існують певні межі її застосування, які визначаються нерівностю
де З нерівності (10.19) визначимо умову, яку повинна задовільняти гнучкість стержня, щоб формула Ейлера була застосовною:
Знак рівності в цій умові відповідає граничній гнучкості
тобто для сталі Ст3 формула Ейлера застосована при
де За формулою Ясинського обчислюють критичні напруження для стержнів середньої гнучкості, що широко використовуються в багатьох сталевих та залізобетонних конструкціях. Для сталевих (Ст3) стержнів середня гнучкість становить Прямо пропорційній залежності між критичним напруженням та гнучкістю для стержнів середньої гнучкості на графіку (див. рис. 10.6) відповідає похила пряма ділянка – так звана пряма Ясинського, що продовжує гіперболу Ейлера. Стержні малої гнучкості
10.5 Практичні розрахунки стиснутих стержнів на стійкість
У розрахунках на стійкість критичне напруження є руйнівним, як границя текучості або границя міцності в розрахунках на міцність. Тому введено поняття допустимого напруження на стійкість
де Умова стійкості вимагає, щоб напруження, яке виникає при стисканні, не перевищувало допустимого напруження на стійкість:
Проте обчислення допустимого напруження на стійкість ускладнюється внаслідок того, що критичне напруження залежить не лише від властивостей матеріалу, а й від гнучкості стержня. Знайдемо залежність між допустимим напруженням на стійкість та допустимим напруженням на міцність при стиску:
де Шукана залежність
де Коефіцієнт Отже, з урахуванням залежності (10.23) умова стійкості набирає вигляду
За допомогою умови стійкості (10.24) розв’язують задачі трьох типів. 1. Перевірка стійкості полягає у перевірці виконання умови стійкості (10.24) в такій послідовності: - визначають мінімальний момент інерції поперечного перерізу стержня та мінімальний радіус інерції (при однаковому закріпленні в головних площинах):
- обчислюють гнучкість стержня за формулою (10.17); - за таблицями вибирають коефіцієнт зменшення основного допустимого напруження - добуті вихідні дані підставляють в умову стійкості (10.24) для перевірки її виконання. 2. Визначення допустимого навантаження з умови стійкості:
виконується аналогічно, за винятком останньої дії, замість чого обчислюють допустиме навантаження з нерівності (10.25). 3. Добір поперечного перерізу стержня, або проектувальний розрахунок, здійснюється на підставі обчислення площі перерізу з умови стійкості:
Ця задача не має єдиного розв’язку, оскільки до нерівності (10.26) входять дві невідомі величини: площа перерізу - беруть довільне значення коефіцієнта
- відповідно до обчисленої площі визначають розміри перерізу або вибирають номер профілю із сортаменту; - визначають радіус інерції та гнучкість стержня, за якою з таблиць знаходять j1*; - порівнюють коефіцієнти j1 та j1* і, якщо розбіжність невелика, перевіряють умову стійкості (10.24); у разі істотної розбіжності значень j1 та j1* виконують друге наближення, для якого оптимальним значенням коефіцієнта зниження основного допустимого напруження j2 буде середньоарифметичне
Після цього повторюють всі зазначені дії. Щоб отримати задовільний розв’язок, здебільшого треба виконати кілька наближень.
11 РОЗРАХУНКИ НА МІЦНІСТЬ ПРИ НАПРУЖЕННЯХ, ЩО ЗМІНЮЮТЬСЯ Поняття про втому
Якщо на елемент конструкції діє навантаження, яке з часом багаторазово змінюється за модулем та напрямом, то характер опору матеріалу істотно відрізняється від опору дії статичного навантаження. Побутовим прикладом такого навантажування може бути багаторазове згинання відрізка дроту при намаганні його зламати. Очевидно, що волокна дроту поперемінно опиняються то в розтягнутій, то в стиснутій зонах (рис. 11.1).
Явище зниження міцності чи руйнування матеріалу під тривалою дією напружень, що циклічно змінюються в часі називають втомою. Здатність матеріалів і конструкцій опиратися дії повторних (циклічних) навантажень називають витривалістю. Втома є наслідком виникнення зсувів та зародження мікротріщин в несприятливо орієнтованих структурних складових матеріалу (зернах кристалів у металах, волокнах і матриці композитів, молекулярних ланцюгах полімерів і т.д.). Збільшуючись, мікротріщини зливаються в одну магістральну тріщину (макротріщину). Коли розміри магістральної тріщини досягають так званих критичних розмірів, вона починає спонтанно зростати, що призводить до руйнування деталі чи зразка. Розрізняють два види втоми: - багатоциклова, що характеризується пошкодженням і руйнуванням матеріалу внаслідок великого числа циклів навантаження (більше 105) при напруженнях, що менші границі текучості; - малоциклова, що спостерігається при відносно малому числі циклів (103 – 105), коли діючі навантаження викликають пластичні деформації. Ми розглянемо лише багатоциклову втому. Розвиток теорії витривалості проходить переважно шляхом накопичення і систематизації експериментальних даних. На сьогодні ми можемо розраховувати на витривалість порівняно вузьке коло деталей, щоправда таких, які часто зустрічаються (вали, зубчаті колеса, різьові з’єднання і ін.). Для розрахунку нових вузлів і систем доводиться виконувати натурні втомні випробування.
Поиск по сайту: |
 не перевищує критичного значення
не перевищує критичного значення  Рисунок 10.1
Рисунок 10.1
 ,
,
 - коефіцієнт запасу стійкості.
- коефіцієнт запасу стійкості. ; для дерев’яних стержнів
; для дерев’яних стержнів  .
. Рисунок 10.3
Рисунок 10.3
 Рисунок 10.2
Рисунок 10.2
 ,
,
 - мінімальний момент інерції поперечного перерізу стержня;
- мінімальний момент інерції поперечного перерізу стержня;  - відхилення центра ваги довільного перерізу від початкового положення на прямій осі;
- відхилення центра ваги довільного перерізу від початкового положення на прямій осі;  - згинний момент у довільному перерізі зігнутого стержня.
- згинний момент у довільному перерізі зігнутого стержня. .
.
 і дістанемо лінійне однорідне диференціальне рівняння
і дістанемо лінійне однорідне диференціальне рівняння .
.
 ,
,
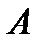 та
та  - сталі інтегрування, які визначаються з умов закріплення кінців стержня, тобто з граничних умов.
- сталі інтегрування, які визначаються з умов закріплення кінців стержня, тобто з граничних умов. , то
, то  , якщо
, якщо  , то
, то  . Підставивши граничні умови в розв’язок (10.4), дістанемо систему двох рівнянь
. Підставивши граничні умови в розв’язок (10.4), дістанемо систему двох рівнянь ;
;  .
.
 ,
,
 ,
,
 - довільне ціле число.
- довільне ціле число. із співвідношення (10.6) визначимо множину критичних сил:
із співвідношення (10.6) визначимо множину критичних сил: .
.
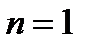 :
: .
.
 ,
,
 та
та  .
. більше за одиницю, то зігнута вісь стержня, що описується рівнянням
більше за одиницю, то зігнута вісь стержня, що описується рівнянням ,
,
 (рис. 10.3). В таких умовах потрібна більша критична сила, щоб утримати стержень у зігнутому стані з
(рис. 10.3). В таких умовах потрібна більша критична сила, щоб утримати стержень у зігнутому стані з  , то стержень має лише одну – прямолінійну форму рівноваги, що є стійкою.
, то стержень має лише одну – прямолінійну форму рівноваги, що є стійкою. , то поряд із прямолінійною існує інша – криволінійна форма рівноваги, причому прямолінійна форма рівноваги нестійка, а стійкою є викривлена форма рівноваги. В таких випадках кажуть, що відбувається біфуркація рівноважних станів стержня.
, то поряд із прямолінійною існує інша – криволінійна форма рівноваги, причому прямолінійна форма рівноваги нестійка, а стійкою є викривлена форма рівноваги. В таких випадках кажуть, що відбувається біфуркація рівноважних станів стержня. Рис.10.4
Рис.10.4
 ,
або
,
або
 ,
,
 - коефіцієнт зведення довжини стержня (коефіцієнт Ясинського), що чисельно рівний величині, оберненій числу півхвиль синусоїди, по якій згинається стержень;
- коефіцієнт зведення довжини стержня (коефіцієнт Ясинського), що чисельно рівний величині, оберненій числу півхвиль синусоїди, по якій згинається стержень;  - коефіцієнт стійкості, що визначають за формулою
- коефіцієнт стійкості, що визначають за формулою .
.
 називають зведеною довжиною. Це умовна довжина шарнірно обіпертого стержня, для якого критична сила дорівнює критичній силі для заданого стержня довжиною
називають зведеною довжиною. Це умовна довжина шарнірно обіпертого стержня, для якого критична сила дорівнює критичній силі для заданого стержня довжиною 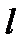 .
. і
і  залежать від трьох факторів:
залежать від трьох факторів: .
.
 .
.
 визначають з граничних умов. Наприклад, для другого випадку закріплення (рис. 10.4,б):
визначають з граничних умов. Наприклад, для другого випадку закріплення (рис. 10.4,б): ;
;  ;
;  ;
;  .
.
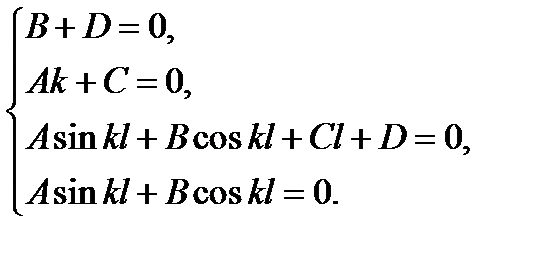
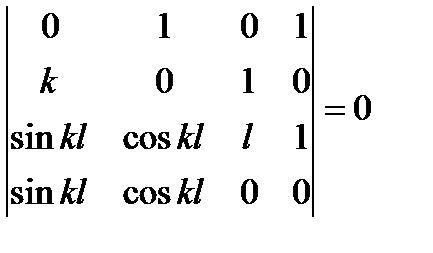 .
.
 :
: .
.
 , тоді
, тоді .
.
 ;
;  . Аналогічно отримують значення коефіцієнтів, що вказані на рис. 10.4, при інших способах закріплення стержня.
. Аналогічно отримують значення коефіцієнтів, що вказані на рис. 10.4, при інших способах закріплення стержня. Рисунок 10.5
Рисунок 10.5
 ;
;  ,
,
 та
та 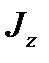 - головні моменти інерції перерізу стержня.
- головні моменти інерції перерізу стержня. .
.
 є квадратом мінімального радіуса інерції
є квадратом мінімального радіуса інерції  , одержимо
, одержимо .
.
 , що називається гнучкістю стержня і дорівнює відношенню зведеної довжини до мінімального радіуса інерції поперечного перерізу:
, що називається гнучкістю стержня і дорівнює відношенню зведеної довжини до мінімального радіуса інерції поперечного перерізу: .
.
 .
.
 ,
,
 - границя пропорційності матеріалу стержня.
- границя пропорційності матеріалу стержня. .
.
 , при зменшенні якої формула Ейлера стає непридатною. Бачимо, що гранична гнучкість стержня є його фізико-механічною характеристикою і залежить від модуля пружності і границі пропорційності. Для стержнів, виготовлених з маловуглецевої сталі Ст3, при модулі пружності
, при зменшенні якої формула Ейлера стає непридатною. Бачимо, що гранична гнучкість стержня є його фізико-механічною характеристикою і залежить від модуля пружності і границі пропорційності. Для стержнів, виготовлених з маловуглецевої сталі Ст3, при модулі пружності  і границі пропорційності
і границі пропорційності  гранична гнучкість
гранична гнучкість ,
,
 . Відповідно для матеріалів з іншими механічними характеристиками граничні гнучкості матимуть інші значення.
. Відповідно для матеріалів з іншими механічними характеристиками граничні гнучкості матимуть інші значення. Рисунок 10.6
Рисунок 10.6
 ,
,
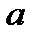 ,
,  та
та  - коефіцієнти, що залежать від матеріалу стержня і визначаються експериментально (для пластичних матеріалів
- коефіцієнти, що залежать від матеріалу стержня і визначаються експериментально (для пластичних матеріалів  ).
). .
. на стійкість не розраховують, оскільки відповідні критичні напруження для них перевищують границю текучості, тобто руйнування таких стержнів відбувається внаслідок втрати міцності (рис.10.6 ділянка паралельна осі абсцис).
на стійкість не розраховують, оскільки відповідні критичні напруження для них перевищують границю текучості, тобто руйнування таких стержнів відбувається внаслідок втрати міцності (рис.10.6 ділянка паралельна осі абсцис). :
: ,
,
 .
.
 ,
,
 - допустиме напруження на міцність при стисканні;
- допустиме напруження на міцність при стисканні;  - коефіцієнт запасу міцності.
- коефіцієнт запасу міцності. ,
,
 - коефіцієнт зменшення основного допустимого напруження на міцність при розрахунку на стійкість.
- коефіцієнт зменшення основного допустимого напруження на міцність при розрахунку на стійкість. для кожного матеріалу можна визначити при будь-якому значенні гнучкості й подати у вигляді таблиці або графіку залежності
для кожного матеріалу можна визначити при будь-якому значенні гнучкості й подати у вигляді таблиці або графіку залежності  від
від 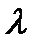 .
. .
.
 ;
;
 ;
;
 .
.
 та коефіцієнт
та коефіцієнт  , який залежить від невизначених ще розмірів перерізу, його форми та довжини стержня. Тому задачу розв’язують методом послідовних наближень з перевіркою проміжних результатів за допомогою умови стійкості в такій послідовності:
, який залежить від невизначених ще розмірів перерізу, його форми та довжини стержня. Тому задачу розв’язують методом послідовних наближень з перевіркою проміжних результатів за допомогою умови стійкості в такій послідовності: та обчислюють площу
та обчислюють площу  перерізу стержня:
перерізу стержня: ;
;
 .
.
 Рисунок 11.1
Рисунок 11.1