 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Внутренняя энергия и теплоемкость электронного газа в металле
Каждый электрон металла движется в поле, создаваемом всеми ядрами и остальными электронами металла. В грубом приближении можно принять, что ядра и остальные электроны образуют в объеме металла некоторое постоянное, не зависящее от координат, поле. Электроны, однако, не могут не иметь кинетической энергии в этом поле даже при абсолютном нуле. Состояние, при котором они все имели бы скорость, равную нулю, противоречило бы принципу Паули. Определим кинетическую энергию электронного газа при абсолютном нуле. При этом электроны заполняют области фазового пространства от импульса, равного нулю, до некоторого наибольшего значения рт Общий объем фазового пространства, занимаемый электронами, должен равняться Nh3/2, так как в каждой ячейке объемом h3 помещаются два электрона с насыщенными спинами, а число электронов равно N. Таким образом, 4πp
V/3 = Nh3/2 и pm = 3√(3h3/8π)n, (XIII.29) где n = N/V(V - объем, в котором находятся электроны). Число электронов, имеющих импульс в интервале между р и p + dp, составит 4πp2Vdp/(h3/2). Таким образом, кинетическая энергия электронного газа при абсолютном нуле будет
Величина Екин, носящая название нулевой энергии электронного газа, растет с плотностью газа. Интересно сравнить среднюю энергию Eкин/N с максимальной энергией. Согласно уравнению (XIII.29):
а согласно уравнению (ХIII.30)
отсюда ε = 3/5εm. (XIII.32) Нулевые энергии электронов в металлах очень велики. Если подставить в уравнение (XIII.31) значение числа электронов в единице объема (n) для серебра, то окажется, что для одного моля электронов Eкин = 288000 Дж/моль: Найдем температуру, при которой, согласно закону распределения по степеням свободы, газ мог бы иметь такую энергию: 288000 = 3RT/2 и T = 23000 К. Несмотря на большую энергию электронного газа, теплоемкость его равна нулю, так как вследствие вырождения эта энергия не зависит от температуры. По мере повышения температуры вырождение будет сниматься и энергия электронного газа начнет медленно увеличиваться с повышением температуры. Расчет показывает, что при низких температурах энергия электронного газа может быть описана следующей формулой:
Для вырожденного электронного газа в металлах теплоёмкость определяется формулой
где m * — эффективная масса электронов, Теплоёмкость стремится к нулю при малых температурах, удовлетворяя теореме Нернста и линейно возрастает с температурой. Поскольку теплоёмкость кристаллической решётки при низких температурах пропорциональная кубу температуры (см. модель Дебая) то существует область низких температур, при которых теплоёмкость электронов больше чем теплоёмкость решётки. Однако при более высоких температурах, чем температура Дебая, вклад электронной подсистемы в общую теплоёмкость твёрдого тела не превышает нескольких процентов. Для этих температур справедливо
где Объясняется такое соотношение тем, что вклад в электронную теплоёмкость вносят лишь те электроны, которые имеют энергию, близкую к энергии Ферми. Электроны с энергиями, намного низшими чем энергия уровня Ферми, не могут получать тепло, поскольку для увеличения энергии им нужно было бы перейти на близкие энергетические уровне внутри зоны, уже занятые другими электронами. Из-за принципа Паули переход в занятое другим электроном состояние невозможен. 4. Электропроводность металлов. Квантовая теория электропроводности металлов - теория электропроводности, основывающаяся на квантовой механике и квантовой статистике Ферми - Дирака, - пересмотрела вопрос об электропроводности металлов, рассмотренный в классической физике. Расчет электропроводности металлов, выполненный на основе этой теории, приводит к выражению для удельной электрической проводимости металла
которое по внешнему виду напоминает классическую формулу (103.2) для g, но имеет совершенно другое физическое содержание. Здесь n- концентрация электронов проводимости в металле, álFñ - средняя длина свободного пробега электрона, имеющего энергию Ферми, áuFñ - средняя скорость теплового движения такого электрона. Выводы, получаемые на основе формулы (238.1), полностью соответствуют опытным данным. Квантовая теория электропроводности металлов, в частности, объясняет зависимость удельной проводимости от температуры: g~ 1/T(классическая теория (см. § 103) дает, что g ~ 1/ÖT, а также аномально большие величины (порядка сотен периодов решетки) средней длины свободного пробега электронов в металле (см. § 103). Квантовая теория рассматривает движение электронов с учетом их взаимодействия с кристаллической решеткой. Согласно корпускулярно-волновому дуализму, движению электрона сопоставляют волновой процесс. Идеальная кристаллическая решетка (в ее узлах находятся неподвижные частицы и в ней отсутствуют нарушения периодичности) ведет себя подобно оптически однородной среде - она «электронные волны» не рассеивает. Это соответствует тому, что металл не оказывает электрическому току - упорядоченному движению электронов - никакого сопротивления. «Электронные волны», распространяясь в идеальной кристаллической решетке, как бы огибают узлы решетки и проходят значительные расстояния. В реальной кристаллической решетке всегда имеются неоднородности, которыми могут быть, например, примеси, вакансии; неоднородности обусловливаются также тепловыми колебаниями. В реальной кристаллической решетке происходит рассеяние «электронных волн» на неоднородностях, что и является причиной электрического сопротивления металлов. Рассеяние «электронных волн» на неоднородностях, связанных с тепловыми колебаниями, можно рассматривать как столкновения электронов с фононами. Согласно классической теории, áuFñ ~ ÖT, поэтому она не смогла объяснить истинную зависимость у от температуры (см. § 103). В квантовой теории средняя скорость áuFñ от температуры практически не зависит, так как доказывается, что с изменением температуры уровень Ферми остается практически неизменным. Однако с повышением температуры рассеяние «электронных волн» на тепловых колебаниях решетки (на фононах) возрастает, что соответствует уменьшению средней длины свободного пробега электронов. В области комнатных температур álFñ ~ Т-1, поэтому, учитывая независимость áuñ от температуры, получим, что сопротивление металлов (R ~ l/g)в соответствии с данными опытов растет пропорционально Т. Таким образом, квантовая теория электропроводности металлов устранила и эту трудность классической теории. 5. Сверхпроводимость.
Рис. 3. Кривая намагничивания сверхпроводников 1-го рода
Рис. 4. Кривая намагничивания сверхпроводников 2-го рода
Рис. 5. Фазовая диаграмма для сверхпроводников
Рис. 6. Скачок теплоёмкости сверхпроводника 1–3 из 6 Сверхпроводимость, свойство многих проводников, состоящее в том, что их электрическое сопротивление скачком падает до нуля при охлаждении ниже определённой критической температуры Тк, характерной для данного материала. С. обнаружена у более чем 25 металлических элементов, у большого числа сплавов и интерметаллических соединений, а также у некоторых полупроводников. Рекордно высоким значением Тк (около 23 К) обладает соединение Nb3Ge. Основные явления. Скачкообразное исчезновение сопротивления при понижении температуры впервые наблюдал X. Камерлинг-Оннес (1911) на ртути (рис. 1). Он пришёл к выводу, что ртуть при Т = 4,15 К переходит в новое состояние, которое вследствие его необычных электрических свойств может быть названо сверхпроводящим. Несколько позднее Камерлинг-Оннес обнаружил, что электрическое сопротивление ртути восстанавливается при включении достаточно сильного магнитного поля (его называют критическим магнитным полем Нк). Измерения показали, что падение сопротивления до нуля происходит на протяжении очень узкого, но конечного интервала температур. Ширина этого интервала для чистых образцов составляет 10-3 — 10-4 К и возрастает при наличии примесей и других дефектов структуры. Отсутствие сопротивления в сверхпроводящем состоянии с наибольшей убедительностью демонстрируется опытами, в которых в сверхпроводящем кольце возбуждается ток, практически не затухающий с течением времени. В одном из вариантов опыта используются два кольца из сверхпроводящего металла. Большее из колец неподвижно закрепляется, а меньшее концентрически подвешивается на упругой нити таким образом, что когда нить не закручена, плоскости колец образуют между собой некоторый угол. Кольца охлаждаются в присутствии магнитного поля ниже температуры Тк, после чего поле выключается. При этом в кольцах возбуждаются токи, взаимодействие между которыми стремится уменьшить первоначальный угол между плоскостями колец. Нить закручивается, а наблюдаемое постоянство угла закручивания показывает, что токи в кольцах являются незатухающими. Опыты такого рода позволили установить, что сопротивление металла в сверхпроводящем состоянии меньше чем 10-20 ом×см (сопротивление чистых образцов меди или серебра составляет около 10-9 ом×см при температуре жидкого гелия). Однако сверхпроводник не является просто идеальным проводником, как это считалось ещё в течение более чем 20 лет после открытия С. Существование значительно более глубокого различия между нормальным и сверхпроводящим состояниями металла стало очевидным, после того как нем. физики В. Мейснер и Р. Оксенфельд (1933) установили, что слабое магнитное поле не проникает в глубь сверхпроводника. Особенно важно, что это имеет место независимо от того, было ли поле включено до или после перехода металла в сверхпроводящее состояние. В отличие от этого, идеальный проводник (т. е. проводник с исчезающе малым сопротивлением) должен захватывать пронизывающий его магнитный поток. Это различие иллюстрирует рис. 2 (а, б, в), на котором схематически изображено распределение поля вблизи односвязного металлического образца на трёх последовательных этапах опыта: а) образец находится в нормальном состоянии, внешнее поле свободно проникает в глубь металла; б) образец охлаждается ниже Тк, магнитное поле выталкивается из сверхпроводника (верхний рисунок), тогда как в случае идеального проводника распределение поля оставалось бы неизменным (нижний рисунок); в) внешнее поле выключается, при этом исчезает и намагниченность сверхпроводника. В случае идеального проводника поток магнитной индукции через образец сохранил бы свою величину, и картина поля была бы такой же, как у постоянного магнита. Выталкивание магнитного поля из сверхпроводящего образца (это явление обычно называют эффектом Мейснера) означает, что в присутствии внешнего магнитного поля такой образец ведёт себя как идеальный диамагнетик той же формы с магнитной восприимчивостью c= —1/4p. В частности, если образец имеет форму длинного сплошного цилиндра, а внешнее поле Н однородно и параллельно оси цилиндра, то магнитный момент, отнесённый к единице объёма, будет равен М = —Н/4p. Это примерно в 105 раз больше по абсолютной величине, чем удельная намагниченность диамагнитного металла в нормальном состоянии. Эффект Мейснера связан с тем, что при Н < Нк в поверхностном слое сверхпроводящего цилиндра появляется круговой незатухающий ток, сила которого как раз такова, что магнитное поле этого тока компенсирует внешнее поле в толще сверхпроводника. Опыт показывает, что в случае больших образцов слабое магнитное поле в условиях эффекта Мейснера проникает в металл на глубину d ~ 10-5—10-6 см, именно в этом слое течёт поверхностный токоло По своему поведению в достаточно сильных полях сверхпроводники подразделяются на две большие группы, т. н. сверхпроводники 1-го и 2-го рода. На рис. 3 и 4 в несколько идеализированной форме изображены кривые намагничивания М (Н), типичные для каждой из этих групп. Кривые относятся к случаю длинных цилиндрических образцов, помещенных в поле, параллельное оси цилиндра. При такой геометрии опыта отсутствуют эффекты размагничивания, и картина поэтому является наиболее простой. Начальный прямолинейный участок на этих кривых, где М =—Н/4p, соответствует интервалу значений Н, на котором имеет место эффект Мейснера. Как видно из рисунка, дальнейший ход кривых М (Н) для сверхпроводников 1-го и 2-го рода существенно различается. Сверхпроводники 1-го рода, которыми являются все достаточно чистые сверх-проводящие металлические элементы (за исключением V и Nb), теряют С. при поле Н = Нк, когда поле скачком проникает в металл и он во всём объёме переходит в нормальное состояние. При этом удельный магнитный момент также скачком уменьшается примерно в 105 раз. Критическому полю Нк можно дать простое термодинамическое истолкование. При температуре Т < Тк и в отсутствии магнитного поля свободная энергия в сверхпроводящем состоянии Fc ниже, чем в нормальном Fн. При включении поля свободная энергия сверхпроводника возрастает на величину H 2/8p, равную работе намагничивания, и при Н = Нк сравнивается с Fн (в силу малости магнитного момента в нормальном состоянии Fн практически не изменяется при включении поля). Т. о., поле Нк определяется из условия равновесия в точке перехода: Fc + Н 2к/8p = Fн. (1) Критическое поле Нк зависит от температуры: оно максимально при Т = 0 и монотонно убывает до нуля по мере приближения к Тк. (Значения Нк для некоторых сверхпроводников приведены в ст. Сверхпроводники.) На рис. 5 изображена фазовая диаграмма на плоскости (Н, Т). Заштрихованная область, ограниченная кривой Нк (Т), соответствует сверхпроводящему состоянию. По измеренной зависимости Нк (Т) могут быть рассчитаны все термодинамические характеристики сверхпроводника 1-го рода. В частности, из формулы (1) непосредственно получается (при дифференцировании по температуре) выражение для теплоты фазового перехода в сверхпроводящее состояние: где S — энтропия единицы объёма. Знак Q таков, что теплота поглощается сверхпроводником при переходе в нормальное состояние. Поэтому если разрушение С. магнитным полем производится при адиабатической изоляции образца, то последний будет охлаждаться. Скачкообразный характер фазового перехода в магнитном поле (рис. 3) наблюдается только в случае весьма специальной геометрии опыта: длинный цилиндр в продольном поле. При произвольной форме образца и др. ориентациях поля переход оказывается растянутым по более или менее широкому интервалу значений Н: он начинается при Н < Нк и заканчивается, когда поле во всех точках образца превысит Нк. В этом интервале значений Н сверхпроводник 1-го рода находится в т. н. промежуточном состоянии. Он расслаивается на чередующиеся области нормальной и сверхпроводящей фаз, причём так, что поле в нормальной фазе вблизи границы раздела параллельно этой границе и равно Нк. По мере увеличения поля возрастает доля нормальной фазы и происходит уменьшение магнитного момента образца. Структура расслоения и характер кривой намагничивания существенно зависят от геометрических факторов. В частности, для пластинки, ориентированной перпендикулярно магнитному полю, расслоение начинается уже в слабом поле, гораздо меньшем, чем Нк. С магнитными свойствами сверхпроводников тесно связаны и особенности протекания в них тока. В силу эффекта Мейснера ток является поверхностным, он сосредоточен в тонком слое, определяемом глубиной проникновения магнитного поля. Когда ток достигает некоторой критической величины, достаточной для создания критического магнитного поля, сверхпроводник 1-го рода переходит в промежуточное состояние и приобретает электрическое сопротивление. К сверхпроводникам 2-го рода относится большинство сверхпроводящих сплавов. Кроме того, сверхпроводниками 2-го рода становятся и сверхпроводящие металлические элементы (сверхпроводники 1-го рода) при введении в них достаточно большого количества примесей. Картина разрушения сверхпроводимости магнитным полем является у этих сверхпроводников более сложной. Как видно из рис. 4, даже в случае цилиндрического образца в продольном поле происходит постепенное уменьшение магнитного момента на протяжении значительного интервала полей от Нк, когда поле начинает проникать в толщу образца, и до поля Нк, при котором происходит полное разрушение сверхпроводящего состояния. В большинстве случаев кривая намагничивания такого типа является необратимой (наблюдается магнитный гистерезис). Величина гистерезиса очень чувствительна к технологии приготовления образцов, и в некоторых случаях путём специальной обработки удаётся получить образцы с почти обратимой кривой намагничивания. Поле Нк часто оказывается весьма большим, достигая сотен тысяч эрстед (см. статьи Магниты сверхпроводящие и Сверхпроводники). Что же касается термодинамического критического поля Нк, определяемого соотношением (1), то оно для сверхпроводников 2-го рода не является непосредственно наблюдаемой характеристикой. Однако его можно рассчитать, исходя из найденных опытным путём значений свободной энергии в нормальном и сверхпроводящем состояниях в отсутствии магнитного поля. Оказывается, что вычисленное таким способом значение Нк попадает в интервал между Фазовый переход в сверхпроводящее состояние в отсутствии магнитного поля.Прямые измерения теплоёмкости сверхпроводников при Н = 0 показывают, что при понижении температуры теплоёмкость в точке перехода Тк испытывает скачок до величины, которая примерно в 2,5 раза превышает её значение в нормальном состоянии в окрестности Тк (рис. 6). При этом теплота перехода Q = 0, что следует, в частности, из формулы (2) (Нк = 0 при Т = Тк). Т. о., переход из нормального в сверхпроводящее состояние в отсутствии магнитного поля является фазовым переходом 2-го рода. Из формулы (2) можно получить важное соотношение между скачком теплоёмкости и углом наклона кривой Нк (Т)(рис. 5) в точке Т = Тк: где Сс и Сн— значения теплоёмкости в сверхпроводящем и нормальном состояниях. Это соотношение с хорошей точностью подтверждается экспериментом. Природа сверхпроводимости. Совокупность экспериментальных фактов о С. убедительно показывает, что при охлаждении ниже Тк проводник переходит в новое состояние, качественно отличающееся от нормального. Исследуя различные возможности объяснения свойств сверхпроводника, особенно эффекта Мейснера, немецкие учёные, работавшие в Англии, Г. и Ф. Лондоны (1934) пришли к заключению, что сверхпроводящее состояние является макроскопическим квантовым состоянием металла. На основе этого представления они создали феноменологическую теорию, объясняющую поведение сверхпроводников в слабом магнитном поле — эффект Мейснера и отсутствие сопротивления. Обобщение теории Лондонов, сделанное Гинзбургом и Ландау (1950), позволило рассмотреть вопросы, относящиеся к поведению сверхпроводников в сильных магнитных полях. При этом было объяснено огромное количество экспериментальных данных и предсказаны новые важные явления. Убедительным подтверждением правильности исходных предпосылок упомянутых теорий явилось открытие эффекта квантования магнитного потока, заключённого внутри сверхпроводящего кольца. Из уравнений Лондонов следует, что магнитный поток в этом случае может принимать лишь значения, кратные кванту потока Фо = hc/e*, где е* — заряд носителей сверхпроводящего тока, h — Планка постоянная, с — скорость света. В 1961 Р. Долл и М. Небауэр и, независимо, Б. Дивер и У. Фейроенк (США) обнаружили этот эффект. Оказалось, что е* = 2e, где е — заряд электрона. Явление квантования магнитного потока имеет место и в случае упомянутого выше состояния сверхпроводника 2-го рода в магнитном поле, большем, чем Нк1. Образующиеся здесь нити нормальной фазы несут квант потока Фо. Найденная в опытах величина заряда частиц, создающих своим движением сверхпроводящий ток (е* = 2e), подтверждает Купера эффект, на основе которого в 1957 Дж. Бардин, Л. Купер и Дж. Шриффер (США) и Н. Н. Боголюбов (СССР) построили последовательную микроскопическую теорию С. Согласно Куперу, два электрона с противоположными спинами при определённых условиях могут образовывать связанное состояние (куперовскую пару). Заряд такой пары равен 2e. Пары обладают нулевым значением спина и подчиняются Бозе — Эйнштейна статистике. Образуясь при переходе металла в сверхпроводящее состояние, пары испытывают т. н. бозе-конденсацию (см. Квантовая жидкость), и поэтому система куперовских пар обладает свойством сверхтекучести. Т. о., С. представляет собой сверхтекучесть электронной жидкости. При Т = 0 связаны в пары все электроны проводимости. Энергия связи электронов в паре весьма мала: она равна примерно 3,5 kTk, где k — Больцмана постоянная. При разрыве пары, происходящем, например, при поглощении кванта электромагнитного поля или кванта звука (фонона), в системе возникают возбуждения. При отличной от нуля температуре имеется определённая равновесная концентрация возбуждений, она возрастает с температурой, а концентрация пар соответственно уменьшается. Энергия связи пары определяет т. н. щель в энергетическом спектре возбуждений, т. е. минимальную энергию, необходимую для создания отдельного возбуждения. Природа сил притяжения между электронами, приводящих к образованию пар, вообще говоря, может быть различной, хотя у всех известных сверхпроводников эти силы определяются взаимодействием электронов с фононами. Тем не менее развитие теории С. стимулировало интенсивные теоретические поиски других механизмов С. В этом плане особое внимание уделяется т. н. нитевидным (одномерным) и слоистым (двумерным) структурам, обладающим достаточно большой проводимостью, в которых имеются основания ожидать более интенсивного притяжения между электронами, чем в обычных сверхпроводниках, а следовательно, — и более высокой температуры перехода в сверхпроводящее состояние. Явления, родственные С., по-видимому, могут иметь место и в некоторых космических объектах, например в нейтронных звёздах. Практическое применение сверхпроводимости интенсивно расширяется. Наряду с магнитами сверхпроводящими, сверхпроводящими магнитометрами существует ряд других технических устройств и измерительных приборов, основанных на использовании различных свойств сверхпроводников (см. Криоэлектроника). Построены сверхпроводящие резонаторы, обладающие рекордно высокой (до 1010) добротностью, сверхпроводящие элементы для ЭВМ, перспективно применение сверхпроводников в крупных электрических машинах и т. д. Эффект Джозсфсона. ДЖОЗЕФСОНА ЭФФЕКТ - протекание сверхпроводящего тока через тонкую изолирующую или несверхпроводящую прослойку между двумя сверхпроводниками (т. н. джозефсоновский контакт). Эффект был теоретически предсказан Б. Джозефсоном (В. Josephson, 1962) [1]. Д. э. обнаруживается при изучении вольт-амперной характеристики (BAX) джозефсоновских контактов (ДК). При пропускании через ДК достаточно слабого тока напряжение на контакте отсутствует, т. е. ток является чисто сверхпроводящим (джозефсоновский ток). Его существование связано с неполным разрушением куперовских пар электронов (см. Купера эффект) при их прохождении через очень тонкую несверхпроводящую прослойку. Такой режим называется стационарным Д. э. (экспериментально обнаружен в 1963 [2]). При увеличении тока через контакт и достижении им нек-рой величины IC на контакте возникает напряжение. Значение критич. джозеф-соновского тока IС зависит от свойств контакта, темп-ры и магн. поля. Ток IС складывается из тока сверхпроводящих (спаренных) электронов, к-рый теперь становится переменным (его частота зависит от напряжения на контакте), и тока, обусловленного прохождением через прослойку нормальных (несверхпроводящих) электронов. Режим при токе IС наз. нестационарным Д. э. Согласно теории сверхпроводимости, сверхпроводящие (спаренные) электроны характеризуются единой волновой функцией, фаза к-рой плавно меняется вдоль сверхпроводника при протекании по нему тока (фазовая когерентность сверхпроводящих электронов). При прохождении сверхпроводящих электронов через несверхпроводящую прослойку фазовая когерентность частично (в меру отношения толщины прослойки к т. н. длине когерентности) разрушается и протекание джозефсоновского тока через прослойку сопровождается скачком фазы волновой ф-ции сверхпроводящих электронов на этой прослойке
Из ф-лы (1) видно,что джозефсоновский ток не может превышать IС. Величина IС и механизм прохождения электронов через прослойку зависят от типа прослойки. Одним из типичных примеров ДК является туннельный контакт, состоящий из двух одинаковых или разл. сверхпроводников (обычно в виде тонких плёнок), разделённых очень тонким слоем диэлектрика, напр. слоем окисла материала одного из сверхпроводящих электродов. Протекание тока через прослойку в этом случае обусловлено квантовым туннелированием электронов (см. Туннельный эффект) через непроводящий барьер. Для получения измеримого джозефсоновского тока толщина изолирующей прослойки должна быть ок. 10-20 А. На рис. для примера изображена типичная BAX для туннельного контакта из одинаковых сверхпроводников. Стрелками показано направление изменения тока. Если увеличивать ток, то происходит описанный выше переход из стационарного в нестационарный режим Д. э. При уменьшении тока нестационарный Д. э. может сохраниться до значений тока, меньших критического (т. е. туннельный контакт проявляет гистерезис).
Вольт-амперная характеристика (BAX) туннельного контакта Sn- Sn при температуре 1,4 К (прослойка - плёнка оксида олова). При нестационарном Д. э. разность фаз на контакте зависит от времени:
где V - напряжение на контакте, е - заряд электрона. Ур-ние (2) является следствием Шрёдингера уравнения для волновой ф-ции пары сверхпроводящих электронов при наличии постоянной потенц. энергии 2eV и не связано с наличием прослойки, а имеет общий характер. Частота w сверхпроводящего тока через контакт определяется соотношением:
Соотношения (2) и (3) называются соотношениями Джозефсона. Нестационарный Д. э можно рассматривать также как прохождение сверхпроводящих электронов через прослойку, сопровождающееся изменением их энергии на величину 2eV в расчёте на каждую куперовскую пару. При этом процессе испускаются кванты эл.- магн. излучения с частотой
(п - целое число), прохождение сверхпроводящих электронов через контакт происходит с поглощением п фотонов внеш. поля, что приводит к появлению дополнит. тока через контакт, т. е. к возникновению на BAX участков с нулевым дифференциальным сопротивлением. Наблюдение таких участков и явилось первым косвенным обнаружением нестационарного Д. э. в 1963 [3]. Прямое наблюдение генерации СВЧ-излучения джозефсоновским контактом, находящимся под пост. напряжением, было осуществлено в 1965 [4]. Кроме туннельных структур джозефсоновские контакты могут представлять собой т. н. слабосвязанные сверхпроводники, т. е. два сверхпроводника, соединённых узким и коротким сверхпроводящим или нормальным "мостиком", тонкой прослойкой нормального металла либо с помощью точечного контакта. Аналог нестационарного Д. э. наблюдается также в очень узких однородных сверхпроводящих проволочках, где джозефсоновская генерация возникает при пропускании достаточно большого тока. Совокупность явлений, связанных с Д. э. в разл. системах, носит назв. слабой сверхпроводимости [5,6,7]. Д. э. подтверждает осн. концепцию совр. теории сверхпроводимости - наличие единой волновой ф-ции и фазовой когерентности спаренных электронов в сверхпроводящем состоянии. По своей доступности эксперим. исследованию Д. э. представляет собой одну из уникальных возможностей изучать проявления квантовых свойств микромира в макроскопич. масштабе. Д. э. используют в целом ряде криогенных приборов. Соотношение (1) является основой практич. использования стационарного Д. э. в т. н. сверхпроводящих квантовых интерферометрах (сквидах). ДК могут применяться в качестве генераторов и -детекторов СВЧ-диапазона. Свойство ДК переключаться с нулевого на конечное напряжение при превышении током критич. значения в совокупности с малой ёмкостью позволяет использовать их в качестве быстродействующих логич. элементов ЭВМ [7, 8]. Соотношение (4) может использоваться для уточнения фундаментальных физических констант и создания стандартов напряжения. На основе Д. э. совр. методами измерено отношение
Поиск по сайту: |


 (XIII.31)
(XIII.31) (XII.33)
(XII.33) ,
, — приведённая постоянная Планка, kB — постоянная Больцмана, μ0 — энергия уровня Ферми, T — температура.
— приведённая постоянная Планка, kB — постоянная Больцмана, μ0 — энергия уровня Ферми, T — температура. ,
, — теплоёмкость кристаллической решётки.
— теплоёмкость кристаллической решётки. (238.1)
(238.1)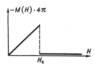 Кривая намагничивания сверхпроводников 1-го рода
Кривая намагничивания сверхпроводников 1-го рода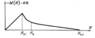 Кривая намагничивания сверхпроводников 2-го рода
Кривая намагничивания сверхпроводников 2-го рода Фазовая диаграмма для сверхпроводников
Фазовая диаграмма для сверхпроводников Скачок теплоёмкости сверхпроводника
Скачок теплоёмкости сверхпроводника , (2)
, (2) и
и  Т. о., проникновение магнитного поля в сверхпроводник 2-го рода начинается уже в поле, меньшем, чем Нк, когда условие равновесия (1) ещё нарушено в пользу сверхпроводящего состояния. Понять это парадоксальное на первый взгляд явление можно, если принять во внимание поверхностную энергию границы раздела нормальной и сверхпроводящей фаз. В случае сверхпроводников 1-го рода эта энергия положительна, так что появление границы раздела приводит к проигрышу в энергии. Это существенно ограничивает степень расслоения в промежуточном состоянии. Аномальные магнитные свойства сверхпроводников 2-го рода можно качественно объяснить, если принять, что в этом случае поверхностная энергия отрицательна. Именно к такому выводу приводит современная теория сверхпроводимости. При отрицательной поверхностной энергии уже при Н < Нк энергетически выгодным является образование тонких областей нормальной фазы, ориентированных вдоль магнитного поля. Возможность реализации такого состояния сверхпроводника 2-го рода была предсказана А. А. Абрикосовым (1952) на основе теории сверхпроводимости В. Л. Гинзбурга и Л. Д. Ландау. Позднее им же был произведён детальный расчёт структуры этого состояния. Оказалось, что нормальные области зарождаются в форме нитей, пронизывающих образец и имеющих толщину, грубо говоря, сравнимую с глубиной проникновения магнитного поля. При увеличении внешнего поля концентрация нитей возрастает, что и приводит к постепенному уменьшению магнитного момента. Т. о., в интервале значений поля от
Т. о., проникновение магнитного поля в сверхпроводник 2-го рода начинается уже в поле, меньшем, чем Нк, когда условие равновесия (1) ещё нарушено в пользу сверхпроводящего состояния. Понять это парадоксальное на первый взгляд явление можно, если принять во внимание поверхностную энергию границы раздела нормальной и сверхпроводящей фаз. В случае сверхпроводников 1-го рода эта энергия положительна, так что появление границы раздела приводит к проигрышу в энергии. Это существенно ограничивает степень расслоения в промежуточном состоянии. Аномальные магнитные свойства сверхпроводников 2-го рода можно качественно объяснить, если принять, что в этом случае поверхностная энергия отрицательна. Именно к такому выводу приводит современная теория сверхпроводимости. При отрицательной поверхностной энергии уже при Н < Нк энергетически выгодным является образование тонких областей нормальной фазы, ориентированных вдоль магнитного поля. Возможность реализации такого состояния сверхпроводника 2-го рода была предсказана А. А. Абрикосовым (1952) на основе теории сверхпроводимости В. Л. Гинзбурга и Л. Д. Ландау. Позднее им же был произведён детальный расчёт структуры этого состояния. Оказалось, что нормальные области зарождаются в форме нитей, пронизывающих образец и имеющих толщину, грубо говоря, сравнимую с глубиной проникновения магнитного поля. При увеличении внешнего поля концентрация нитей возрастает, что и приводит к постепенному уменьшению магнитного момента. Т. о., в интервале значений поля от  ,
, - фазы волновой ф-ции в сверхпроводниках по обe стороны от прослойки. При этом ток через контакт равен
- фазы волновой ф-ции в сверхпроводниках по обe стороны от прослойки. При этом ток через контакт равен



 , связанной с изменением энергии соотношением (3). T. о., при нестационарном Д. э. контакт, находящийся при пост. напряжении, генерирует перем. сверхпроводящий ток. Имеет место и обратный процесс: при облучении джозефсоновского контакта СВЧ-излучением с частотой
, связанной с изменением энергии соотношением (3). T. о., при нестационарном Д. э. контакт, находящийся при пост. напряжении, генерирует перем. сверхпроводящий ток. Имеет место и обратный процесс: при облучении джозефсоновского контакта СВЧ-излучением с частотой  , удовлетворяющей условию
, удовлетворяющей условию
 =4,83594000*1014 Гц/В с погрешностью 2*10-8, что позволяет создать стандарт вольта с погрешностью ~10-9.
=4,83594000*1014 Гц/В с погрешностью 2*10-8, что позволяет создать стандарт вольта с погрешностью ~10-9.