 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Функция распределения Ферми-ДиракаСтр 1 из 14Следующая ⇒
Понятие о квантовой статистике Ферми-Дирака Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень. Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам в металле. В статистике Ферми — Дирака среднее число частиц в состоянии с энергией εi есть
где ni — среднее число частиц в состоянии i, εi — энергия состояния i, gi — кратность вырождения состояния i (число состояний с энергией εi), μ — химический потенциал (который равен энергии Ферми EF при абсолютном нуле температуры), k — постоянная Больцмана, T — абсолютная температура. В (идеальном) ферми-газе в пределе низких температур μ = EF. В этом случае (полагая уровни энергии невырожденными gi = 1), функция распределения частиц называется функцией Ферми:
Распределение Ферми — Дирака как функция температуры. Заполнение уровней с энергиями Применение Статистики Ферми — Дирака и Бозе — Эйнштейна применяются в том случае, когда необходимо учитывать квантовые эффекты, когда частицы обладают «неразличимостью». Квантовые эффекты проявляются тогда, когда концентрация частиц Квантовая концентрация — это концентрация, при которой расстояние между частицами соразмерно с длиной волны де Бройля, то есть когда волновые функции частиц соприкасаются, но не перекрываются. Квантовая концентрация зависит от температуры. Статистика Ферми — Дирака (Ф — Д) применяется к фермионам (частицы, на которые действует принцип Паули), статистика Бозе — Эйнштейна (Б — Э) применяется к бозонам. Оба этих распределения становятся распределением Максвелла — Больцмана при высоких температурах и низких концентрациях. Распределением Максвелла — Больцмана часто описываются классические «различимые» частицы. Другими словами, конфигурация частицы A в состоянии 1 и частицы B в состоянии 2 отличается от конфигурации частицы B в состоянии 1 и частицы A в состоянии 2. Когда эта идея была проработана полностью, оказалось, что распределение частиц по энергетическим состояниям приводит к нефизическим результатам для энтропии, что известно, как парадокс Гиббса. Эта проблема исчезла, когда стал ясен тот факт, что все частицы неразличимы. И Ф — Д, и Б — Э приближаются к статистике Максвелла — Больцмана в пределе высоких температур и низких плотностей. Статистика Максвелла — Больцмана хорошо описывает поведение газов. Ф — Д часто используется для описания электронов в твердых телах, на ней, к примеру, базируются основные положения теории полупроводников в частности и электроники в целом. Вывод распределения
Распределение Ферми — Дирака как функция от Рассмотрим состояние частицы в системе, состоящей из множества частиц. Энергия такой частицы равна ε. Например, если наша система — это некий квантовый газ в «ящике», то подобное состояние может описываться частной волновой функцией. Известно, что для большого канонического ансамбля, функция распределения имеет вид
где E(s) — энергия состояния s, N(s) — число частиц, находящихся в состоянии s, μ — химический потенциал, s — это индекс, пробегающий все возможные микросостояния системы. В данном контексте, система имеет фиксированные состояния. Итак, если какое либо состояние занято n частицами, то энергия системы — Для фермионов, каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся s1 и s2 соответственно. Видно, что E(s1) = ε, N(s1) = 1, и E(s2) = 0, N(s2) = 0. Поэтому функция распределения принимает вид:
Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии sα вычисляется по формуле
Наличие состояния, занятого частицей, означает, что система находится в микросостоянии s1, вероятность которого
Обратите внимание, что энергетический уровень ε имеет вырождение gε. Теперь можно произвести простую модификацию:
Это число — ожидаемое число частиц, в суммарном состоянии с энергией ε. Для всех температур T, В пределе Влияние температуры Необходимо заметить, что химический потенциал зависит от температуры. Однако для систем, имеющих температуру ниже температуры Ферми
Поиск по сайту: |




 растёт с увеличением температуры.
растёт с увеличением температуры. (где nq — квантовая концентрация).
(где nq — квантовая концентрация).
 . Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергетические состояния более вероятны.
. Высокоэнергетические состояния имеют меньшую вероятность. Или, низкоэнергетические состояния более вероятны.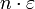 . Если состояние свободно, то энергия имеет значение 0. Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и то же физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.
. Если состояние свободно, то энергия имеет значение 0. Будем рассматривать равновесные одночастичные состояния как резервуар. После того, как система и резервуар займут одно и то же физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.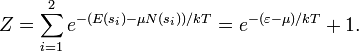


 называется распределением Ферми — Дирака. Для фиксированной температуры T,
называется распределением Ферми — Дирака. Для фиксированной температуры T, 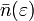 есть вероятность того, что состояние с энергией ε будет занято фермионом. Обратите внимание, что
есть вероятность того, что состояние с энергией ε будет занято фермионом. Обратите внимание, что 
 . Это означает, что состояния с энергией μ всегда будут иметь одинаковую вероятность быть заполненными или свободными.
. Это означает, что состояния с энергией μ всегда будут иметь одинаковую вероятность быть заполненными или свободными.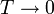 ,
,  , что часто используется, как аппроксимация
, что часто используется, как аппроксимация  . В реальности же:
. В реальности же: