 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры решения типовых задач
Пример 1. Как изменится начальная скорость простой реакции образования NOСl2 2NO(г)+ Cl2(г) = 2NOCl2(г), если уменьшить объем газовой смеси в 2 раза? Решение. Скорость данной реакции равна
Если обозначить концентрации NO и Cl2 до изменения объема, соответственно, через a и b, тогда В результате уменьшения объема в 2 раза концентрации NO и Cl2 увеличиваются в 2 раза, и скорость реакции станет равна
Тогда Пример 2. Скорость разложениявещества А описывается кинетическим уравнением первого порядка. Определить концентрацию вещества А через 100 с после начала реакции, если известно, что начальная концентрация его составляла 0,01 моль/л, а константа скорости равна 0,023 с-1. Решение. Используя интегральное кинетическое уравнение реакции первого порядка (2.9), имеем ln[A]t = ln[A]0 – kt; ln[A]t = ln0,01 – 0,023 ×100; ln[A]t = – 6,9; [A]t =0,001 моль/л.
Пример 3. Определить, за какое время израсходуется 90% исходного вещества, если известно, что скорость реакции описывается кинетическим уравнением первого порядка, а константа скорости равна 4,6 × 10-2 с-1. Решение. Если вещества А было 100%, израсходовано 90% (конверсия вещества), то к времени t останется 10% вещества. Подставляя эти значения в уравнение (2.9), найдем ln[A]t = ln[A]0 – kt, ln10 = ln100 – 4,6 × 10-2 ×t t = 50 с.
Пример 4. Известно, что скорость разложения вещества А описывается кинетическим уравнением первого порядка. Определить концентрацию вещества через 100 с после начала реакции, если известно, что исходная концентрация его была 0,4 моль/л, а время полупревращения Решение. Для нахождения константы скорости реакции воспользуемся уравнением (2.12)
откуда
Тогда концентрация через 100 с после начала реакции ln[A]t = ln[A]0 – kt; ln[A]t = ln 0,4 – 0,0231.100 = – 0,916 – 2,31 = – 3,226 [A]t = е - 3,226 = 0,0397 моль/л.
Пример 5. Для некоторой реакции n А + m В ® продукты, проводимой при различных исходных концентрациях реагирующих веществ, экспериментально определяли скорость реакции: сначала при различных концентрациях вещества В и фиксированной концентрации вещества А (опыты 1-3), затем при различных начальных концентрациях А и постоянной концентрации В (опыты 4-6). Полученные данные представлены в табл. 1. Таблица 1
Определить вид дифференциального кинетического уравнения и константу скорости реакции. Решение. Зависимость начальной скорости от концентрации для данной реакции выражается дифференциальным кинетическим уравнением
Прологарифмируем это выражение
Величины k, n и m для рассматриваемой реакции (при Т= const) являются постоянными и не зависят от концентрации реагентов. Так как в трех опытах (1-3) концентрация вещества А постоянна (обозначим ее [A]0), то в уравнении сумма (lnk + nln[A]0) будет тоже величиной постоянной. Обозначим ее lnk + nln[A]0 = D1. Тогда уравнение можно переписать так: ln Зависимость представляет собой в координатах ln[B] — ln В табл. 2 представлены значения логарифмов концентраций и скоростей для опытов (1-6). Таблица 2
По результатам опытов (1-3) построим график зависимости ln
Рис. 13. Определение порядка реакции по веществу В В последующих опытах (4-6) концентрация вещества B остается постоянной ([B]= [B]0), поэтому lnk + mln[B]0 = D2 ln По результатам опытов (4-6) построим график зависимости ln
Рис.14. Определение порядка реакции по веществу А Таким образом, зависимость скорости от концентрации для исследуемой реакции
В этом уравнении порядок реакции по веществу B равен 2, а порядок реакции по веществу A равен 1. Сумма порядков по реагирующим веществам, равная 3, дает общий порядок реакции. Для определения константы скорости прологарифмируем дифференциальное кинетическое уравнение с учетом полученных порядков реакции по веществам A и B lnk = ln Вычислив константу скорости реакции для каждого опыта (в табл. 3 представлены данные для трех опытов), найдем среднее значение константы
Таблица 3
Таким образом, дифференциальное кинетическое уравнение имеет вид
Пример 6. Определить энергию активации Еа реакции, для которой при повышении температуры от 22 до 32 °C константа скорости возрастает в 2 раза. Решение. Запишем уравнение Аррениуса для двух температур в виде
В результате вычитания первого уравнения из второго, получим
следовательно,
Отношение k2 /k1= 2 по условию. Переводим температуру в Кельвины и подставляем значения в уравнение
Пример 7. Энергия активации некоторой реакции при отсутствии катализатора равна 75 кДж/моль, а с катализатором 50 кДж/моль. Во сколько раз возрастет скорость реакции в присутствии катализатора, если реакция протекает при 25°C? Решение. Обозначим энергию активации реакции без катализатора через
В результате вычитания первого уравнения из второго
Подставляя в последнее уравнение данные задачи, выражая энергию активации в Джоулях и учитывая, что Т= 298 К, получим
Таким образом, в присутствии катализатора скорость реакции возрастет в 24 тысячи раз.
Пример 8. Приведенные ниже данные соответствуют температурной зависимости константы скорости реакции, имеющей первый порядок
Определите энергию активации и значение предэкспоненциального множителя. Рассчитайте константу скорости при температуре T=303 K. Решение. Согласно уравнению Аррениуса зависимость константы скорости от температуры имеет вид
поэтому необходимо построить график зависимости
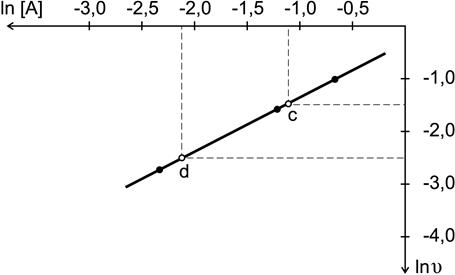
Рис.15. Определение энергии активации
Энергию активации можно определить из тангенса угла наклона прямой (рис. 15)
Определим значения предэкспоненциального множителя. Для произвольной точки на прямой зависимости Подставляем значения
откуда
Подставляя найденные значения энергии активации и предэкспоненциального множителя в уравнение Аррениуса, получим зависимость константы скорости от температуры
Найдем значение константы скорости при температуре Т=303К
или по уравнению
Можно определить константу скорости и непосредственно из графика (рис.15). Отложив на оси Пример 9. Константа равновесия реакции А + В « C + D равна единице. Исходные концентрации: [А]0 = 0,01моль/л, [В]0 =0,03 моль/л. Определить равновесные концентрации всех четырех веществ. Решение. 1. Пишем уравнение реакции. 2. Для каждого из участников реакции записываем начальные концентрации исходных веществ (в моль/л). Т.к. начальные концентрации продуктов реакции не оговариваются в условии задачи, то принимаем их равными нулю. 3. По уравнению реакции определяем изменение концентраций всех веществ к моменту достижения равновесия. Из уравнения реакции видно, что из каждого моля А и В образуется по одному молю С и D. Принимаем, что в ходе реакции к моменту достижения равновесия прореагировало x моль/л вещества А. Если прореагирует х молей А, то должно прореагировать также х молей В, в то же время должно образоваться по х молей С и D. 5. Определяем равновесные концентрации веществ. При протекании реакции в прямом направлении до состояния равновесия происходит уменьшение концентраций исходных веществ и увеличение концентраций продуктов реакции. А + В « С + D Начальное состояние 0,01 0,03 0 0
Число молей по уравнению 1 1 1 1
Изменение концентраций x x x x
Равновесное состояние 0,01 – x 0,03 – x x x
6. Пишем выражение закона действующих масс. Подставляем в него найденные значения равновесных концентраций.
7. Решаем уравнение. При этом учитываем, что отрицательный корень не имеет физического смысла, и убыль концентрации исходного вещества не может быть больше величины самой концентрации. х = 0,0075 моль/л. 8. Находим равновесные концентрации. [А] = [А]0 – x = 0,01 – 0,0075 = 0,0025 моль/л; [B] = [B]0 – x = 0,03 – 0,0075 = 0,0225 моль/л; [C] = x = 0,0075 моль/л; [D] = x = 0,0075 моль/л. Пример 10. В системе А(г) + В(г) « 2С(г) равновесные концентрации равны: [А] =0,018 моль/л, [В] = 0,011 моль/л, [С] = 0,016 моль/л. Найти константу равновесия реакции и исходные концентрации веществ А и В. Решение. Константа равновесия данной реакции выражается уравнением
Для нахождения исходных концентраций веществ А и В учтем, что, согласно уравнению реакции, из 1 моля А и 1 моля В образуется 2 моля С. Поскольку по условию задачи в каждом литре системы образовывалось 0,016 моля вещества С, то при этом было израсходовано 0,008 моля вещества А и 0,008 моля вещества В. А + В « 2 С Начальное состояние ? ?
Число молей по уравнению 1 1 2
Изменение концентраций 0,008 0,008 0,016
Равновесное состояние 0,018 0,011 0,016
Таким образом, исходные концентрации равны: [А]0 = 0,018 + 0,008 = 0,026 моль/л; [В]0 =0,011 + 0,008 = 0,019 моль/л.
Пример 11. Химическое равновесие гомогенной реакции A + B « 2D, протекающей при T = const, установилось при следующих концентрацияхреагирующих веществ: [А] = 0,4 моль/л; [В] = 0,2 моль/л; [D] =0,4 моль/л. Затем концентрацию вещества B увеличили до 0,5 моль/л. Рассчитайте новые равновесные концентрации реагирующих веществ. Решение. Вычислим константу равновесия данной реакции:
После добавления вещества B возникло новое состояние системы с концентрациями [А]=0,4 моль/л; [В] = 0,5 моль/л; [D] = 0,4 моль/л. В соответствии с принципом Ле Шателье при увеличении концентрации [В] равновесие сместится в сторону прямой реакции. Движение системы к новому состоянию равновесия должно сопровождаться увеличением концентрации D и снижением концентрации A и B. Если концентрация вещества A снизится на x моль/л, то в соответствии с уравнением реакции концентрация вещества B должна уменьшиться на такую же величину и концентрация вещества D –увеличиться на 2x моль/л. Тогда равновесные концентрации будут равны: [А] = 0,4 – x; [В] = 0,5 – x; [D] = 0,4 + 2 x. Реакция протекает при постоянной температуре, следовательно, константа равновесия
Откуда x = 0,07.
А + В « 2D
Начальное равновесное состояние 0,4 0,2 0,4
Состояние системы после добавления вещества B 0,4 0,5 0,4
Число молей по уравнению 1 1 2
Изменение концентраций x x 2x
Новое равновесное состояние 0,4 – x 0,5 – x 0,4 + 2x
Новые равновесные концентрации: [А] = 0,4 – x = 0,4 – 0,07 = 0,33 моль/л; [В] = 0,5 – x = 0,5 – 0,07 = 0,43 моль/л; [D] = 0,4 + 2 x = 0,4 + 0,14 = 0,54 моль/л.
Если в качестве проверки подставить значения новых равновесных концентраций в выражение константы равновесия, получим
Пример 12. Эндотермическая реакция разложения пентахлорида фосфора протекает по уравнению
PCl5 (г) « PCl3 (г) + Cl2 (г); DН = +92,59 кДж.
Как надо изменить: а) температуру; б) давление; в) концентрации реагирующих веществ, чтобы сместить равновесие в сторону прямой реакции – разложения PCl5? Решение. В соответствии с принципом Ле Шателье, если на систему, находящуюся в состоянии равновесия, оказать внешнее воздействие, то смещение равновесия происходит в сторону той реакции (прямой или обратной), которая ослабляет эффект внешнего воздействия. 1. Смещение равновесия при изменении температуры связано с тепловым эффектом реакции. Так как рассматриваемая реакция эндотермическая (DН > 0), то для смещения равновесия в сторону прямой реакции нужно повысить температуру. 2. Так как в данной реакции разложение PCl5 ведет к увеличению объёма (из одного моля газа образуются два), то для смещения равновесия в сторону прямой реакции надо уменьшить давление. 3. Чтобы сместить равновесие в сторону прямой реакции, необходимо увеличить концентрацию PCl5.
Поиск по сайту: |
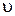 =k [NO]2[Cl2 ].
=k [NO]2[Cl2 ].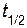 равно 30 с.
равно 30 с. ,
, .
.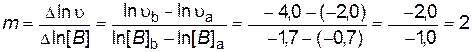 .
.
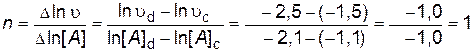 .
.
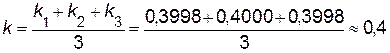 л²· моль-2·с-1.
л²· моль-2·с-1.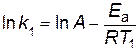 ,
,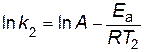 .
.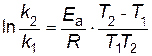 ,
,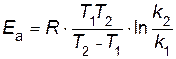 .
. .
. , а с катализатором – через
, а с катализатором – через  ; соответствующие константы скорости реакции обозначим через
; соответствующие константы скорости реакции обозначим через 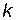 и
и  . Предположим, что величина А для данной реакции постоянна и не зависит от присутствия катализатора. Используя уравнение Аррениуса, находим
. Предположим, что величина А для данной реакции постоянна и не зависит от присутствия катализатора. Используя уравнение Аррениуса, находим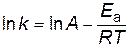 ,
,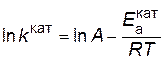 .
.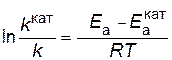 .
.
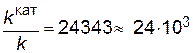 .
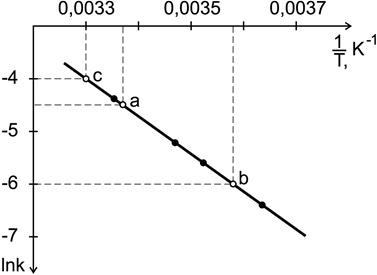
.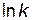 от
от 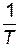 .
.
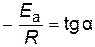 ;
;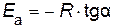 ;
; ;
;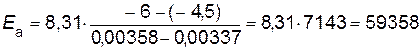 Дж/моль.
Дж/моль.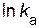 = – 4,5;
= – 4,5;  ,
, 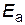 в уравнение Аррениуса
в уравнение Аррениуса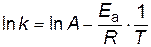 ,
, ,
,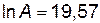 ;
; 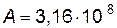 .
.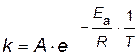 ;
;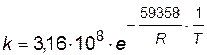 ;
; .
.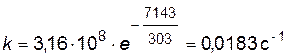
 ;
; ;
;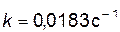 .
.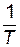 значение
значение  (точка c), находим по графику
(точка c), находим по графику 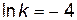 ;
; 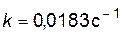 .
.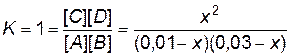 .
.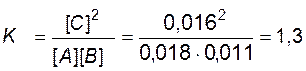 .
.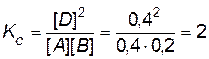 .
.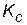 останется прежней, равной 2. Подставляем новые равновесные концентрации реагирующих веществ в выражение константы равновесия:
останется прежней, равной 2. Подставляем новые равновесные концентрации реагирующих веществ в выражение константы равновесия: .
.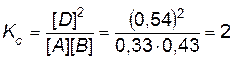 .
.