 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Первообразная функция, неопределённый интеграл и его свойства
К понятию первообразной функции приводят многие задачи математического анализа и физики. Рассмотрим былинный физический пример: известен закон изменения скорости тела Скорость – это производная от пройдённого пути: Общая же постановка вопроса такова: в распоряжении есть некоторая функция Определение: функция Например, для Простое, но требующее доказательства утверждение: Теорема: пусть Доказательство: поскольку производная константы равна нулю, то: Так, для функции Докажем обратное утверждение: любая другая первообразная Вот это уже менее очевидный факт. И в самом деле – вдруг для функции Пусть
Но с другой стороны, из дифференциального исчисления известно, что данному условию удовлетворяет функция-константа и только она: Откуда и следует равенство Вуаля: Определение: множество всех первообразных
Напоминаю, что функция Для нашего демонстрационного примера: Проверка: Любая ли функция интегрируема? Нет. Сформулируем достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём. Как видите, условие довольно-таки лояльное – для существования первообразнойдостаточно лишь непрерывности. Ниже по тексту, если не сказано иного, все функции будем считать интегрируемыми.
Поиск по сайту: |
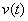 , требуется найти закон изменения координаты
, требуется найти закон изменения координаты 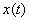 данного тела.
данного тела. (см. урок о смысле производной), таким образом, для решения задачи необходимо по заданной функции
(см. урок о смысле производной), таким образом, для решения задачи необходимо по заданной функции 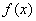 и возникает потребность выяснить, от какой функции она произошла. То есть, необходимо найти ТАКУЮ функцию
и возникает потребность выяснить, от какой функции она произошла. То есть, необходимо найти ТАКУЮ функцию  , чтобы
, чтобы  .
. из этого промежутка выполняется равенство
из этого промежутка выполняется равенство  (раскрывать дифференциал мы научились ещё на первом уроке онеопределённом интеграле).
(раскрывать дифференциал мы научились ещё на первом уроке онеопределённом интеграле). первообразной функцией на всей числовой прямой будет являться функция
первообразной функцией на всей числовой прямой будет являться функция  . И действительно, для любого «икс»:
. И действительно, для любого «икс»: .
. , где
, где 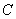 – произвольная константа, тоже будетпервообразной функцией для
– произвольная константа, тоже будетпервообразной функцией для  , следовательно,
, следовательно,  , где
, где  (мысленно поподставляйте конкретные числовые значения).
(мысленно поподставляйте конкретные числовые значения). для функции
для функции  .
. – это две первообразные для функции
– это две первообразные для функции  , или если записать короче:
, или если записать короче: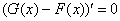


 . Таким образом, по определению:
. Таким образом, по определению: , где
, где  –подынтегральным выражением, а сам процесс отыскания множества первообразных
–подынтегральным выражением, а сам процесс отыскания множества первообразных  – интегрированием. Интегрирование – это восстановление функции
– интегрированием. Интегрирование – это восстановление функции  , где
, где  – исходная подынтегральная функция.
– исходная подынтегральная функция.