 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Динамические модели чувствительных элементов
Для определения динамических характеристик датчиков на их вход необходимо подавать переменные внешние сигналы и следить за реакцией на выходе. В общем виде, тестовые внешние сигналы могут быть любой формы, определяемой только практическими потребностями. Например, для определения собственной частоты акселерометра, лучшими тестовыми сигналами являются синусоидальные колебания переменной частоты, а для термисторного щупа тестовый сигнал должен представлять собой ступенчатую функцию температуры. Для других случаев чаще всего применяются ступенчатая или импульсная функции. Ступенчатые функции обладают теоретически бесконечным частотным спектром, что является причиной их использования для определения динамических характеристик датчиков, поскольку позволяют проводить тестирование одновременно на всех частотах. Математически поведение датчика может быть описано дифференциальным уравнением, порядок которого зависит от физической природы чувствительного элемента и конструкции всей системы. Существует несколько типов зависимостей между входным сигналом s и выходной реакцией S: нулевого порядка, первого порядка и второго порядка.
3.14. Динамические модели чувствительных элементов I Уравнение нулевого порядка является статическим или независящим от времени: S{i) = Gs{t), (3.148) где G — постоянная передаточная функция. Это выражение можно записать в нескольких видах (см. уравнения 2.1-2.4). Важным здесь является то, что Сне зависит от времени, поэтому выходной сигнал системы нулевого порядка на входную ступенчатую в ответ на ступенчатое входное воздействие будет также ступенчатым. Уравнение первого порядка имеет вид:
где а1 и а0 — константы. Это уравнение описывает поведение датчиков, сначала накапливающих энергию, а потом ее отдающих. Пример таких датчиков — датчик температуры, обладающий теплоемкостью и связанный с окружающей средой через тепловое сопротивление. Выходной сигнал такой системы в ответ на входную ступенчатую функцию носит экспоненциальный характер:
где S0 — статическая реакция датчика, а т - постоянная времени, характеризующая инерционность системы. Типичная реакция системы первого порядка показана на рис. 2.9Б во второй главе.
Перейдем к уравнениям второго порядка:
140 Глава 3. Физические приципы датчиков Критическое демпфирование системы (см. рис. 2.10 главы 2) соответствует коэффициенту затухания b = 1. При b > 1 наступает передемпфирование, а при b < 1 — недодемпфирование. Для получения более подробной информации о динамических характеристиках надо обратиться к специализированной литературе, например, [39]. Математическое моделирование датчика является мощным инструментом для прогнозирования его характеристик. Моделирование бывает двух типов: статическое и динамическое. Статические модели обычно используют передаточную функцию датчика в том виде, как она представлена во второй главе. В этой главе дано краткое описание способов оценки динамических характеристик системы. В состав динамических моделей могут входить несколько независимых переменных, одной из которых всегда является время. Рассматриваемые модели соответствуют представлению датчиков в виде систем с сосредоточенными параметрами. В этом разделе все математические модели строятся на применении законов физики к отдельным элементам системы. Другими словами, при разработке модели датчик разбивается на отдельные элементы, и каждый элемент рассматривается отдельно. После этого математические описания индивидуальных элементов объединяются в единую модель, описывающую поведение всей системы в целом. Механические элементы Динамический механический элемент можно представить в виде массы (инерционного компонента), соединенной с пружиной и демпфирующим устройством. При вязкостном демпфировании и прямолинейном перемещении удерживающая сила пропорциональна скорости движения. Аналогично этому и при круговом движении удерживающая сила всегда пропорциональна угловой скорости. Поэтому сила или крутящий момент, формируемые штоком или пружиной, как правило, также пропорциональны перемещению. В таблице 3.4 приведены основные уравнения для некоторых механических элементов. Таблица 3.4. Механические, тепловые и электрические аналогии
3 14 Динамические модели чувствительных элементов
можно применить второй закон Ньютона и вы- вести из него уравнение движения. Для прямолинейного движения и совмес Для вращательного движения закон Нью- тона гласит, что сумма моментов сил, действую- щих на тело, равна произведению его моментаинерции на угловое ускорение. Момент сил измеряется в Ньютонхмеф (Нхм), момент инерции в килофаммах на метр квадратный (кгм2), а угловое ускорение - в радианах на секунду в квадрате (рад/с2). Рассмотрим одноосевой акселерометр, состоящий из инерционного элемента, чье движение преобразуется в электрический сигнал. Для этого, например, можно применить пьезоэлектрический преобразователь. На рис. 3.49А показана механическая модель такого акселерометра. Масса М удерживается пружиной, обладающей коэффициентом жесткости к. Движение массы демпфируется успокоительным устройством, обеспечивающим коэффициент затухания b. Инерционный элемент может перемещаться в корпусе акселерометра только в горизонтальном направлении. Во время движения на устройство действует ускорение dx/dt2, а вькодной сигнал пропорционален отклонению массы на расстояние х0. Поскольку инерционный элемент может перемещаться только в одном направлении, акселерометр имеет только одну степень свободы. На рис. 3.49Б показана диаграмма сил, действующих на свободное тело массы М. Отметим, что х0 равно сумме смещения тела от равновесного состояния х и некоторого фиксированного расстояния. Применяя второй закон Ньютона, получаем следующее соотношение:
гдеf — ускорение инерционной массы с учетом ускорения свободного падения:
Глава 3. Физические приципы датчиков
Отметим, что каждый член в уравнении (3.156) имеет размерность ньютон (Н). Это выражение является дифференциальным уравнением второго порядка, что означает, что на выходе акселерометра могут появиться нежелательные колебания. На практике, регулируя коэффициент затухания Ь, добиваются состояния критического демпфирования. Тепловые элементы Тепловые элементы — это радиаторы, нагревательные элементы, теплоизолято-ры, отражатели и поглотители тепла. При изучении тепловых характеристик датчик рассматривается как составная часть измерительной системы, при этом учитываются: теплопередача через корпус устройства и монтажные элементы, конвекция воздуха, обмен тепловыми излучениями с остальными объектами и т.д.
Рис. 3.50.А — тепловая модель нагревательного элемента, Б — электрическая схема с резистивными, емкостными и индуктивными элементами
где С = М * е — теплоемкость тела (Дж/К), Т — температура (К), ΔQ — интенсивность теплового потока (Вт), М — масса тела (кг), а с — удельная теплоемкость материала (Дж/(кг*К). Интенсивность теплового потока, проходящего через тело, является функцией теплового сопротивления тела, которая на практике часто считается линейной: 3.14. Динамические модели чувствительных элементов 143
где R — тепловое сопротивление (К/Вт), а Т1-Тг — градиент температуры на элементе, теплопроводность которого рассматривается. Для иллюстрации этого проанализируем нагревательный элемент, имеющий температуру Th (рис.3.50А). Элемент покрыт слоем теплоизоляционного материала. Температура окружающей среды равна T0 Q1 — это тепло, приложенное к элементу, Q0 — тепловые потери. Из уравнения (3.157) следует, что
уравнения (3.158):
Объединив эти два выражения, получим дифференциальное уравнение:
Это уравнение первого порядка является типичным для тепловых систем. Тепловые элементы очень стабильны по своей природе, если только не входят в состав устройств с контуром обратной связи. Выходная реакция простого теплового элемента на ступенчатое внешнее воздействие характеризуется постоянной времени, равной произведению теплоемкости на тепловое сопротивление: τT= CR. Постоянная времени измеряется в секундах, и для пассивных охлаждающих элементов она равна времени, за которое выходной сигнал достигает уровня 37% от начального температурного градиента.
Поиск по сайту: |




 Такие дифференциальные уравнения соответствуют датчикам или системам, в состав которых входят по два энергонакопительных элемента — например, катушка индуктивности и конденсатор или датчик температуры и конденсатор. Поскольку в состав датчиков второго порядка часто входят элементы, совершающие колебательные движения, это может приводить к неустойчивости всей системы. На рис. 2.1 IE во второй главе показана типичная форма выходного сигнала устройства второго порядка в ответ на ступенчатую входную функцию. Динамическая ошибка в таких системах определяется несколькими факторами: частотой ω0 и коэффициентом затухания b, связанных с независимыми коэффициентами уравнения (3.151) следующими соотношениями:
Такие дифференциальные уравнения соответствуют датчикам или системам, в состав которых входят по два энергонакопительных элемента — например, катушка индуктивности и конденсатор или датчик температуры и конденсатор. Поскольку в состав датчиков второго порядка часто входят элементы, совершающие колебательные движения, это может приводить к неустойчивости всей системы. На рис. 2.1 IE во второй главе показана типичная форма выходного сигнала устройства второго порядка в ответ на ступенчатую входную функцию. Динамическая ошибка в таких системах определяется несколькими факторами: частотой ω0 и коэффициентом затухания b, связанных с независимыми коэффициентами уравнения (3.151) следующими соотношениями:


 Самый простой способ вывода уравнений движения - вьщеление каждого инерционного элемента (массы) и рассмотрение его как свободного тела. При этом предполагается, что все свободные компоненты начинают свое движение из положения равновесия, а удерживающие силы или моменты, возникающие при перемещении, возвращают их снова на исходную позицию. При выполнении этих условий к каждому элементу
Самый простой способ вывода уравнений движения - вьщеление каждого инерционного элемента (массы) и рассмотрение его как свободного тела. При этом предполагается, что все свободные компоненты начинают свое движение из положения равновесия, а удерживающие силы или моменты, возникающие при перемещении, возвращают их снова на исходную позицию. При выполнении этих условий к каждому элементу


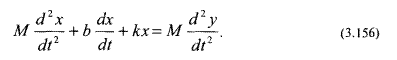 Подставив это выражение в уравнение (3.154), получим требуемое уравнение движения:
Подставив это выражение в уравнение (3.154), получим требуемое уравнение движения:
 Вспомним, что тепло передается тремя способами: через теплопроводность, естественную и принудительную конвекцию и тепловое излучение (раздел 3.12). При построении простой модели с сосредоточенными параметрами для определения изменения температуры объекта можно воспользоваться первым законом термодинамики, по которому скорость изменения внутренней энергии тела равна разности втекающего и вытекающего потоков тепла, что очень напоминает задачу об уровне воды в резервуаре, когда в одну трубу вода заливается, а из другой сливается. Тогда тепловой баланс можно выразить в виде уравнения:
Вспомним, что тепло передается тремя способами: через теплопроводность, естественную и принудительную конвекцию и тепловое излучение (раздел 3.12). При построении простой модели с сосредоточенными параметрами для определения изменения температуры объекта можно воспользоваться первым законом термодинамики, по которому скорость изменения внутренней энергии тела равна разности втекающего и вытекающего потоков тепла, что очень напоминает задачу об уровне воды в резервуаре, когда в одну трубу вода заливается, а из другой сливается. Тогда тепловой баланс можно выразить в виде уравнения:
 а
а
