 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Влияние ионной силы на скорость реакции
Уравнение Аррениуса справедливо и для реакций в растворах. В этом уравнении и во всех уравнениях химической кинетики фигурируют концентрации реагирующих веществ. В термодинамике же константа равновесия неидеальной системы выражается через активности. Это обстоятельство необходимо учитывать, если в кинетическое уравнение входит константа равновесия. Правда, при реакциях в газовой фазе и между нейтральными молекулами в растворе в этом нет практической необходимости, но при рассмотрении реакций между заряженными частицами подобное пренебрежение может явиться источником существенных ошибок. Для константы скорости бимолекулярной реакции
протекающей в растворе, теория активного комплекса дает
И, комбинируя эти уравнения, получаем Это уравнение Бренстеда-Бьеррума. Оно справедливо для константы скорости реакции, протекающей в любой неидеальной среде. Величина k0 имеет смысл константы скорости при бесконечном разведении, т. е. при γ=1.
Для использования уравнения в конкретном случае необходимо задаться тем или другим аналитическим выражением для коэффициентов активности. Если в качестве стандартного состояния выбрать бесконечное разведение, теория электролитов дает следующее приближенное соотношение для коэффициента активности: Рассмотрим два случая: 1. Взаимодействие между заряженными частицами.
Для случая взаимодействия между двумя ионами второй сомножитель мал, и тогда Следовательно, логарифм константы скорости, согласно теории, должен быть линейной функцией корня квадратного из ионной силы, а тангенс угла наклона прямой определяется соотношением зарядов реагирующих частиц. 2. Взаимодействие между ионом и нейтральной молекулой: z = 0. Согласно уравнению, коэффициент активности для нейтральной молекулы: γ=eβI
Малость величины β позволяет разложить экспоненту в ряд, пренебрегая членами высших степеней для не очень больших значений I: Следовательно, константа скорости пропорциональна ионной силе. При рассмотрении р-ций в растворах следует учитывать, что, хотя число столкновений реагирующих частиц с растворителем очень много, эти столкновения увеличивают как скорость активации, так и скорость дезактивации. Поэтому в целом скорость реакции меняется мало – увеличивается или уменьшается до двух раз. НО есть исключения: типичный случай – реакция Меншуткина: R-X (Х – галоген) + N - (Ri)3 = X – N – (Ri)4 . Скорость этой реакции сильно зависит от растворителя. Очень малая часть соударений приводит к реакции – стерический множитель от 10-5 до 10-8. Причины – необходима специфическая ориентация при столкновении, имеется специфическое распределение энергии по внутренним степеням свободы.
Поиск по сайту: |
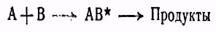
Термодинамическая же константа равновесия между исходными веществами и активным комплексом
