|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Влияние температуры на константу равновесия
При рассмотрении вопроса о смещении равновесия показано качественное влияние температуры на константу равновесия. Количественно эта зависимость определяется уравнением Вант-Гоффа. Покажем вывод этого уравнения. Так как константа скорости химической реакции зависит только от температуры, то, очевидно, и константа равновесия зависит только от температуры. Подставив в выражение константы равновесия значения констант скоростей прямой и обратной реакций из уравнения Аррениуса и выполнив несложные преобразования, можно получить
Кр = k1/k2 = (А1/А2)е-(Е2-Е1)/RT = А е-DЕ/RT, (2.13)
где А1 и А2, Е1 и Е2-соответственно предэкспоненциальные множители и энергии активации прямой и обратной реакций, а DЕ - разность энергий активации обратной и прямой реакций. Эта разница соответствует тепловому эффекту реакции. Тогда зависимость константы равновесия от температуры выразится уравнением:
Кр = А еQ/RT (2.14)
Если Q < 0, т.е. реакция идет с поглощением тепла (эндотермическая), то значение константы равновесия с повышением температуры возрастает (рис.20). Если Q > 0, т.е. тепло в результате реакции выделяется (экзотермическая), то с увеличением температуры значение константы уменьшается.
Рис.20. Зависимость константы равновесия от температуры
Выводы, сделанные на основании уравнения Вант-Гоффа, находятся в полном соответствии с принципом Ле-Шателье. Покажем возможности использования уравнения Вант-Гоффа для определения константы равновесия при разных температурах и вычисления теплового эффекта реакции. Прологарифмируем уравнение (2.14):
lgКр = Q/(2,303 RT) + lgA или lgКр = (Q/(2,303 R))(1/Т) + lgA (2.15)
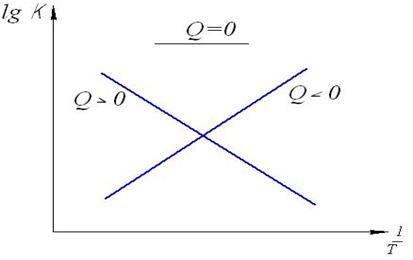
Последнее выражение представляет собой уравнение прямой линии в координатах lgКр – 1/Т: Если построить график зависимости lgКр от 1/Т (рис.21), то полученная экспериментальная прямая отсечет на оси ординат отрезок, равный lgA и имеющий наклон, равный Q/(2,303RT), откуда можно определить Q. Если принять, что тепловой эффект реакции не зависит от температуры, что допустимо в небольших температурных интервалах, то зная константу равновесия при одной температуре (Т1), можно определить константу равновесия при любой другой температуре (Т2). Запишем выражения константы равновесия для температур Т1 иТ2:
lgКр1 = Q/(2,303RT1) + lgA, lgКр2 = Q/(2,303RТ2) + lgA.
Рис.21. Зависимость логарифма константы равновесия от температуры.
Вычитая второе уравнение из первого, получим:
lg(Кр1/Кр2) = (Q/(2,303R)) (1/Т1-1/Т2) (2.16).
Этим уравнением можно воспользоваться для вычисления теплового эффекта реакции, если известны константы равновесия при двух температурах. Немаловажно отметить, что константа равновесия (а значит и состояние равновесия) не зависит от энергии активации. Это следует из уравнения (2.13) и подтверждается экспериментально. Очевидно, что изменение, например, увеличение константы равновесия с изменением температуры еще не означает достижения высокого выхода продуктов реакции и, соответственно, целесообразности осуществления процесса в препаративных целях, так как абсолютное значение Кр может оставаться невысоким. Например, уже при достаточно высокой температуре 1000 К константа равновесия эндотермической реакции
N2 + O2 « 2NO
очень мала - всего 5,5.10-9. Повышение температуры до 2000 К увеличивает значение константы до 3,3.10-4, но даже при 5000 К ее величина составляет всего 0,24. Только при температуре 15000 К значение константы равновесия образования оксида азота достигает 4,5 - величины, которую в какой-то степени можно считать приемлемой. Но эта температура в два с половиной раза выше, чем на поверхности Солнца.
Поиск по сайту: |