 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Влияние температуры на скорость реакции
Согласно молекулярно-кинетической теории, число соударений молекул пропорционально Зависимость скорости реакции от температуры приближённо описывается эмпирическим законом Вант-Гоффа: при повышении температуры на каждые 10 градусов скорость большинства химических реакций возрастает в 2- -4 раза.
Математическое выражение этой закономерности:
vt = v0 gn или kt = k0 gn
где v0 (или k0) – скорость реакции при температуре to; vt (или kt) – скорость реакции при температуре t1; γ – температурный коэффициент скорости реакции;
Температурный коэффициент показывает, как увеличится скорость реакции при повышении температуры на 10 градусов; он имеет свое значение для каждой конкретной реакции, т. к. зависит от природы реагирующих веществ. Определив экспериментально величину γ (или воспользовавшись справочными данными) можно приближённо рассчитать значение скорости при любой температуре (в относительно небольшом температурном интервале). Более строго зависимость скорости от температуры описывается уравнением Аррениуса (см. п.1.3.4). Большое влияние температуры на скорость реакций находит своё объяснение в теории активации. С ростом температуры средняя энергия молекул системы возрастает. На рис.10 кривые, относящиеся к температурам T2 и T3, смещены вправо – в сторону более высоких энергий по сравнению с кривой, относящейся к температуре Т1; соответственно, увеличивается и доля молекул, обладающих энергией, превышающей энергию активации реакции, следовательно, число активных молекул, а значит и эффективных столкновений, также увеличивается, поэтому скорость реакции растёт:
v(T1) < v(T2) < v(T3)
Рис.10. Распределение молекул по энергии при различных температурах: Еср-средняя энергия молекул; Еа-энергия активации; ∆N/(N∆E)-доля молекул с определенной энергией. Уравнение Аррениуса
Это уравнение, предложенное шведским учёным Аррениусом в 1889 году, выражает одновременно зависимость скорости реакции от энергии активации, температуры, а также энтропии активации реакции:
Входящие в это уравнение величины k, Ea, T, R определены ранее. Величина H2 + I2 ® 2HI
а) б) Рис 11. Благоприятные (а) и неблагоприятные (б) столкновения молекул H2 и I2
Другим примером роли стерического фактора может служить уменьшение скорости реакции этерификации (спирт + кислота ® сложный эфир + вода) при переходе от первичных спиртов к третичным. Третичные спирты (R3C-OH) имеют более сложное пространственное строение, чем первичные (RСН2–OH), поэтому возможность их благоприятной ориентации по отношению к молекулам кислоты менее вероятна. Величина ΔSa называется энтропией активации(Дж/моль·К), она пропорциональна отношению числа благоприятных способов ориентации к их общему возможному числу:
Отсюда очевидно, что чем жёстче требования ориентации, тем меньше будет величина ΔSa, а значит и скорость реакции. Значение стерического фактора особенно сказывается на реакциях с участием сложных молекул с разветвлённой структурой. Z – множитель, отражающий общее число столкновений взаимодействующих частиц. Произведение
Определение энергии активации.Прологарифмировав уравнение Аррениуса, получим:
Если построить график зависимости экспериментальных величин lgk от
Рис.12. Графический расчет энергии активации
Следовательно, для определения энергии активации необходимо иметь опытные данные по значениям константы скорости при нескольких температурах. Их представляют в виде таблицы:
и строят график зависимости Если известны только два значения константы скорости k1 и k2 при Т1 и Т2 соответственно, то уравнение (1.22) для этого случая запишется следующим образом:
Вычитая уравнение (1.24) из (1.23), получим:
или
Еа = 2,3RT1T2.lg(k2/k1)/(T2-T1) (1.25)
Уравнение Аррениуса, таким образом, математически выражает важнейшие положения, вытекающие из теории активных столкновений: 1) чем больше концентрация реагирующих веществ, тем выше скорость реакции (тем больше число столкновений); 2) чем больше энергия активации реакции, тем её скорость меньше (тем меньше доля активных молекул); 3) повышение температуры увеличивает скорость реакции (увеличивается доля активных молекул); 4) чем выше энергия активации, тем быстрее увеличивается скорость реакции с ростом температуры (быстрее увеличивается доля молекул с большими энергиями); 5) чем проще строение молекул, тем выше скорость реакции (тем больше доля благоприятных взаимных ориентаций молекул в пространстве).
Поиск по сайту: |
 , поэтому при увеличении температуры на 10о скорость реакции должна возрастать на 1-2%. Однако, в действительности скорость реакций гораздо более чувствительна к изменению температуры. Так, если осуществить синтез воды при 20оС даже на 15% практически невозможно (на это потребовалось бы 54 миллиарда лет), то при 500оС для этого необходимо всего 50 минут, а при 700оС реакция происходит мгновенно.
, поэтому при увеличении температуры на 10о скорость реакции должна возрастать на 1-2%. Однако, в действительности скорость реакций гораздо более чувствительна к изменению температуры. Так, если осуществить синтез воды при 20оС даже на 15% практически невозможно (на это потребовалось бы 54 миллиарда лет), то при 500оС для этого необходимо всего 50 минут, а при 700оС реакция происходит мгновенно. – число десятков градусов изменения температуры.
– число десятков градусов изменения температуры.
 (1.20)
(1.20) выражает так называемый стерический фактор, который также может существенно влиять на скорость реакции. Его смысл в том, что, кроме обладания энергией активации, для осуществления реакции необходимо, чтобы молекулы при столкновении были определённым образом (благоприятно) ориентированны друг относительно друга в пространстве. Это можно проиллюстрировать на примере реакции
выражает так называемый стерический фактор, который также может существенно влиять на скорость реакции. Его смысл в том, что, кроме обладания энергией активации, для осуществления реакции необходимо, чтобы молекулы при столкновении были определённым образом (благоприятно) ориентированны друг относительно друга в пространстве. Это можно проиллюстрировать на примере реакции

 часто обозначают как А и называют предэкспоненциальным множителем, тогда уравнение (1.20) записывается:
часто обозначают как А и называют предэкспоненциальным множителем, тогда уравнение (1.20) записывается: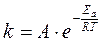 (1.21)
(1.21) (1.22)
(1.22) , то получим прямую, отсекающую на оси ординат отрезок, равный lgA (откуда можно определить А) и имеющую наклон, равный
, то получим прямую, отсекающую на оси ординат отрезок, равный lgA (откуда можно определить А) и имеющую наклон, равный 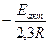 (откуда можно определить Ea) (рис. 12):
(откуда можно определить Ea) (рис. 12):
 .
.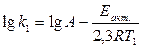 (1.23)
(1.23) (1.24)
(1.24)