 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Інтегрування деяких ірраціональних функцій ⇐ ПредыдущаяСтр 5 из 5
Розглянемо деяки типи інтегралів, що містять ірраціональні функції. Для знаходження інтеграла від ірраціональної функції слід застосувати підстановку, яка перетворює цю функцію до раціональної форми, інтеграл від якої може бути знайдений. Інтеграл вигляду За допомогою підстановки
Тоді Приклад.
Якщо до складу ірраціональної функції входить коріння різних степенів, то у якості нової змінної треба узяти корінь степені, рівної найменшому загальному кратному степенів коріннів, що входять у вираз. Проілюструємо це на прикладі. Приклад.
Інтеграли вигляду Існує декілька способів інтегрування такого роду функцій. Залежно від вигляду виразу, що стоїть під знаком радикала, переважно застосовувати той або інший спосіб. Як відомо, квадратний тричлен шляхом виділення повного квадрата може бути приведений до вигляду:
Таким чином, інтеграл наводиться до одного з трьох типів: 1) 2) 3) Можливі три способи інтегрування таких функцій. 1). Тригонометрична підстановка Інтеграл вигляду Приклад.
Інтеграл вигляду Приклад:
Інтеграл вигляду Приклад.
2. Підстановки Ейлера 1. Якщо а > 0, то інтеграл вигляду 2. Якщо а < 0 і с > 0, то інтеграл вигляду 3. Якщо а < 0, а підкорінний вираз розкладається на дійсні множники a (x – x1)(x – x2), те інтеграл вигляду Відзначимо, що підстановки Ейлера незручні для практичного використання, оскільки навіть при нескладних підінтегральних функціях наводять до вельми громіздких обчислень. 3. Метод невизначених коефіцієнтів. Розглянемо інтеграли наступних трьох типів:
де P(x) – многочлен, n – натуральне число. Причому інтеграли II і III типів можуть бути легко приведені до вигляду інтеграла I типа. Інтеграли типа I можна обчислювати, користуючись формулою
де Q(x) - деякий многочлен, степінь якого нижча за степінь многочлена P(x), а (l - деяка постійна величина. Для знаходження невизначених коефіцієнтів многочлена Q(x), степінь якого нижча за степінь многочлена P(x), диференціюємо обоє частини даного виразу, потім умножають на Даний метод вигідно застосовувати, якщо степінь многочлена Р(х) більше одиниці. Інакше можна успішно використовувати методи інтегрування раціональних дробів, які розглянуті вище, оскільки лінійна функція є похідною підкорінного виразу. Приклад.
Диференціюємо цей вираз, потім помножимо на
=
Прирівняємо коефіцієнти при однакових степенях х
Таким чином,
= Приклад.
Приклад.
Отже
Поиск по сайту: |
,де n- натуральне число.
функція раціоналізується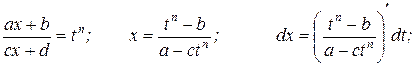
=
=
.
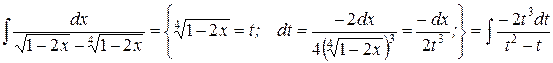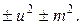
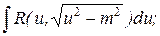
підстановкою 
або 
зводиться до інтеграла від раціональної функції відносно sin t або cos t.
підстановкою 
або 
зводиться до інтеграла від раціональної функції відносно sin t і cos t.
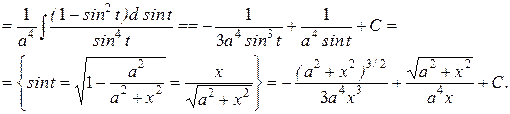
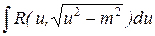підстановкою 
або 
зводиться до інтеграла від раціональної функції відносно sin t або cos t.
раціоналізується підстановкою 
.
.
.
,
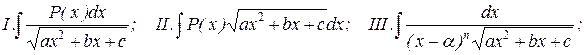
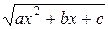і, порівнюючи коефіцієнти при однакових степенях х, визначають λ і коефіцієнти многочлена Q(x).
.
= 
=
.
=
, 
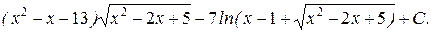
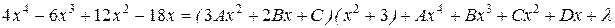
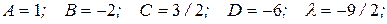
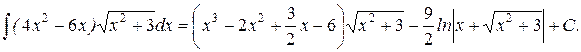
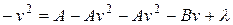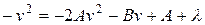. Звідки
.
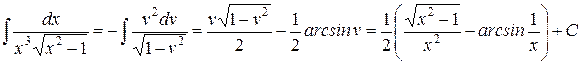