 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Через координаты сомножителей. Матрица Грама
Пусть в евклидовом n-мерном пространстве
где Выразим скалярное произведение
где обозначено
где матрица
Определение 3.4.Матрица (3.6) порядка Замечание 3.3. Матрица Грама может быть построена, вообще говоря, для любой произвольной системы векторов
Сформулируем простейшие свойства матрицы Грама. Теорема 3.3. Матрица Грама является симметрической ( □ Справедливость утверждения вытекает из аксиомы Теорема 3.4 (критерий Грама линейной зависимости системы векторов). Система векторов □ Необходимость. Пусть система векторов
Умножая последовательно последнее равенство скалярно на векторы
Определителем этой системы является определитель
то определитель Достаточность доказывается, проводя рассуждения в обратном порядке. ■ Теорема 3.5 (изменение матрицы Грама при переходе к другому базису). Пусть в евклидовом пространстве
Связь между матрицами Грама
где Доказательство теоремы построено на использовании равенства (3.5) и формул преобразования координат при переходе от базиса к базису. Пример 3.1. В линейном пространстве
Записать матрицы Грама Решение.Составим матрицы Грама
этих матриц. Имеем
В результате получим матрицы
Нетрудно убедиться в справедливости равенства (3.8), которое в нашем случае имеет вид
Поиск по сайту: |
 задан некоторый базис
задан некоторый базис  . Разложим векторы
. Разложим векторы 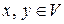 по базису
по базису 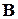 :
:
 координатные вектор-столбцы векторов
координатные вектор-столбцы векторов 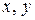 в базисе
в базисе 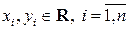 ).
).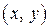 векторов
векторов 

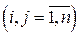 . Последнее равенство можно переписать в матричной форме
. Последнее равенство можно переписать в матричной форме , (3.5)
, (3.5) (3.6)
(3.6) называется матрицей Грама системы векторов
называется матрицей Грама системы векторов  базиса
базиса  евклидова пространства. В этом случае мы получаем матрицу
евклидова пространства. В этом случае мы получаем матрицу 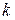 -го порядка:
-го порядка: (3.7)
(3.7) ).
).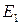 евклидова пространства:
евклидова пространства: 
 матрицы Грама
матрицы Грама  этой системы равен нулю.
этой системы равен нулю.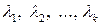 , среди которых существует по крайней мере одно ненулевое такие, что
, среди которых существует по крайней мере одно ненулевое такие, что .
. , получим однородную систему, состоящую из
, получим однородную систему, состоящую из 
 .
. . Так как эта система имеет ненулевое решение
. Так как эта система имеет ненулевое решение ,
, ,
, 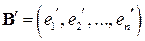 .
. и
и 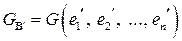 для этих базисов описывается равенством
для этих базисов описывается равенством , (3.8)
, (3.8)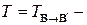 матрица перехода от базиса
матрица перехода от базиса  к базису
к базису  .
. со скалярным произведением
со скалярным произведением 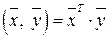 заданы базисы
заданы базисы  и
и  :
: .
. и
и  для базисов
для базисов 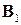 и
и  , проверить выполнимость равенства (3.8).
, проверить выполнимость равенства (3.8).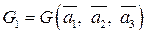 и
и  для базисов
для базисов  ,
,  (
( 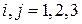 )
)
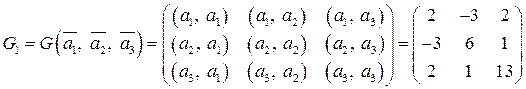 ,
, .
. , где
, где ,
, 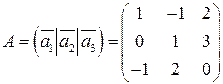 ,
, .
.