 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Примеры евклидовых пространствСтр 1 из 5Следующая ⇒
Евклидовы пространства Понятие евклидова линейного пространства. Примеры евклидовых пространств Пусть задано линейное пространство. Возникает вопрос: можно ли измерять расстояние между элементами (векторами) этого пространства, находить углы между векторами и длины (модули) этих векторов. Ответы на этот вопрос дает понятие евклидова линейного пространства. Определение 3.1.Если в линейном пространстве
то это пространство называется евклидовым пространством. Число Аксиома Поскольку евклидово пространство является линейным, то на него переносятся все понятия, определенные для линейного пространства. В частности, можно ввести понятие базиса и размерности евклидова пространства. Сформулируем простейшие следствия из аксиом евклидова пространства: 1) 2) 3) Теорема 3.1. В евклидовом пространстве
□ Отбрасывая тривиальный случай, когда один из векторов
Преобразовав скалярное произведение согласно аксиомам, получим
Левую часть полученного неравенства можно рассматривать как квадратный трехчлен относительно
откуда и следует неравенство (3.1). ■ В данном пункте приведены примеры наиболее часто встречающихся евклидовых пространств. Заметим, что в одном и том же линейном пространстве скалярное произведение можно ввести различными способами. Рассмотрим различные способы задания скалярного произведения в двух линейных пространствах Рассмотрим линейное пространство Первый способ (задание скалярного произведения стандартным образом):
Покажем, что при таком задании скалярного произведения в
Второй способ (задание скалярного произведения в виде симметрической билинейной формы):
где Замечание 3.1.Доказательство того факта, что скалярное произведение, заданное в виде симметрической билинейной формы, удовлетворяет всем аксиомам евклидова пространства, можно посмотреть в п. 6.7. Замечание 3.2.Так Рассмотрим линейное пространство
Первый способ задания скалярного произведения:
Второй способ задания скалярного произведения:
где Можно показать, что в каждом случае выполняются все аксиомы евклидова пространства.
Поиск по сайту: |
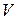 любым двум элементам
любым двум элементам 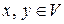 можно поставить в соответствие действительное число
можно поставить в соответствие действительное число  , называемое скалярным произведением векторов
, называемое скалярным произведением векторов 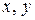 и удовлетворяющее аксиомам:
и удовлетворяющее аксиомам:
 ,
,
 ,
, 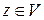 ,
,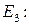
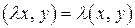 ,
,  ,
,
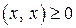 , причем
, причем 
 ,
, называется скалярным квадратом вектора
называется скалярным квадратом вектора 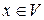 .
.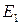 определяет симметричность скалярного произведения, аксиомы
определяет симметричность скалярного произведения, аксиомы  – аддитивность и однородность по первому множителю,
– аддитивность и однородность по первому множителю,  неотрицательность скалярного квадрата.
неотрицательность скалярного квадрата. ,
,  ,
,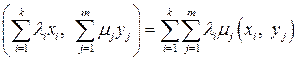
 ,
, .
. для любых двух векторов
для любых двух векторов 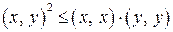 . (3.1)
. (3.1) . Рассмотрим при произвольном числе
. Рассмотрим при произвольном числе  и найдем его скалярный квадрат
и найдем его скалярный квадрат .
. .
. ), принимающий неотрицательные значения при каждом
), принимающий неотрицательные значения при каждом  ,
, и
и 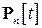 .
. . Скалярное произведение в нем можно задать двумя способами.
. Скалярное произведение в нем можно задать двумя способами.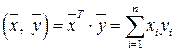 .
.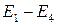 евклидова пространства. Действительно, при всех
евклидова пространства. Действительно, при всех  ,
,  ,
, ,
, ,
, , причем
, причем 
 .
.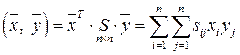 ,
,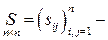 симметрическая (
симметрическая ( 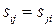 ,
, 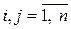 ) положительно определенная матрица
) положительно определенная матрица  -го порядка.
-го порядка. и
и 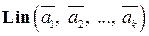 являются подпространствами евклидова пространства
являются подпространствами евклидова пространства 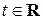 степеней, не превосходящих натуральное число
степеней, не превосходящих натуральное число 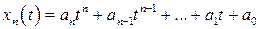 ,
,  .
. .
.
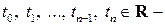 попарно различные действительные числа.
попарно различные действительные числа.