 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задания для самостоятельной работы. № 4. Осуществить циклический сдвиг компонент заданного вектора A(N) влево на одну
Составьте блок-схемы для решения следующих задач. № 1. Вычислить сумму квадратов всех элементов заданного массива X(N), за исключением элементов, кратных пяти. № 2. В заданном массиве A(N) поменять местами наибольший и наименьший элементы. № 3. В заданном массиве A(N) определить количество элементов, которые меньше заданного значения. № 4. Осуществить циклический сдвиг компонент заданного вектора A(N) влево на одну позицию, то есть получить вектор А = (a2 , a3, ..., aN, a1 ). № 5. Дан массив A(N). Получить массив B(N), i-й элемент которого равен среднему арифметическому первых i элементов массива А: bi = (a1 + a2 + ... + ai)/i. № 6. В заданном массиве A(N), все элементы которого попарно различны, найти: а) наибольший элемент из отрицательных; б) наименьший элемент из положительных; в) второй по величине элемент. № 7. Образовать массив B, состоящий из положительных элементов заданного массива A(N), больших пяти. Вывести на печать образованный массив и число его элементов. № 8. Дана матрица A(3, N), элементы которой положительны. Определить, какие из троек a1i , a2i, a3i (i = 1, ..., N) могут служить сторонами треугольника. Вывести массив b1 , ..., bN , состоящий из нулей и единиц. Если тройка a1i, a2i , a3i может служить сторонами треугольника, то bi = 1, если нет, то № 9. Дана матрица A(N,M). Вычислить вектор X(M), где значение Xj равно сумме положительных элементов j-го столбца матрицы A. № 10. Дана матрица A(N,M). Получить вектор X(M), равный P-й строке матрицы, и вектор Y(N), равный Q-му столбцу матрицы. № 11. Дана матрица A(N,M). Поменять местами её наибольший и наименьший элементы. № 12. В заданной матрице A(N, M) поменять местами столбцы с номерами P и Q. № 13. По трём заданным матрицам А(N,N), В(N,N) и С(N,N) построить матрицу Х того же размера, каждый элемент которой вычисляется по формуле № 14. Дана матрица A(N,M). Определить: а) число ненулевых элементов в каждой строке матрицы; б) общее число ненулевых элементов в матрице; в) отношение числа ненулевых элементов в каждой строке матрицы к общему числу ненулевых элементов в матрице.
Алгоритмы оптимизации на сетях и графах Основные понятия: · граф; · остовное дерево графа; · алгоритмы Прима и Краскала; · алгоритм Дейкстры; · сеть; · поток; · задача Форда-Фалкерсона о потоках в сетях. Теоретический материал Алгоритм вычисления остовного дерева наименьшего веса
Определение 1.Граф – это непустое множество точек (вершин), связанных между собой определенными отношениями. Определение 2.Остовное дерево графа – это подграф данного графа, содержащий все его вершины. Для вычисления остовного дерева наименьшего веса применяются два алгоритма: алгоритм Прима и алгоритм Краскала. Алгоритм Прима состоит в удалении длиннейших ребер и проверке связности графа после каждого удаления. Алгоритм Краскаласостоит в выборе кратчайшего ребра и присоединении к нему кратчайшего из связанных с ним ребер; после каждого присоединения выполняется проверка отсутствия циклов.
Пример 4.1. Построить остовное дерево наименьшего веса для следующих графов. а) Решение Воспользуемся алгоритмом Краскала.
2. Присоединяем к нему ребро DE, тогда возможность выбора ребра CЕ в дальнейшем отпадает, т.к. получится цикл. 3. Присоединяем ребро FC к ребру CD. Циклов нет. 4. Присоединяем AF к FC. Циклов нет. 5. Присоединяем АВ к AF. Циклов нет. В результате получили остовное дерево, вес которого равен сумме весов ребер: 1+3+3+1+2=10.
Решение Применим алгоритм Прима. 1.Удалим петлю ЕЕ. 2.Удаляем длиннейшее ребро АС, при этом граф остается связным. 3.Удаляем ребро АЕ длины 4. Граф связный. 4.Удаляем ребро АD длины 3. Граф связный. 5.Удаляем ребро СЕ. Получаем искомое остовное дерево. Вес полученного дерева равен 1+1+2+2=6. Алгоритм Дейкстры для решения задачи о кратчайших путях
Задача о кратчайшем пути. Имеется N городов, соединенных дорогами. Необходимо найти кратчайшие пути из одного города ко всем остальным. Для решения задачи необходимо построить матрицу графа. Затем, используя вспомогательные таблицы, найти кратчайшие пути от заданной вершины к остальным в соответствии с алгоритмом Дейкстры. Работу алгоритма рассмотрим на примере. Пример 4.2. Найти кратчайшее расстояние от вершины 1 до всех остальных и восстановить путь от 1 до 7.
Составим матрицу данного графа.
Так как требуется найти кратчайшее расстояние от вершины 1 до всех остальных, то будем рассматривать первую строку составленной матрицы. Шаг 1. Составим вспомогательную таблицу. В этой таблице в строчке а будем отмечать рассмотренные вершины; в строке b – длины путей; в строке с – номер вершины, через которую проходит кратчайший путь.
Шаг 2. Из всех длин путей от вершины 1 до других вершин выбираем вершину 3, т.к. длина пути 1-3 наименьшая и равна 12. Из первой вершины попасть в четвертую можно через третью, поэтому длина пути 1-4 станет равной сумме длин путей 1-3 и 3-4, то есть 12+18=30 (30 < ∞). В строку b записываем длину пути от 1 до 4 равную 30. Ни к какой другой вершине графа попасть через вершину 3 на данном шаге не удается. Таблица примет вид
Шаг 3. Отмечаем вершину 2.
Пути к 5 и 8 вершинам найдены сложением путей 1-2 и 2-5, 1-2 и 2-8 соответственно. Шаг 4. Минимальный путь из неотмеченных вершин – 30 – лежит через 4 вершину, поэтому отмечаем вершину 4.
Шаг 5. Отмечаем вершину 5.
Шаг 6. Отмечаем вершину 6.
Все возможные пути через вершину 6 оказываются длиннее, чем уже определенные, поэтому пути остаются без изменения. Шаг 7. Проверим пути через вершину 8.
Видим, что проверка длин путей от 1 к остальным через 8 вершину не дает более коротких путей. Восстановим путь от 1 до 7 вершины. Проведем восстановление в обратном порядке: в вершину 7 можно попасть, пройдя через вершину 5, а в вершину 5 – через вершину 2; вершины 1 и 2 связаны напрямую. Таким образом, получаем путь 1→2→5→7, длина которого равна 59. Потоки в сетях.
Поиск по сайту: |
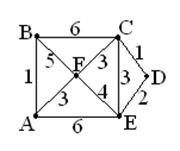
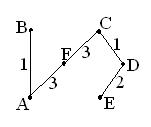 1. Выбираем ребро CD.
1. Выбираем ребро CD. б)
б) 
 Решение
Решение