 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Теоретический материал. Формула Хартли для определения количества информации:
Формула Хартли для определения количества информации:
Формула Шеннона для определения количества информации:
Множество символов, используемых при записи текста, называется алфавитом. Полное количество символов в алфавите называется мощностью алфавита. Количество информации, которую несет каждый символ, вычисляется по формуле
Количественная зависимость между вероятностью события и количеством информации в сообщении о нем выражается формулой
Пример 1.1. Чему равно количество информации, если получено сообщение о выходе из строя одного из 8 станков в цехе.
Решение Так как выход из строя любого станка есть событие равновероятное, то Ответ: 3.
Пример 1.2. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем шаре. Решение Так как выпадение любого шара есть событие равновероятное, то N = 32. Тогда количество информации об одном номере равно I = log232 = 5 (бит). Ответ: 5. Пример 1.3. Алфавит состоит из букв a, b, c, d. Вероятности появления равны соответственно 0,25; 0,25; 0,34; 0,16. Определить количество информации, приходящейся на символ сообщения, составленного из букв этого алфавита. Решение Количество информации на один символ есть энтропия (мера неопределённости) данного алфавита. Так как символы не равновероятны, то количество информации найдем с помощью формулы Шеннона: I = – (2·0,25·log20,25 + 0,34·log20,34 + 0,16·log20,16) = 1,95 (бит). Ответ: 1,95. Пример 1.4. Книга, набранная на компьютере, содержит 150 страниц, на каждой странице 40 строк, в каждой строке 60 символов. Каков объем информации в книге? Решение Мощность компьютерного алфавита равна 256 символов, тогда количество информации, которую несет один символ I = log2256 = 8 (бит) = 1 (байт). Объем строки равен 60 байт, объем страницы равен 40 · 60 = 2400 (байт). Объем всей книги равен 2400 · 150 = 360 000 байт = 351,5625 Кбайт = 0,34 Мбайт. Ответ: 0,34 Мбайт.
Графическая информация Определение 1. Разрешающая способность экрана – размер сетки растра, задаваемого в виде произведения М х N, где М – число точек по горизонтали, N – число точек по вертикали (число строк). Число цветов, воспроизводимых на экране дисплея (К), и число бит, отводимых в видеопамяти под каждый пиксель (N), связаны формулой К = 2N. Пример 1.5.Сколько бит видеопамяти занимает информация об одном пикселе на черно-белом экране (без полутонов)? Решение Для черно-белого изображения без полутонов К = 2. Следовательно, 2N = 2. Отсюда N = 1 бит на пиксель. Ответ: 1 бит.
Величину N называют битовой глубиной. Пример 1.6.На экране с разрешающей способностью 640 × 200 высвечиваются только двухцветные изображения. Какой минимальный объем видеопамяти необходим для хранения изображения? Решение Так как битовая глубина двухцветного изображения равна 1, а видеопамять как минимум должна вмещать одну страницу изображения, то объем видеопамяти равен Q = 640 ∙ 200 ∙ 1 = 128000 бит = 16000 байт. Ответ: 16000 байт.
Звуковая информация Определение 2. Частота дискретизации – это количество измерений входного сигнала за 1 секунду. Частота измеряется в герцах (Гц). Одно измерение за одну секунду соответствует частоте 1 Гц. 1000 измерений за 1 секунду – 1 килогерц (кГц). Характерные частоты дискретизации аудиоадаптеров: 11 кГц, 22 кГц, 44,1 кГц и др. Определение 3. Разрядность регистра – число бит в регистре аудиоадаптера. Формула для расчета размера (в байтах) цифрового аудиофайла при монофоническом звучании: (частота дискретизации, Гц) ∙ (время записи, сек) ∙ (разрешение, бит)/8. Пример 1.7. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен. Решение Размер файла вычисляется по формуле Q = 22050 ∙ 10 ∙ 8 / 8 = 220500 байт. Ответ: 220500 байт. Оптимальное кодирование
Одно и то же событие можно закодировать разными способами. Оптимальным будет считаться такой код, при котором на передачу сообщения затрачивается минимальное время. Если на передачу каждого элементарного символа тратится одно и то же время, то оптимальным будет такой код, который имеет минимально возможную длину. Возникает вопрос: возможно ли составить код, в котором на одну букву будет в среднем приходиться меньше элементарных символов? Такие коды существуют. Это коды Шеннона-Фано и Хаффмана. Принцип построения оптимальных кодов: 1) каждый элементарный символ должен переносить максимальное количество информации, для этого необходимо, чтобы элементарные символы 2) необходимо буквам первичного алфавита, имеющим большую вероятность, присваивать более короткие кодовые слова вторичного алфавита. Пример 1.8. Пусть имеется случайная величина Х(х1,…,х8), имеющая 8 состояний с распределением вероятностей Р( Решение Длина равномерного кода k для алфавита из m символов k = log2m. Для кодирования алфавита из 8 букв без учета вероятности равномерным двоичным кодом нам понадобится k = log28 = 3 (символа). Тогда получаем коды:
Чтобы определить, насколько возможно сокращение длины кода, необходимо вычислить избыточность
Таким образом, возможно сокращение длины минимального кода на 8,4 %. Пример 1.9. Закодировать кодами Шеннона-Фано и Хаффмана алфавит, состоящий из пяти букв а1, а2, а3, а4, а5 вероятности появления которых соответственно равны 0,4; 0,3; 0,15; 0,1; 0,05. Решение
Определим, какова средняя длина полученного кода. Для этого подсчитаем среднее число символов, приходящихся на букву:
Энтропия данной системы равна:
Таким образом, средняя длина получилась достаточно близкой к предельному значению. Длина кода при равномерном кодировании k = 3 бита. Код Шеннона-Фано по сравнению с равномерным кодированием позволил сократить среднюю длину кодовых комбинаций для данного примера на 31,6 % (L = 1 – 2,05/3 = 0,316). При составлении кода Хаффмана строится следующая схема:

а1– 0; а2 – 11; а3 – 101; а4 – 1001; а5 – 1000. Средняя длина кода
Метод сжатия данных Лемпела-Зива
Системы кодирования по методу Лемпела-Зива используют технологию кодирования с применением адаптивного словаря. Здесь под термином «словарь» понимается набор блоков, из которых создается сжатое сообщение. Процесс сжатия начинается с переписывания начальной части сообщения, однако в определенный момент осуществляется переход к представлению будущих сегментов с помощью триплетов, каждый из которых будет состоять из двух целых чисел и следующего за ними одного символа текста. Каждый триплет описывает способ построения следующей части сообщения. Пример 1.10. Разархивировать сообщение, сжатое методом Лемпела-Зива: 0100101(4,3,0)(8,7,1). Решение Строка 0100101 является уже распакованной частью сообщения. Далее необходимо расширить строку, присоединив к ней ту часть, которая в ней уже встречается. Первый номер в триплете указывает, сколько символов необходимо отсчитать в обратном направлении в строке, чтобы найти первый символ добавляемого сегмента. В данном случае необходимо отсчитать в обратном направлении 4 символа, и мы попадем на четвертый слева символ – 0 – уже распакованной части строки. Второе число в триплете задает количество последовательных символов справа от начального, которые составляют добавляемый сегмент. В нашем случае это число 3, а это означает, что добавляемый сегмент – 010. Добавляем его в конец строки и получаем новое значение распакованной части сообщения: 0100101010. Последний элемент триплета – 0 – должен быть помещен в конец строки. В результате получаем: 01001010100. Рассуждая аналогично, раскрываем второй триплет. В итоге получим результат: 0100101/0100/01010101. Проверим по количеству цифр: всего получили код из 19 цифр, из триплетов имеем 7+3+1+7+1=19.
Пример 1.11. Сжать сообщение методом Лемпела-Зива: 11011101110111100011. Решение 1101/110/11101/11100/011 (4,2,0) (4,4,1) (5,4,0) (7,2,1)
Ответ: 1101(4,2,0)(4,4,1)(5,4,0)(7,2,1).
Коды с исправлением ошибок Определение 4.Дистанция Хемминга – количество битов, отличающихся в кодовых комбинациях. Пример 1.12. Дан код
Получена битовая комбинация 010100 с ошибкой. Расшифруйте сообщение, исправив ошибку. Решение Для исправления ошибки необходимо вычислить дистанцию Хемминга между битовыми комбинациями символов алфавита и полученной битовой комбинацией.
Поступивший код соответствует букве D, т.к. её битовая комбинация в наибольшей степени соответствует полученной.
Поиск по сайту: |
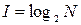 .
. .
. .
. ,
,  ,
,  ,
,  , где I – энтропия оптимального значения, k–длина равномерного кода.
, где I – энтропия оптимального значения, k–длина равномерного кода. .
. .
. (бит).
(бит). (бит).
(бит).