 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЭЛЕКТРОПРИВОДА ПРИ ПРОИЗВОЛЬНОЙ ЗАВИСИМОСТИ ДИНАМИЧЕСКОГО МОМЕНТА ОТ СКОРОСТИ ⇐ ПредыдущаяСтр 5 из 5
В общем случае динамический момент, определяемый моментами двигателя и исполнительного органа, зависит от скорости, положения исполнительного органа и времени, в том числе и произвольным образом. Рассмотрим неустановившееся движение, когда аналитическая зависимость динамического момента от скорости отсутствует. Нахождение искомых зависимостей M(t), w(t) и j(t) связано с решением (интегрированием) основного уравнения движения (1.11) при заданных законах изменения моментов двигателя и нагрузки. Если эти законы выражаются аналитически, то основные проблемы имеют математический, характер и связаны с интегрированием уравнения (1.11). Когда законы изменения моментов не заданы аналитически или точное решение (1.11) невозможно, используются приближенные способы интегрирования уравнения движения: численные и графоаналитические. Рассмотрим применение этих методов при произвольной зависимости моментов, только от скорости движения.
Численные методы интегрирования дифференциальных уравнений широко используются в вычислительной математике и известны под названием методов Эйлера, Рунге ‑ Кутта и др. Рассмотрим применение наиболее простого из них — метода Эйлера на примере получения зависимости w(t) при пуске АД с вентилятором, механические характеристики приведены на рис. 1.13, а. Метод Эйлера предусматривает замену дифференциалов переменных в (1.11) их приращениями, в результате чего это уравнение может быть записано в виде
Для пользования этим уравнением ось скорости разбивается на ряд интервалов До,, на которых моменты АД и нагрузки (вентилятора) принимаются постоянными. Далее для удобства вычислений составляется табл. 1.1. Таблица 1.1
Порядок расчета зависимости w(t) состоит в следующем. Для каждого i-го интервала скорости При необходимости построение зависимости j(t) уравнение Достоинство рассмотренного численного метода состоит в его простоте и наглядности, а точность его определяется интервалами Графические и графоаналитические методы, среди которых наибольшее распространение получили метод площадей и метод пропорций, также предназначены для приближенного интегрирования уравнения движения для получения зависимостей M(t), w(t) и (р(0. Рассмотрим сущность метода пропорций на том же примере пуска АД вентилятора. В основе этого метода также лежит представление переменных в (1.11) в виде приращений
Построение осуществляется следующим образом (рис. 1 14). В левом квадранте строим характеристики М(w), Мс(w) и графически находим зависимость динамического момента от скорости Мдин(w).
Далее ось скорости разбиваем на ряд интервалов, на. каждом из которых динамический момент принимается постоянным. Затем полученные на каждом интервале значения Мдин в определенном масштабе тм откладываем по оси ординат, получаем отрезки OM1, OM2 и т. д. На оси абсцисс в масштабе т, откладываем пропорциональный моменту инерции J отрезок ON и точку N соединяем с точками Действительно, Аналогичным построением для остальных участков разбиения оси скорости может быть получена искомая кривая w(t), показанная в первом квадранте рис. 1.14. Отметим одно обстоятельство, которое должно учитываться при использовании этого метода. В соответствии с (1.43) масштабы тм , тJ ,тw и mt; должны быть связаны между собой соотношением
Поэтому независимо от остальных могут быть выбраны только масштабы трех величин, а масштаб четвертой должен быть определен из пропорции (1.44).
Поиск по сайту: |

 (1.42)
(1.42)







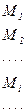



 по характеристикам рис. 1.13, а определяют средние на этом интервале моменты двигателя Mi (столбец 3) и нагрузки МCi (столбец 4). Далее по (1.42) рассчитывают
по характеристикам рис. 1.13, а определяют средние на этом интервале моменты двигателя Mi (столбец 3) и нагрузки МCi (столбец 4). Далее по (1.42) рассчитывают 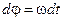 также записывается в приращениях
также записывается в приращениях  , и по данным столбцов 2 и 5 может быть получена и эта зависимость.
, и по данным столбцов 2 и 5 может быть получена и эта зависимость. разбиения оси скорости.
разбиения оси скорости. (1.43)
(1.43)
 и т. д. Далее из начала координат проводим прямую ОА1, параллельную NM1, до пересечения с горизонтальной линией, соответствующей верхней границе первого интервала скорости. Этот отрезок ОА1 представляет собой график скорости w(t) на первом интервале движения.
и т. д. Далее из начала координат проводим прямую ОА1, параллельную NM1, до пересечения с горизонтальной линией, соответствующей верхней границе первого интервала скорости. Этот отрезок ОА1 представляет собой график скорости w(t) на первом интервале движения. , но
, но  ~
~ 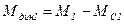 ; ON~J;
; ON~J;  ~
~ 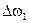 , следовательно, в соответствии с (1.43)
, следовательно, в соответствии с (1.43)  ~
~  .
. (1.44)
(1.44)