 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЭЛЕКТРОПРИВОДА ПРИ ПОСТОЯННОМ ДИНАМИЧЕСКОМ МОМЕНТЕ
Неустановившееся механическое движение электропривода возникает во всех случаях, когда момент двигателя отличается от момента нагрузки, т. е. когда Рассмотрение неустановившегося движения электропривода имеет своей основной целью получение зависимостей изменения во времени выходных механических координат электропривода ‑ момента M(t), скорости w(t) и положения вала двигателя j(t). Кроме того, часто требуется определить время неустановившегося движения (переходного процесса) электропривода. Отметим, что законы изменения моментов двигателя и нагрузки должны быть предварительно заданы. Рассмотрим неустановившееся движение одномассовой системы, показанной на рис. 1.1, б, при неизменном и отличном от нуля динамическом моменте. Такое движение возникает в том случае, когда механические характеристики двигателя и исполнительного органа параллельны, например вертикальны, как это показано на рис. 1.8, а. Искомые зависимости изменения координат электропривода во времени получаются путем решения (интегрирования) основного уравнения движения (1.11). В рассматриваемом случае оно относится к классу дифференциальных уравнений с разделяющимися переменными
откуда при учете М—Mс = const находим
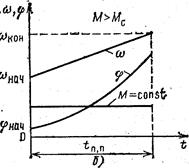
Рис. 1.8. Переходные процессы при постоянных моментах двигателя и исполнительного органа: а—механические характеристики двигателя а исполнительного органа; б— графики переходного процесса
Постоянная интегрирования С1 определяется из начальных условий: при t=0 w = wнач, откуда С1 = wнач. Окончательно получаем
Из (1.25) следует, что при МДИН=М–Мс=const скорость есть линейная функция времени. Она увеличивается при М–Мс>0 и уменьшается при М—Мс<0. На рис. 1.8, б показан процесс изменения скорости w(t) при М—Мс>0. Там же показан график момента двигателя M(t), представляющий собой в данном случае горизонтальную линию М=const. Выражение (1.25) позволяет определить время переходного процесса tп.п, т. е. время изменения скорости от начального wнач до некоторого конечного wкон значения. Полагая в (1.25) w =wкон и t=tп.п, находим
График изменения угла поворота вала двигателя во времени j(t) находится путем интегрирования (1.25) с учетом равенств w=dj /dt и dj=wdt
или
При t=0 j=jнач, откуда С2=jнач. Окончательно для изменения угла поворота j(t) получаем
Из (1.27) видно, что зависимость j(t) имеет параболический характер; она также приведена на рис. 1.8, б. Несмотря на кажущуюся идеализированность рассмотренного случая, полученные аналитические соотношения часто используют при выполнении различных приближенных расчетов в электроприводе при рассмотрении его неустановившегося движения. Один из таких расчетов иллюстрирует пример 1.2. Пример 1.2. Требуется ориентировочно оценить время разбега вхолостую (Мс=0) АД, имеющего характеристику, показанную на рис. 1.9, и следующие технические данные: скорость идеального холостого хода w0=314 рад/с; пусковой момент Мп=80 Н×м; максимальный (критический) момент Мк=120 Н×м; момент инерции ротора J=0,2 кг×м2.
Рис. 1.9. К расчету ориентировочного времени пуска асинхронного двигателя
Точное определение времени разбега АД с показанной нелинейной характеристикой связано с определенными трудностями. Если же ограничиться лишь оценкой этого времени, то задача упрощается и решается следующим образом. Реальная характеристика двигателя j(М) заменяется прямоугольной, как это показано на рис. 1.9 штриховой линией. Средний момент Мср, определяемый обычно как полусумма пускового Mп и критического Мк моментов, т. е. Мср = (Mп + Мк)/2, принимается за время разбега двигателя неизменным. Тогда справедливы все выводы этого параграфа и время разбега tразб= tп.п определится по (1.26) tразб= tп.п = J×(wо - 0)/(Мср - 0) = 0,2×314/100 = 0,63 с. Аналогичные расчеты могут быть выполнены для нелинейных механических характеристик и других видов переходных режимов: торможения, реверса, переходе с характеристики на характеристику.
1.6. НЕУСТАНОВИВШЕЕСЯ ДВИЖЕНИЕ ЭЛЕКТРОПРИВОДА ПРИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ МОМЕНТОВ ДВИГАТЕЛЯ И ИСПОЛНИТЕЛЬНОГО ОРГАНА ОТ СКОРОСТИ Рассматриваемый вид движения является весьма распространенным. Он, в частности, характерен для переходных процессов в электроприводе с двигателем постоянного тока независимого возбуждения и частично для асинхронного электропривода. Получение общих аналитических выражений для изменения скорости и момента двигателя во времени проведем с помощью рис. 1.10, где представлены линейные .механические характеристики двигателя Д и исполнительного органа ИО. Аналитически эти характеристики могут быть соответственно представлены как
где Мк.з и Мс0 — моменты двигателя и исполнительного органа при w=0.
Рис. 1.10. Линейные механические характеристики двигателя и их исполнительного органа
Выражая в (1.11)
Поделив уравнение (1.29) почленно на
где Решение (1.30) будем искать как сумму общего решения линейного однородного уравнения (свободной составляющей движения)
и частного решения неоднородного уравнения (1.30) (принужденной составляющей движения), т. е. в виде
Свободную составляющую движения в соответствии с уравнением (1.31) найдем в виде
Из (1.33) находим корень характеристического уравнения
Принужденная составляющая движения может быть получена, если в (1.30) положить
С учетом (1.34) и (1.35) представим решение (1.30) в виде
Константу А находим по начальным условиям переходного процесса: при Окончательно для скорости получаем
Так как скорость и момент двигателя связаны линейной зависимостью [первое уравнение (1.28)], закон изменения момента в функции времени имеет вид, аналогичный (1.37),
Для нахождения зависимости угла поворота вала двигателя от скорости необходимо проинтегрировать дифференциальное уравнение
Полученные выражения (1.37) ‑ (1.39) могут использоваться для анализа переходных процессов различного вида ‑ пуска, реверса, торможения и т. д. Для пользования ими в каждом конкретном случае должна быть определена электромеханическая постоянная времени Тм, а также начальные и конечные значения координат
Выражения (1.37) и (1.38) позволяют определить время
Электромеханическая постоянная времени
Из полученного соотношения видно, что электромеханическая постоянная времени
Если провести касательную к экспонентам w(t) или M(t) в точке t=0, то отрезок, отсекаемый касательной на уровне установившегося значения wуст или Mуст, равен в масштабе времени постоянной времени Ти, как показано на рис. 1.12. Электромеханическая постоянная времени Полученные выражения (1.37)—(1.39) справедливы для непрерывных линейных механических характеристик двигателя и исполнительного органа. Если же одна из них имеет разрыв, как, например, характеристика момента трения, то переходный процесс рассчитывается по участкам, при этом конечные значения координат на предыдущем участке равны начальным значениям на следующем участке. Пример 1.3. Построить зависимости w(t) и M(t) при пуске двигателя, имеющего линейную механическую характеристику w(M), при следующих исходных данных скорость идеального холостого хода двигателя w0=157 рад/с, момент короткого замыкания 1. Вначале определим электромеханическую постоянную
2 Найдем начальные и конечные значения переменных: 3 Выражения для скорости и момента в соответствии с (1.37) и (1.38) принимают вид
В соответствии с этими уравнениями на рис. 1 12 построены искомые кривые w(t) и M(t), представляющие собой экспоненты.
Поиск по сайту: |
 . Характер этого движения однозначно определяется законом изменения динамического момента, который, являясь функцией моментов двигателя и нагрузки, может зависеть от скорости, времени или положения исполнительного органа.
. Характер этого движения однозначно определяется законом изменения динамического момента, который, являясь функцией моментов двигателя и нагрузки, может зависеть от скорости, времени или положения исполнительного органа.

 (1.25)
(1.25) (1.26)
(1.26)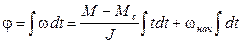

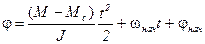 (1.27)
(1.27)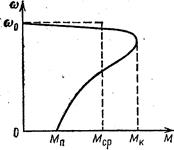
 (1.28)
(1.28)
 и Mс. с помощью (1.28) через скорость, получаем
и Mс. с помощью (1.28) через скорость, получаем (1.29)
(1.29) , найдем линейное неоднородное дифференциальное уравнение первого порядка
, найдем линейное неоднородное дифференциальное уравнение первого порядка (1.30)
(1.30) ‑ электромеханическая постоянная времени процесса, с;
‑ электромеханическая постоянная времени процесса, с; 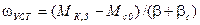 ‑ установившаяся (конечная) скорость движения, соответствующая точке 1 пересечения механических характеристик (рис. 1.10).
‑ установившаяся (конечная) скорость движения, соответствующая точке 1 пересечения механических характеристик (рис. 1.10). (1.31)
(1.31) (1.32)
(1.32) , где
, где  ‑ некоторая константа,
‑ некоторая константа,  ‑ корень характеристического уравнения
‑ корень характеристического уравнения (1.33)
(1.33) , и для свободной составляющей имеем
, и для свободной составляющей имеем (1.34)
(1.34) . Выполнив это, найдем
. Выполнив это, найдем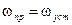 (1.35)
(1.35) (1.36)
(1.36)
 , откуда
, откуда  .
.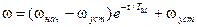 (1.37)
(1.37) (1.38)
(1.38) , предварительно подставив в него найденную зависимость w(t) из (1.37). Опуская промежуточные выкладки, приведем окончательный результат
, предварительно подставив в него найденную зависимость w(t) из (1.37). Опуская промежуточные выкладки, приведем окончательный результат (1.39)
(1.39) . В частном случае, когда
. В частном случае, когда  и
и  , эти величины могут быть определены по формулам
, эти величины могут быть определены по формулам (1.40)
(1.40)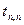 изменения скорости или момента от какого-либо начального значения до значений
изменения скорости или момента от какого-либо начального значения до значений 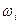 ; или Mi
; или Mi (1.41)
(1.41) , входящая в уравнения (1.37) ‑ (1.39), имеет определенное физическое содержание. Обратимся к рис. 1.11, на котором изображена идеализированная прямоугольная характеристика двигателя. Из (1.26) для определения времени разбега двигателя вхолостую до скорости w0 при
, входящая в уравнения (1.37) ‑ (1.39), имеет определенное физическое содержание. Обратимся к рис. 1.11, на котором изображена идеализированная прямоугольная характеристика двигателя. Из (1.26) для определения времени разбега двигателя вхолостую до скорости w0 при  и
и  получаем
получаем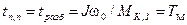 .
.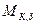 .
.
 . Иногда за практическое время переходного процесса принимается время достижения координатой 98 % установившегося значения, которому соответствует время
. Иногда за практическое время переходного процесса принимается время достижения координатой 98 % установившегося значения, которому соответствует время  .
. =0,15 кг-м2; момент нагрузки Мс неизменен и равен 50 Н×м. Механическая характеристика двигателя w(M) соответствует рис. 1.10
=0,15 кг-м2; момент нагрузки Мс неизменен и равен 50 Н×м. Механическая характеристика двигателя w(M) соответствует рис. 1.10 Для рассматриваемого примера в соответствии с (I 40)
Для рассматриваемого примера в соответствии с (I 40)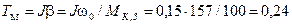
 ;
;  Н×м;
Н×м; 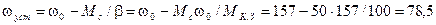 рад/с,
рад/с, 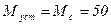 Н×м.
Н×м.
 .
.