|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Задачи для самостоятельной работы ⇐ ПредыдущаяСтр 4 из 4
1. Решить уравнения: а) в) г) 2. Вычислить 3. При каких 4. Найти действительные и мнимые части следующих выражений: а) 5. Найти множество точек, удовлетворяющих уравнению
6. Изобразить множество точек, удовлетворяющих уравнению 7. Найти множество точек, удовлетворяющих двойному неравенству 8. Изобразить на комплексной плоскости множество точек, удовлетворяющих неравенству 9. Изобразить на комплексной плоскости точки, удовлетворяющие неравенствам: а) в) 10. Записать с помощью неравенств и изобразить на комплексной плоскости следующие открытые множества точек комплексной плоскости: а) полоса, состоящая из точек, отстоящих от действительной оси на расстояние, меньшее двух единиц; б) внешность круга с центром в точке в) внутренность прямого угла, лежащего в правой полуплоскости, с вершиной в точке 11. Найти множество точек, равноудаленных 12. Изобразить на комплексной плоскости линию, заданную уравнением 13. Доказать тождество
14. Изобразить на комплексной плоскости все значения выражения 15. Найти 16. Решить уравнение Корни уравнения представить в показательной форме. 17. Решить уравнение Корни уравнения представить в алгебраической форме. 18. Доказать справедливость равенства 19. Вычислить значение функции а) б) в) г) д) е) ж) з) 20. Найти: а) 21. Доказать справедливость равенств: а) в) д) 22. Найти: а) г) 23. Найти образ точки 24. Найти образ в комплексной плоскости 25. Найти образы координатных осей Ответы 1. а) в) 2. 4. а) 5. Точки окружности 6. Множество точек параболы 7. Внутренние точки кольца с центром в точке
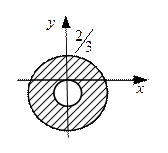
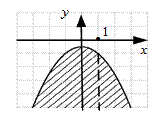
Рис. 20 Рис. 21 8. Точки, лежащие внутри области, ограниченной окружностью радиуса 1 с центром в точке (1,0) (рис. 20). 9 а) рис.21; б) рис. 22; в) рис.23.
Рис.22 Рис.23
Рис.24
Рис.25 Рис.26 11. Множество точек параболы 12. Гипербола 13. Правая ветвь гиперболы 14. Рис. 27.
7. ж) 20. а) 22. а) 24.
ОГЛАВЛЕНИЕ. КОМПЛЕКСНЫЕ ЧИСЛА........................................................3 1. Понятие комплексного числа. Алгебраическая форма комплексного числа.............................................................3 2. Тригонометрическая и показательная формы комплексного числа.......................................................................15 Произведение комплексных чисел в тригонометрической и показательной формах...................................................................18 Частное комплексных чисел в тригонометрической и показательной формах...................................................................22 Извлечение корня целой положительной степени из комплексного числа.......................................................................23 ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО...........................................................................25 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО...........................................................................28 1. Показательная функция комплексного переменного.............29 2. Логарифмическая функция комплексного переменного.......29 3. Тригонометрические функции комплексного 4. Обратные тригонометрические функции комплексного переменного...................................................................................34 5. Гиперболические функции комплексного переменного.......37 6. Обратные гиперболические функции......................................39 Задачи для самостоятельной работы...........................................40 Ответы.............................................................................................42 Учебное издание
Поиск по сайту: |
 ; б)
; б) 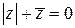 ;
;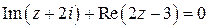 ;
;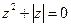 .
. , если
, если 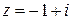 .
.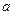 и
и 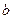 справедливо равенство
справедливо равенство  , если
, если 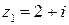 ,
,  ?
?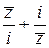 ; б)
; б) 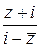 .
.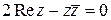 .
.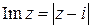 .
. .
.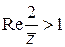 .
. ; б)
; б) 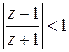 ;
;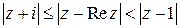 .
.
 , симметричного относительно действительной оси.
, симметричного относительно действительной оси.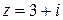 и прямой
и прямой 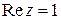 .
. ,
, 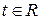 .
.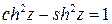 . Используя доказанное тождество, изобразить на комплексной плоскости линию, заданную уравнением
. Используя доказанное тождество, изобразить на комплексной плоскости линию, заданную уравнением (
( 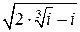 .
.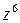 , если
, если 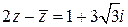 .
.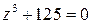 .
.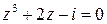 .
. .
.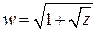 в точке
в точке  ;
;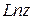 в точке
в точке 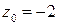 ;
;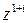 в точке
в точке  ;
;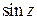 в точке
в точке  ;
; в точке
в точке  ;
; в точке
в точке  ;
;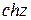 в точке
в точке 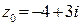 ;
;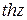 в точке
в точке 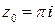 .
.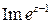 ; б)
; б) 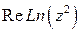 ; в)
; в) 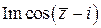 .
.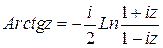 ; б)
; б) 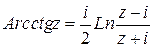 ;
;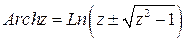 ; г)
; г) 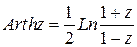 ;
;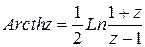 .
. ; б)
; б) 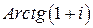 ; в)
; в) 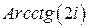 ;
;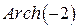 ; д)
; д)  .
.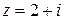 при отображении
при отображении 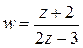 .
.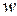 прямой
прямой 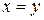 , заданной в комплексной плоскости
, заданной в комплексной плоскости 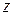 при отображении
при отображении 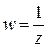 .
.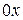 и
и 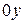 при отображении
при отображении  .
. или
или 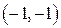 ; б)
; б) 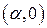 , где
, где 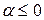 ;
; ; г)
; г) 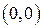 ,
, 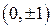 .
.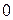 . 3.
. 3. 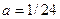 ,
, 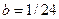 .
. ,
,  :
: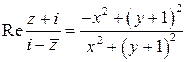 ;
; 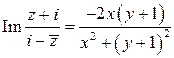 .
.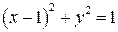 .
.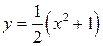 .
.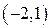 , внутренним радиусом
, внутренним радиусом  , внешним радиусом
, внешним радиусом 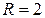 .
.

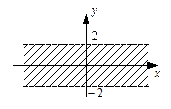 10. а)
10. а) 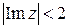 (рис.24);
(рис.24);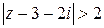 (рис.25);
(рис.25); 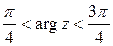 (рис.26).
(рис.26).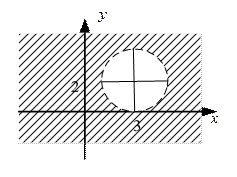
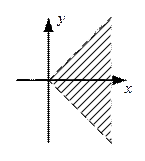
 .
.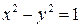 .
.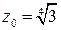 ,
, 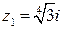 ,
, 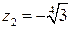 ,
, 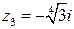 ,
,
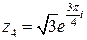 ,
, 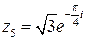 .
.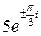 ,
, 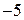 .
.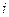 ,
,  .
.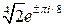 ,
, 
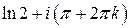 ;
;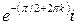 ;
; 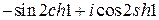
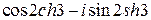 ;е)
;е) 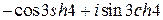 ;
;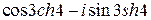 ; з)
; з) 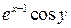 ; б)
; б) 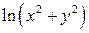 ; в)
; в)  .
.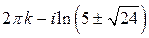 ;
; 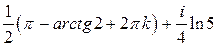 ;
; 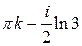 ; г);
; г);  ;
;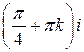 . 23.
. 23. 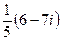 .
. . 25.
. 25.