 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Извлечение корня целой положительной степени из комплексного числа
Извлечь корень целой положительной степени Пусть
т. е. (10) - формула для извлечения корня целой положительной степени Пример 19 Представить следующие выражения в алгебраической форме: а) Решение. а) б) При при Пример 20. Решить уравнение Решение. Подставляя последовательно
(рис. 15).●
Рис. 15
ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОгоПЕРЕМЕННОго. Понятие функции комплексного переменного вводится по аналогии с понятием функции действительной переменной. Определение. Величина Это соответствие обозначается в виде Определение. Переменную Пусть Определение. Если каждому значению Определение. Множество значений Геометрически можно рассматривать
Рис. 16 Определение. Если
Рис. 17 Например, при отображении
функция Пример 21 Найти образ точки Решение. Пример 22. Найти уравнения линий в плоскости Решение.
параболы, симметричной относительно оси Подставляя Рис. 18 Пример 23. Найти образ окружности Решение 1. Так как Решение 2. Так как ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Рассмотрим некоторые элементарные функции комплексного переменного, а именно, показательную функцию
Поиск по сайту: |
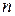 из числа
из числа 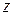 значит найти такое число
значит найти такое число  ,
,  -ая степень которого равна
-ая степень которого равна 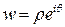 . Тогда
. Тогда 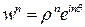 и
и 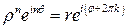 , откуда
, откуда 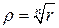 ,
, 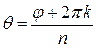 и
и 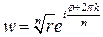
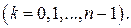 , откуда
, откуда , (10)
, (10)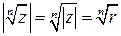 ,
,  .
. ; б)
; б) 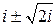 .
.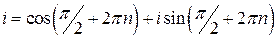 ,
, 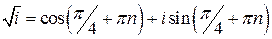 , откуда
, откуда  и
и 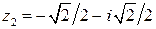 .
.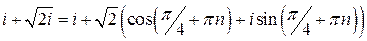

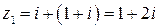 и
и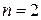
 .●
.●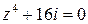 и изобразить корни этого уравнения на комплексной плоскости.
и изобразить корни этого уравнения на комплексной плоскости.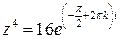


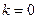 ,
, 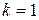 ,
, 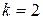 и
и 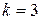 , получим четыре различных корня исходного уравнения:
, получим четыре различных корня исходного уравнения: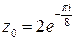 ,
, 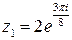 ,
,
 и
и 
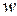 называется функцией комплексного переменного в области
называется функцией комплексного переменного в области  , если задан закон, по которому каждому значению
, если задан закон, по которому каждому значению 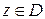 , ставится в соответствие одно или несколько значений
, ставится в соответствие одно или несколько значений 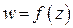 .
. .
. и
и 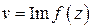 .
.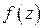 , где
, где 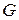 .
. (рис. 16) в некоторую область
(рис. 16) в некоторую область 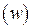 .
.
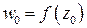 , то точка
, то точка 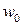 называется образом точки
называется образом точки 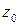 при отображении
при отображении 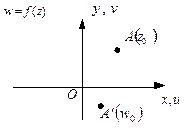 Замечание. Иногда удобно совмещать плоскости
Замечание. Иногда удобно совмещать плоскости 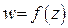 «перемещает» точку
«перемещает» точку  в точку
в точку  (рис. 17).
(рис. 17).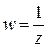 образом точки
образом точки 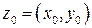 является точка
является точка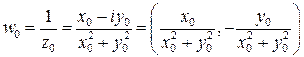 , т. е
, т. е в точку
в точку  . Очевидно,
. Очевидно,  .
.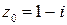 , если отображение задано формулой
, если отображение задано формулой  .
.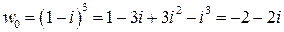 .●
.●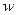 , на которые с помощью функции
, на которые с помощью функции  отображаются прямые
отображаются прямые 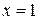 и
и 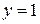 .
.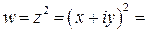 ,
, 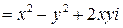 , откуда
, откуда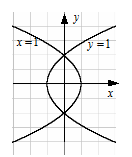
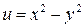 ,
, 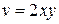 . (11) Подставляя
. (11) Подставляя 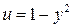 ,
, 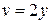 , откуда
, откуда  . Это , уравнение
. Это , уравнение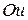 .
. ,
,  , т.е. еще одну параболу
, т.е. еще одну параболу 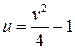 (рис. 18).●
(рис. 18).●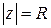 при отображении
при отображении  , т. е. образом окружности
, т. е. образом окружности 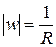 .
.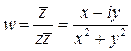 , откуда
, откуда 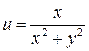
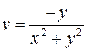 .
. ,
, 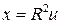 ,
,  и
и  , т.е. образом окружности
, т.е. образом окружности 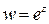 , логарифмическую функцию
, логарифмическую функцию 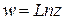 , тригонометрические -
, тригонометрические -  ,
,  ,
,  ,
, 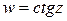 и, обратные тригонометрические функции
и, обратные тригонометрические функции 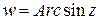 ,
, 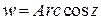 ,
,  ,
, 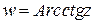 ,а также гиперболические функции
,а также гиперболические функции  ,
, 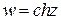 ,
, 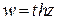 ,
, 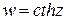 и обратные к ним функции
и обратные к ним функции 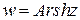 ,
, 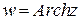 ,
,  ,
,  ).
).