 |
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
Произведение комплексных чисел в тригонометрической и показательной формах
Рассмотрим произведение двух комплексных чисел в тригонометрической и показательной формах. Пусть
Очевидно, что для сопряженных комплексных чисел имеют место следующие формулы:
Утверждение. Если
► Воспользуемся методом полной математической индукции. Доказано, что Предположим, что Тогда Следовательно, формула (7) справедлива при Следствие. Если
Формула (8) есть формула для возведения в целую положительную степень комплексного числа, заданного Из формулы (8) следует
При
Из формулы Муавра можно легко выразить Например,
Пример 16. Упростить выражение Решение.
Так как Пример 17. Найти Решение.
откуда
Частное комплексных чисел в тригонометрической и показательной формах Для комплексных чисел
Пример 18. Представить в показательной форме числа а) Решение. а) б)Найдем модуль и аргумент числа Так как действительная и мнимая части числа
Замечание. При сложении и вычитании комплексных чисел, как правило, целесообразнее использовать алгебраическую форму этих чисел. При умножении, возведении в степень и извлечении корня более рациональным может оказаться тригонометрическая или показательная форма.
Поиск по сайту: |
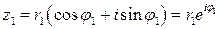 и
и 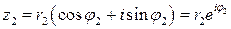 . Тогда
. Тогда 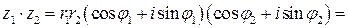
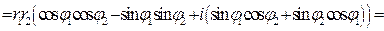
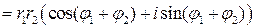 . Из последнего имеем
. Из последнего имеем 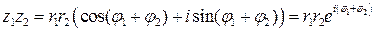 .
.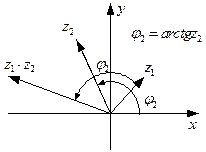 Следовательно, модуль произведения двух комплексных чисел равен произведению модулей сомножителей, а главное значение аргумента произведения с точностью до
Следовательно, модуль произведения двух комплексных чисел равен произведению модулей сомножителей, а главное значение аргумента произведения с точностью до 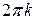 равно сумме аргументов сомножителей.
равно сумме аргументов сомножителей. 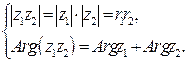 Рис. 14 Из предыдущего следует, что при геометрическом умножении комплексного числа
Рис. 14 Из предыдущего следует, что при геометрическом умножении комплексного числа 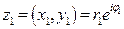 на
на 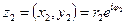 вектор
вектор  нужно повернуть вокруг начала координат на угол
нужно повернуть вокруг начала координат на угол 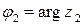 и растянуть полученный вектор в
и растянуть полученный вектор в 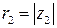 раз (рис. 14).
раз (рис. 14).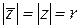 ;
; 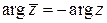 ;
; 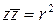 .
.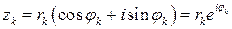
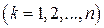 , то
, то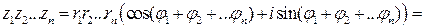
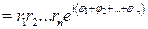 (7)
(7)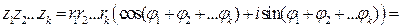
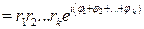 (при
(при 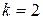 это равенство справедливо).
это равенство справедливо).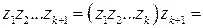
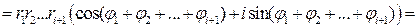
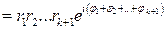 .
.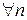 . ◄
. ◄ , то
, то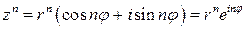 . (8)
. (8)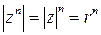 ,
,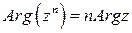 (с точностью до
(с точностью до 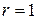 из формулы (8) получим формулу Муавра
из формулы (8) получим формулу Муавра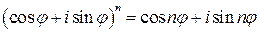 .
.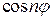 и
и 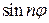 через степени
через степени 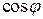 и
и 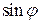 .
.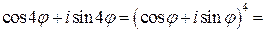
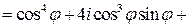
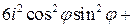
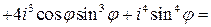
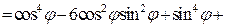
 ,
,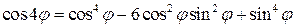 ,
,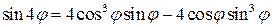
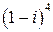 .
. .
.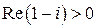 , то
, то 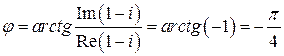 .
.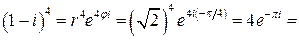
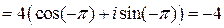 .●
.●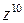 , если
, если 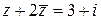 .
.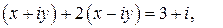
 ,
,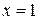 ,
,  или
или 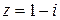 .
.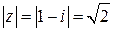 ,
, 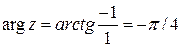 .
.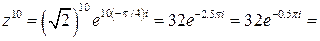
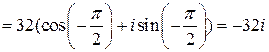 . ●
. ●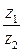
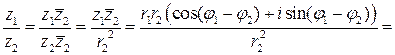
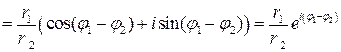 , откуда следует, что модуль частного двух комплексных чисел равен отношению модулей делимого и делителя, а главное значение аргумента частного с точностью до
, откуда следует, что модуль частного двух комплексных чисел равен отношению модулей делимого и делителя, а главное значение аргумента частного с точностью до 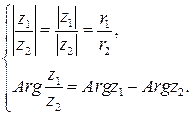 (9)
(9)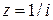 ; б)
; б)  .
.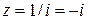 . Для этого числа
. Для этого числа 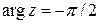 , поэтому
, поэтому  .
.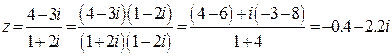 .
. 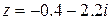 - алгебраическая форма данного числа и
- алгебраическая форма данного числа и 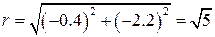 ,
, 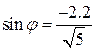 ,
, 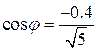 .
.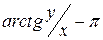 , т.е.
, т.е. 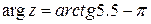 и
и .
.