|
|
|
Архитектура Астрономия Аудит Биология Ботаника Бухгалтерский учёт Войное дело Генетика География Геология Дизайн Искусство История Кино Кулинария Культура Литература Математика Медицина Металлургия Мифология Музыка Психология Религия Спорт Строительство Техника Транспорт Туризм Усадьба Физика Фотография Химия Экология Электричество Электроника Энергетика |
АРИФМЕТИЧЕСКИЕ УСТРОЙСТВА
Комбинационные устройства, которые рассматривались ранее, выполняют логические функции. Для описания их поведения используется аппарат алгебры логики. Входные и выходные сигналы оцениваются логическими 1 и 0. Дискретная техника имеет дело и с другим классом приборов, назначение которых состоит в выполнении арифметических действий с двоичными числами: сложение, вычитание, умножение, деление. К арифметическим устройствам относят также узлы, выполняющие специальные арифметические операции: выявление четности чисел и сравнение двух чисел. В этих устройствах сигналам приписываются не логические 0 и 1, а арифметические значения 0 и 1. Действия над ними подчиняются законам двоичной арифметики. Для описания работы арифметического устройства также удобно использовать таблицы истинности, как и для логических устройств. Арифметические устройства широко используются в ЭВМ и в аппаратуре информационно-измерительной техники. Важнейшая из арифметических операций – сложение (Σ). Помимо прямого назначения сложение используется и при других операциях: вычитание – это сложение, в котором вычитаемое вводится в обратном или дополнительном коде, а умножение и деление – это последовательное сложение или вычитание.
Сумматоры
Сумматоры представляют собой функциональные цифровые устройства, выполняющие операцию сложения чисел. В цифровой технике суммирование осуществляется в двоичном или, реже, в двоично-десятичном коде. По характеру действия сумматоры подразделяются на комбинационные и накопительные; по количеству одновременно обрабатываемых разрядов складываемых чисел сумматоры делятся на одноразрядные и многоразрядные. По числу входов и выходов одноразрядные двоичные сумматоры подразделяются на: – четвертьсумматоры (элементы "сумма по модулю 2"; элементы "исключающее ИЛИ"), характеризующиеся наличием двух входов, на которые подаются два одноразрядных числа, и одним выходом, на котором реализуется их арифметическая сумма; – полусумматоры, характеризующиеся наличием двух входов, на которые подаются одноименные разряды двух чисел, и двух выходов: на одном реализуется арифметическая сумма в данном разряде, а на другом – перенос в следующий (более старший разряд); – полные одноразрядные двоичные сумматоры, характеризующиеся наличием трех входов, на которые подаются одноименные разряды двух складываемых чисел и перенос из предыдущего (более младшего) разряда, и двумя выходами: на одном реализуется арифметическая сумма в данном разряде, а на другом – перенос в следующий (более старший разряд). По способу представления и обработки складываемых чисел многоразрядные двоичные сумматоры подразделяются на: – последовательные, в которых обработка разрядов чисел ведется поочередно, разряд за разрядом на одном и том же оборудовании; – параллельные, в которых слагаемые складываются одновременно по всем разрядам и для каждого разряда имеется свое оборудование. Сумматор имеет n входов разрядов слагаемого A, n входов разрядов слагаемого Ви вход переноса cr (carry – перенос). Выходами сумматора являются n выходов разрядов суммы S и выход переноса (переполнения) CR.Сумматор характеризуется четырьмя значениями задержки распространения: TcrS – от подачи входного переноса до установления всех выходов суммы при постоянном уровне на всех входах слагаемых (А и В); TAS – от одновременной подачи всех слагаемых до установления всех выходов суммы при постоянном уровне на входе переноса (выходной перенос CR не учитывается); TcrCR – от подачи входного переноса до установления выходного переноса CR при постоянном уровне на входах слагаемых; Tacr – от подачи всех слагаемых до установления выходного переноса CR при постоянном уровне на входах слагаемых. Как последовательные, так и параллельные многоразрядные сумматоры строятся на основе одноразрядных суммирующих схем.
Четвертьсумматор
Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент "сумма по модулю 2" и элемент "исключающее ИЛИ". Схема (рис. 11.1) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу ее отражает таблица истинности (табл. 11.1), а соответствующее уравнение имеет вид:
Рис. 11.1 Условное обозначение (а, б) и схема реализации четвертьсумматора (в)
На рис. 11.1 представлены условное графическое обозначение элемента и схема реализации в базисе И-ИЛИ-НЕ. Состояния четвертьсумматора при различных значениях входных сигналов представлены в таблице истинности (табл. 11.1). Здесь старшая единица, возникающая при суммировании двух единиц, не учитывается. Данный элемент выпускается в виде интегральных схем типа ЛП5 (серии 133, 155, 530, 531, 533, 555, 1531, 1533); ЛП12 (555); ЛП107 (100, 500, 1500); ЛП2 (561, 564); ЛП14 (1561) и т. п.
Полусумматор
Полусумматор (рис. 11.2) имеет два входа a и b для двух слагаемых и два выхода: S сумма и CR (или P) – перенос. Обозначением полусумматора служат буквы HS (half sum – полусумма). Два одноразрядных числа при сложении в двоичной системе дают такие результаты:
Таблица 11.2
b
Эти результаты можно представить в виде таблицы (табл. 11.2). В соответствии с таблицей работу полусумматора можно описать следующими уравнениями:
Рис. 11.2. Условное обозначение (а) и схема реализации полусумматора (б)
Уравнения показывают, что выражение для выхода S и столбец таблицы истинности совпадают с уравнениями и таблицей, описывающими работу элемента исключающее ИЛИ, а для выхода Р – с уравнением и таблицей элемента И. Условное графическое обозначение и логическая структура полусумматора представлены на рис. 11.2. Полусумматор используется, обычно, только для суммирования младших разрядов многоразрядных двоичных чисел.
Поиск по сайту: |
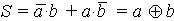
 Таблица 11.1
Таблица 11.1 а
а 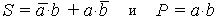 (2)
(2)